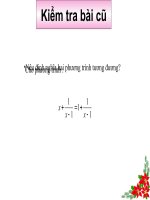- Toán học 9 - Bùi Hà Thanh - Website của Trường THCS Tam Hưng - Thanh Oai
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.02 MB, 22 trang )
<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>
<b>KIỂM TRA BÀI CŨ </b>
<b> </b>
<b>a.Viết hệ thức viét</b>
<b>b. Áp dụng : Giải phương trình</b>
</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>
<b>a. Hệ thức viét</b>
<b>:</b>
<b>Phương trình : a x</b>
<b>2</b><b> + b x + c = 0</b>
<b><sub> ( a </sub></b>≠
<b><sub> 0 )</sub></b><b>Có hai nghiệm : x<sub>1</sub> + x<sub>2</sub> =- b/a</b>
<b> x<sub>1</sub> .x<sub>2</sub> =c/a</b>
<b>+> Nếu a+b+c=0 suy ra PT có x<sub>1</sub> =1 ;x<sub>2</sub> = c/a</b>
<b>+>Neáu a – b +c=0 suy ra PT có x<sub>1</sub> =-1 ;x<sub>2</sub> = -c/a </b>
<b>b. Áp dụng : Giải phương trình</b>
<b> </b>
<b>x</b>
<b>2</b><b> – </b>
<b>4</b>
<b> x + 3 = 0</b>
<b>Ta coù : a + b + c = 1 + (-4)+3 =0</b>
<b>Suy ra PT có hai nghiệm x<sub>1</sub>=1 ;x<sub>2</sub>=3</b>
</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>
<b>Làm cách nào để giải được </b>
<b> phương trình</b>
<b>: </b><b> </b>
</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4></div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5></div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>
<i><b>a</b></i>
<i><b>.Định Nghóa:</b></i>
<i><b> </b></i>
<i><b>PT trùng phương là PT có dạng</b></i>
</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7></div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>
<b>b.Nhận xét</b>
.
-
Phương trình trên không phải
là phương trình bậc hai,song có
thể đưa nó về phương trình bậc
hai bằng cách
<b>đặt ẩn phụ</b>
.
Chẳng hạn đặt x
2= t thì ta được
phương trình bậc hai :
</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>
<i><b>x</b></i>
<i><b>4</b></i><i><b> – 5x</b></i>
<i><b>2</b></i><i><b> + 4 = 0</b></i>
<b>Đặt ẩn phụ t = x2 0, ta có phương trình:</b>
<b> t2 - 5t + 4 = 0 ( </b><i><b>a =1, b = -5, c = 4</b></i><b> )</b>
<b>coù daïng a + b + c = 1 -5 + 4 = 0</b>
<b>Phương trình có 2 nghiệm: t<sub>1</sub> = 1 </b><i><b>(nhaän)</b></i><b>, t<sub>2</sub>= = 4 </b><i><b>(nhaän)</b></i>
<b> t = x2 = 1 </b><sub></sub><b> x = 1 ; x = -1</b>
<b> t = x2 = 4</b><sub></sub><b> x = 2 ; x = -2</b>
Giải phương trình :
<i><b>KL: phương trình có nghieäm : x</b><b><sub>1</sub></b><b>=1 ; x</b><b><sub>2</sub></b><b>=-1;</b></i>
<i><b> x</b><b><sub>3</sub></b><b>=2 ; x</b><b><sub>4</sub></b><b>=-2</b></i>
c.Ví Dụ 1
</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>
<b>1.Giải các phương trình </b>
<b>trùng phương sau:</b>
<b>a) 4x</b>
<b>4</b><b> + x</b>
<b>2</b><b> -5=0</b>
</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>
• <i><b>a) 4x</b><b>4</b><b> + x</b><b>2</b><b> – 5 = 0</b></i>
• đặt ẩn phụ t = x2 0, ta có phương trình:
• 4t2 + t - 5 = 0 ( <i>a =4, b = 1, c = -5</i> )
• có dạng a + b + c = 0 => t1 = 1 <i>(nhận)</i>,
• t2 = -5/4 <i>(loại)</i>
• Với t = x2 = 1 <sub></sub> x<sub>1</sub> =1; x<sub>2</sub> = -1
• -KL: phương trình trùng phương có 2 nghiệm:
• x1 = 1 ; x2 = -1
</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>
<i><b>b. 3x</b><b>4</b><b> + 4x</b><b>2</b><b> + 1 = 0</b></i>
• Đặt ẩn phụ t = x2 0, ta có phương trình:
• 3t2 + 4t + 1 = 0 ( <i>a =3, b = 4, c = 1</i> )
• Có dạng a - b + c = 3 – 4 + 1 = 0
• phương trình có 2 nghiệm: t1 = -1<i>(loại)</i>,
• t2 = -1/3 <i>(loại)</i>
• KL: phương trình trùng phương vô nghiệm.
</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13></div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>
<i><b>Các bước giải phương trình chứa ẩn ở </b></i>
<i><b>mẫu.</b></i>
<i><b>Bước 1</b></i><b>: Tìm điều kiện xác định của phương trình</b>
<i><b>Bước 2</b></i><b>: Quy đồng mẫu hai vế của phương trình rồi khử </b>
<b> maãu</b>
<i><b>Bước 3</b></i><b>: Giải phương trình vừa nhận được</b>
<i><b>Bước 4</b></i><b>: Kết luận.Trong các giá trị của ẩn tìm được ở </b>
</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15>
<b> </b>
<b>2</b>
<b>.Giaûi</b>
<b> phương trình sau:</b>
2
2
3
6
1
</div>
<span class='text_page_counter'>(16)</span><div class='page_container' data-page=16>
-Điều kiện: x ………và x …….
≠
≠
-Khử mẫu và biến đổi ta có phương
trình:
• x2 – 3x + 6 = ………..
x2 – 4x + 3 = 0 phương trình
có dạng gì? x<sub>1</sub>= ….. . x<sub>2</sub> = ………
x1 có thỏa mãn ĐK nói trên không,
</div>
<span class='text_page_counter'>(17)</span><div class='page_container' data-page=17>
• Giải
• Điều kiện: x ± 3≠
• Ta có phương trình:
• x2 – 3x + 6 = x + 3
x2 – 4x + 3 = 0 ( <i>a =1, b = -4, c = 3</i> )
coù daïng a + b + c = 1 -4 + 3 = 0
Phương trình có 2 nghiệm:
x1 = 1 <i>(nhận)</i>, x2 = 3 <i>(loại)</i>
</div>
<span class='text_page_counter'>(18)</span><div class='page_container' data-page=18></div>
<span class='text_page_counter'>(19)</span><div class='page_container' data-page=19>
<b>Thế nào là phương trình </b>
<b>tích.</b>
</div>
<span class='text_page_counter'>(20)</span><div class='page_container' data-page=20>
• Phương trình tích là phương trình có dạng
• A(x).B(x) = 0.
• * Cách giải phương trình tích?
• p dụng cơng thức: A(x).B(x) = 0
• A(x) = 0 hoặc B(x) = 0
• Giải phương trình A(x) = 0 và B(x) = 0, rồi
</div>
<span class='text_page_counter'>(21)</span><div class='page_container' data-page=21>
<i><b> </b><b>(x+1).( x</b><b>2</b><b> + 2x-3) = 0</b></i>
<b>Giaûi:</b>
<b> (x+1).(x2 + 2 x -3) = 0</b>
<b> x + 1 = 0 Hoặc x2 + 2 x -3 =0</b>
<b> * x + 1 =0 </b><b> x = -1</b>
<b> * x2 + 2 x -3 = 0 </b><sub></sub><b> x =1 ; x =-3</b>
Giải phương trình :
<i><b>KL: phương trình có các nghiệm : x</b><b><sub>1</sub></b><b>=-1 ; x</b><b><sub>2</sub></b><b>=1;</b></i>
<i><b> x</b><b><sub>3</sub></b><b>= -3 </b></i>
</div>
<span class='text_page_counter'>(22)</span><div class='page_container' data-page=22>
<b>Hướng dẫn làm việc ở nhà</b>
<b>Xem trước bài Giải bài tốn </b>
<b>Phần luyện tập</b>
<b>1.Giải phương trình:</b>
<b>1) x</b>
<b>4</b><b> </b>
<b> - 5x + 4 = 0</b>
<b> </b>
<b>2) 2 x</b>
<b>4 </b><b> - 3x</b>
<b>2</b><b> - 2 = 0</b>
<b> </b>
<b>3) 3x</b>
<b>4</b><b> + 10x</b>
<b>2</b><b> + 3 = 0</b>
</div>
<!--links-->