Bài tập mạch điện 2
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (372.44 KB, 22 trang )
1
U
1
I
O
x
3
U
3
I
l
l/2
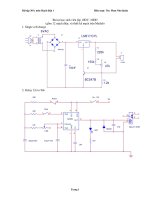
Bài tập: Mạch Điện 2
Bài 1:
Cho đường dây với các thông số sau:
0
-3
0
-9
0
6
0
1
l = 100 km
R = 6 /m
L = 1,6.10 H/km
C = 6,4.10 F/km
G = 10 S/km
f = 100 Hz
U = 1 kV
0
1
I = 500 -15 A
1/ Xác định các hệ số:
C
, Z , V,
2/ Xác định U và hệ số phản xạ sóng giữa đường dây
Giải:
a/Ta có:
2 f 2. .100 200 (rad/s)
o o o
-6 -6
o o o
oo
Z R j L = 6 + j ( )
Y G j C 10 +4,0212.10 j (S)
Z .Y 0,0037 + 0,0034j (1/km)
= 0,0037 (neper/km)
= 0,0034
(rad/km)
o
C
o
5
3
Z
Z 1013,2 - 664,56j ( )
Y
V= 1,8428.10 (km/s)
V
= 1,8428.10 (km)
f
b/ Ta có:
54
1 1 C 1
54
2 1 C 1
1
A U Z .I 2,8816.10 - 9,4922.10 j
2
1
A U Z .I -2,8716.10 9.4922.10 j
2
Mặc khác:
xx
x 1 2 x x
xx
12
x x x
CC
U A .e A .e U U
AA
I .e .e I I
ZZ
Tại điểm: x = l/2 thì
.l/2 .l/2
3 l/2 1 2 l/2 l/2
54
U U A .e A .e U U
-1,3683.10 - 6,4567.10 j (V)
-136,83 - 64,567j (kV)
.l/2 .l/2
12
3 l/ 2 l/2 l/2
CC
AA
I I .e .e I I
ZZ
479,95 144,69j (A)
1
U
1
I
O
x
2
U
2
I
l
c
Z
Bài 2:
c
-3
2
l 30 km
Z 500
=3.10 Neper/km
Z 500
GTHD của điẹn áp ở dầu đường dây là U
1
= 120V
a/ Xác định GTHD của U
2
;I
2
cuối đường dây
b/ Xác định hiệu suất truyền tải
của đường dây.
Giải:
a/ Do:
cc
ZR
đường dây gần như vận hành ở chế đọ hoà hợp tải nên:
0
. Tức
là mọi điểm trên đường dây chỉ có ST mà không có SPX
Xây dựng công thức theo hệ trục như hình vẽ:
x x x
x 1 2 x x x x 1
x x x
1 2 1
x x x x x
C C C
U A .e A .e U U U U A .e
(1)
A A A
I .e .e I I I I .e
Z Z Z
Ta có
.0
1 (x 0) (x 0) 1 1
11
U U U A .e A
UA
U
1
1
j.
1 1 U 1 1
U U U .e A (2)
Thế (2) vào (1) ta được:
U
1
U
1
U
1
U
1
U
1
U
1
j.
( j )x
x1
j.
( j )x
1
x
C
j( x)
x
x1
j( x)
x
1
x
C
j( l)
l
2 (x l) 1
j( l)
l
1
2 (x l)
C
l (30.
21
U U .e .e
U .e
I .e
Z
U U .e e
U
I .e e
Z
U U U .e e
U
I I .e e
Z
U U .e 120.e
3
3
3.10 )
l (30.3.10 )
1
2
C
109.6717 (V)
U
120
I .e .e 0.2193 (A)
Z 500
b/ Hiệu suất truyền tải
:
Ta có
2
1
P
.100%
P
Với:
22
11
2 2 2 U I
1 1 1 U I
P U .I .cos( )
P U .I .cos( )
Chế độ hoà hợp tải nên:
11
22
1 1 1 1
2 2 2 2
11
cc
11
22
cc
22
11
22
UI
UI
U U ; I I
U U ; I I
UU
ZR
II
UU
ZR
II
U ;I cu`ng pha
U ;I cu`ng pha
cos( ) 1
cos( ) 1
l
11
21
.0
l
11
1
1 (x 0)
2
CC
C
ll
1
1
C
22
1
11
1
C
2l
U A 120
U U .e
;
AU
U
I I .e
I .e
ZZ
Z
U
U .e . .e
Z
U .I
.100% 100%
U
U .I
U.
Z
e .100%
85%
1
U
1
I
O
x
2
U
2
I
l
2
Z
Bài 3:
Cho đường dây không tiêu tán có:
3
2(t)
l 100 km
3,4.10 rad/ km
U 110 2 sin( t) kV
Xác địng U
2(t)
ở đầu đường dây trong các trường hợp có:
a/ Z
2
= Z
c
b/ Z
2
= 0,5Z
c
Giải:
Ta có:
x 2 2 c
2
x2
c
U U cos x jI Z sin x
U
I I cos x j sin x
Z
Mà
2
2
2
U
I
Z
nên:
c
x 2 2 (x) (x)
2
2
2
c
x
2
cc
(x)
22
Z
U U cos x j sin x U .M
Z
Z
M cos x sin x
Z
ZZ
sin x
arctan arctan tan x
Z cos x Z
a/
c
2C
2
Z
Z = Z 1
Z
22
x
(x)
M cos x sin x 1
sin x
arctan arctan tan x
cos x
1 (x l)
1 (x l)
1 2 1 1
1(t)
M M 1
arctan tan l 0,34 (rad)
U U .M 110.1 0,34 110 0,34
U 110 2 sin( t 0,34) (kV)
b/
c
2C
2
Z
Z = 0,5.Z 2
Z
2
2 2 2
x
(x)
M cos x 2sin x cos x 4sin x
sin x
arctan 2. arctan 2.tan x
cos x
22
1 (x l)
1 (x l)
1 2 1 1
1(t)
M M cos l 4sin l 1,915
arctan tan l 0,616 (rad)
U U .M 110.1,915 0.6157 210,62 0,616
U 210,62 2 sin( t 0,616 ) (kV)
L
1
I
O
x
2
U
2
I
l
1
U
1
V
Z
Bài 4:
Một đường dây không tiêu tán. Có chiều dài l, Z
C
= R
C
, dòng điện có tần số f,
tải cuối đường dây là cuộn cảm L.
Xác định L để hệ đường dây và tải trở thành mạch cộng hưởng áp
Giải:
1
(x)
1
V
1
x 2 2 c
2
x2
c
2 L 2
x 2 L c
L
x2
c
Lc
V
L
c
U
Z
I
U U cos x jI Z sin x
U
I I cos x j sin x
Z
U j.X .I
U j.I X cos x Z sin x
X
I I cos x sin x
Z
X cos x Z sin x
Zj
X
cos x sin x
Z
1
1
Lc
L
c
Lc
V
L
c
V
Lc
Lc
c
X Z tan x
j
X
1 tan x
Z
X Z tan l
Zj
X
1 tan l
Z
Z0
X Z tan l 0
X Z tan l
Z
L tan l
2. .f