định lý talet
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (850.36 KB, 16 trang )
1. Cho hình vẽ. Biết các đường thẳng a, b, c, d song song
cách đều. Em có kết luận gì về độ dài các đoạn thẳng EF,
FG,GH?
a
b
c
d
m
E
F
G
H
Kiểm tra kiến thức cũ
2. Tỉ số của hai số là gì? Cho a = 3 và b = 5, em hãy viết tỉ số
của hai số a và b?
EF, FG, GH là các đoạn chắn trên đoạn EH
1.Tỉ số của hai đoạn thẳng:
EF
MN
=
4
7
?
Chú ý:
Tỉ số của hai đoạn thẳng không phụ thuộc vào cách
chọn đơn vị đo.
Tỉ số của hai đoạn thẳng luôn là số dương
?
EF=0,4dm; MN=7cm.
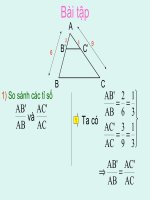
Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ (hình vẽ sau)
D’
C’
D
C
A’ B’
A B
So sánh các tỉ số
AB
CD
và
A’B’
C’D’
?
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
''
''
3
2
6
4
''
''
3
2
DC
BA
CD
AB
DC
BA
CD
AB
=⇒
==
=
Ta có
Ta nói AB và CD tỉ lệ với A’B’ và C’D’
?
Vẽ tam giác ABC trên giấy kẻ ngang
(hình dưới). Dựng đường thẳng a
song song với cạnh BC, cắt hai
cạnh AB, AC theo thứ tự tại B’ và C’.
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
C
B
A
a
C'B'
Hãy so sánh các tỉ số sau?
AB' AC'
AB AC
và
B'B C'C
AB AC
và
AB' AC'
B'B C'C
và
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
C
B
A
a
C'B'
AC
AC'
AB
AB'
?
AC
AC'
?
AB
AB'
⇒
=
=
?
CC'
AC'
BB'
AB'
?
CC'
AC'
?
BB'
AB'
⇒
=
=
?
AC
CC'
AB
BB'
?
AC
CC'
?
AB
BB'
⇒
=
=
?
AC
AC'
AB
AB'
8
5
AC
AC'
8
5
AB
AB'
=⇒
=
=
CC'
AC'
BB'
AB'
3
5
CC'
AC'
3
5
BB'
AB'
=⇒
=
=
AC
CC'
AB
BB'
8
3
AC
CC'
8
3
AB
BB'
=⇒
=
=
Định lí Ta-lét.
Nếu một đường thẳng song song với một cạnh của tam giác
và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những
đoạn thẳng tương ứng tỉ lệ.
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
3. Định lí Ta-lét trong tam giác
Trong các trường hợp sau, trường hợp nào thỏa mãn định
lý Ta-lét?
j
m
x
x // NO
TH3
75°
75°
TH2
TH1
80°
60°
T
E
D
A
B
C
FG
H
M
N
O
K
F
E
a
N
M
D
a
C'
B'
? Từ hình vẽ ta có tỉ số nào bằng
nhau?
MN// DE
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
DM DN
DE DF
=
DM DN
ME NF
=
ME NF
DE DF
=
3. Định lí Ta-lét trong tam giác
Giải:
?
Tính độ dài x ở hình vẽ dưới:
E
D
B
A
C
10
x
5
3
a
a//BC
Vì a//BC nên DE//BC, theo địnhLí ta-lét ta có:
105
3 x
hay
EC
AE
DB
AD
==
32
5
10.3
==
x
suy ra:
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
3. Định lí Ta-lét trong tam giác
4.Áp dụng
Giải:
Tính độ dài y ở hình bên:
C
A
B
D
E
4
5
3,5
y
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
3. Định lí Ta-lét trong tam giác
4.Áp dụng
Vì DE và BA cùng vuông góc với CA Nên DE//BA, theo định
lí Ta-lét ta có:
Suy ra:
y
hay
CA
CE
CB
CD 4
5,35
5
=
+
=
8,6
5
5,8.4
==
y
45
°
Sơ lược về cuộc đời
Nhìn lại lòch sử phát triển
của toán học, người ta có thể
xem Talét là một trong
những nhà hình học đầu tiên
của Hi Lạp.Talét sinh vào
khoảng năm 624 và mất vào
khoảng 547 trước công
nguyên,tại thành phố Milê-
một thành phố giàu có nhất
thời cổ Hi Lạp,
Talét đã giải được một bài
toán đo chiều cao của một
kim tự tháp Ai Cập bằng
một phương pháp hết sức
đơn giản.Lòch sử kể lại rằng
Talét đo được chiều cao của
tháp đó nhờ áp dụng tính
chất của tam giác đồng dạng.
Ông đã chọn đúng thời điểm
khi các tia nắng mặt trời tạo
với mặt đất một góc 45
0
Tức là khi độ dài bóng của
một vật đặt thẳng đứng trên
mặt đất bằng chính chiều cao
của vật đó.
1. Tỉ số của hai đoạn thẳng:
2. Đoạn thẳng tỉ lệ: AB,CD tỉ lệ với A’B’,C’D’
3. Định lí Ta - Lét trong tam giác:
AB a
CD b
=
' '
' '
AB A B
CD C D
⇔ =
Nếu một đường thẳng song song với một cạnh của tam giác và cắt
hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng
tương ứng tỉ lệ.
GT ∆ABC; B’C’//BC(B’ AB,C’ AC)
KL
' ' ' ' ' '
; ;
' '
AB AC AB AC B B C C
AB AC B B C C AB AC
= = =
∈
∈
a
C'
B'
CB
A
5. Hướng dẫn về nhà
Hướng dẫn bài 4/59 SGK
Áp dụng tính chất của tỉ lệ thức để
giải bài tập 4
Về nhà cần học thuộc định lí Ta-lét . Làm bài tập số 1,2,3,4,5b
trang 58, 59 SGK. Đọc trước bài định lí đảo và hệ quả của
định lí Ta lét.
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
3. Định lí Ta-lét trong tam giác
4.Áp dụng
Giải :
Vì MN//BC, theo định lí ta-lét
ta có:
55,8
54
−
==
x
hay
NC
AN
MB
AM
8,2
5
5,3.4
==
x
Suy ra:
? Tính x trong trường hợp sau
B
A
C
M N
4
x
5
8,5
a) MN//BC
1.Tỉ số của hai đoạn thẳng:
2.Đoạn thẳng tỉ lệ
3. Định lí Ta-lét trong tam giác
4.Áp dụng