SỞ GD &ĐT VĨNH PHÚC
TRƯỜNG THPT NGUYỄN THÁI HỌC

BÁO CÁO KẾT QUẢ
NGHIÊN CỨU, ỨNG DỤNG SÁNG KIẾN

Bài toán cực trị của hàm số chứa
dấu giá trị tuyệt đối
Tác giả: Hoàng Thị Hiền
Mã môn: 52

Năm học 2019 -2020

1


SỞ GD &ĐT VĨNH PHÚC
TRƯỜNG THPT NGUYỄN THÁI HỌC

BÁO CÁO KẾT QUẢ
NGHIÊN CỨU, ỨNG DỤNG SÁNG KIẾN

Bài toán cực trị của hàm số chứa
dấu giá trị tuyệt đối
Tác giả: Hoàng Thị Hiền
Mã môn: 52

Năm học 2019 -2020

2

BÁO CÁO KẾT QUẢ
NGHIÊN CỨU, ỨNG DỤNG SÁNG KIẾN
1. Lời giới thiệu
Trong chương trình toán phở thơng, dạng bài tốn: Bài toán cực trị của hàm
số chứa dấu giá trị tụt đới là một trong các dạng bài tốn địi hỏi tư duy đối
với học sinh THPT và thường gặp trong các đề thi đại học.
Nhằm giúp các em học sinh nắm vững phương pháp xác định và tính cực trị
của hàm số chứa dấu giá trị tuyệt đối vận dụng kiến thức đó vào giải bài toán.
Giúp học sinh phát triển năng lực tư duy sáng tạo, năng lực tư duy thuật giải.
Đồng thời góp phần nâng cao hiệu quả giáo dục và góp phần nâng cao chất
lượng giảng dạy môn toán ở trường trung học phổ thông tôi chọn đề tài:
“Bài toán cực trị của hàm số chứa dấu giá trị tuyệt đối”.
2. Tên sáng kiến:
“Bài toán cực trị của hàm số chứa dấu giá trị tuyệt đối”.
3. Tác giả sáng kiến:
- Họ và tên tác giả: Hoàng Thị Hiền
- Địa chỉ tác giả: Trường THPT Nguyễn Thái Học
- Số điện thoại:01668804899

E_mail:

4. Chủ đầu tư tạo ra sáng kiến
5. Lĩnh vực áp dụng sáng kiến: Sáng kiến có thể áp dụng vào giảng dạy cho
học sinh lớp 12 THPT
6. Ngày sáng kiến được áp dụng lần đầu hoặc áp dụng thử: Tháng 10 năm
2019
7. Mô tả bản chất của sáng kiến:
7.1. Về nội dung của sáng kiến:


3


CHƯƠNG I: CƠ SỞ LÝ LUẬN VÀ THỰC TIỄN
BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ CHỨA DẤU GIÁ TRỊ TUYỆT ĐỚI
Phần I. CƠ SỞ LÝ THÚT.
1.Các phép biến đổi đờ thị
a.Các phép tịnh tiến đờ thị
Cho hàm số
có đồ thị (C). Khi đó, với số thực a > 0 ta có:
 Hàm số
có đồ thị (C’) là tịnh tiến của (C) theo phương của trục Oy
lên trên a đơn vị.
 Hàm số
có đồ thị (C’) là tịnh tiến của (C) theo phương của trục
Oy xuống dưới a đơn vị.
 Hàm số
có đồ thị (C’) là tịnh tiến của (C) theo phương của trục Ox
qua trái a đơn vị.
 Hàm số
có đồ thị (C’) là tịnh tiến của (C) theo phương của trục Ox
qua phải a đơn vị.
b. Các phép biến đổi đờ thị khác
Cho hàm số
có đồ thị (C). Khi đó, với số a > 0 ta có:
 Hàm số

có đồ thị (C’) là đối xứng của (C) qua trục Ox.

 Hàm số


có đồ thị (C’) là đối xứng của (C) qua trục Oy.

 Hàm số
có đồ thị (C’) bằng cách:
- Giữ nguyên phần đồ thị (C) nằm bên phải trục Oy (cả những điểm nằm
trên trục Oy)
- Bỏ phần đồ thị của

nằm bên trái trục Oy.

- Lấy đối xứng phần đồ thị

nằm bên phải trục Oy qua trục Oy.

 Hàm số
có đồ thị (C’) bằng cách:
- Giữ nguyên phần đồ thị (C) nằm phía trên trục Ox (cả những điểm nằm
trên Ox)
- Lấy đối xứng phần đồ thị (C) nằm phía dưới trục Ox qua trục Ox
- Bỏ phần đồ thị của (C) nằm dưới trục Ox.
2. Khái niệm cực trị của hàm số
Giả sử hàm số f (x) xác định trên tập hợp D và x0 D
+ x0 là điểm cực tiểu của hàm số f(x) nếu tồn tại một khoảng (a;b) chứa x 0
sao cho (a;b)  D và

4


+ x0 là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b) chứa x0

sao cho (a;b)  D và
PHẦN II : NỘI DUNG
DẠNG 1: CÁC BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ
Để giải quyết các bài toán cực trị của hàm số
ba cách sau:

ta có dùng một trong

Cách 1: Lập bảng biến thiên của hàm số
Cách 2: Sử dụng phép biến đởi đờ thị
Ta có
Từ đờ thị
suy ra đồ thị
bằng cách:
+ Giữ nguyên phần đồ thị của (C) ở phía trên trục hoành (kể cả những
điểm nằm phía trên trục hoành).
+ Lấy đối xứng phần đồ thị của (C) ở phía dưới trục hoành qua trục
hoành.
+ Bỏ phần đồ thị của (C) phía dưới trục hoành.
Cách 3: Sử dụng kết quả của nhận xét sau:
Nhận xét 1:
Gọi k là số điểm cực trị của hàm số y = f(x); h là số nghiệm đơn của
phương trình f(x) = 0; e là số nghiệm bội lẻ của phương trình f(x) = 0,
thì số điểm cực trị của hàm số
bằng k + h + e
Để chứng minh nhận xét trên, trước tiên ta chứng minh bổ đề sau:
Bổ đề: Nếu
là điểm tới hạn của hàm số y = f(x) thì
của hàm số g(x)=| f(x)|
Chứng minh bổ đề:


cũng là điểm tới hạn

+ Ta có
+ Theo giả thiết,

là điểm tới hạn của hàm số

nên

xác định và

khơng xác định.
+) Ta có
xác định. Vậy

. Vì

xác định nên

xác định. (*)

5


+ Ta có

. Vì
khơng xác định. Vậy


khơng xác định nên

khơng xác định.(**)

Từ (*), (**) suy ra cũng là điểm tới hạn của hàm số g(x)=| f(x)|
Chứng minh nhận xét 1
Thật vậy
+ Theo giả thiết, y = f(x) có k điểm cực trị
nghiệm bội lẻ và t điểm tới hạn mà m + n + t = k. (*)
+ Theo giả thiết, h là số nghiệm đơn của phương trình
bội lẻ của phương trình
+

có m nghiệm đơn, n
; e là số nghiệm

(**)

;

Theo (*), (**) ta có số điểm cực trị của hàm số

bằng k + h + e

Nhận xét 2: Số điểm cực trị của hàm số
bằng số điểm cực trị
của hàm số y = f(x).
Thật vậy
+) Theo giả thiết y = f(x) có k điểm cực trị
có m nghiệm đơn, n

nghiệm bội lẻ và t điểm tới hạn mà m + n + t = k. Giả sử các nghiệm đó là
+)

có

;

có k giá trị
(gồm nghiệm đơn, nghiệm bội lẻ, điểm tới hạn). Vậy
có k điểm
cực trị.
Hay số điểm cực trị của hàm số
bằng số điểm cực trị của hàm số
y = f(x).
1.1.Bài toán cơ bản: “Cho hàm số

. Hỏi số điểm cực trị của hàm số

”

6


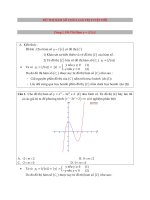
Bài 1:
Cho hàm số

có đồ thị (C) như hình vẽ. Tìm số điểm

cực trị của hàm số
Lời giải

Cách 1:

Từ đồ thị (C) ta suy ra đồ thị (C’) của hàm số
(theo phép suy ra đồ thị )

Nhìn đồ thị (C’), ta thấy hàm số
có 5 điểm cực trị
Cách 2:
+ Hàm số y = f(x) có 2 điểm cực trị
+ Phương trình f(x) = 0 có 3 nghiệm đơn
+ Phương trình f(x) = 0 có 0 nghiệm bội lẻ
Vậy số điểm cực trị của hàm số
bằng 2 + 3 + 0 = 5
Bài 2: Cho hàm số

có đồ thị (C) như hình vẽ. Tìm

số điểm cực trị của hàm số
Lời giải
Cách 1:
Từ đồ thị (C) ta suy ra đồ thị (C’) của hàm số
Nhìn đồ thị (C’) , ta thấy hàm số có 5 điểm cực trị.
Cách 2:
+ Hàm số y = f(x) có 3 điểm cực trị.
Phương trình f(x) = 0 có 2 nghiệm đơn.
Phương trình f(x) = 0 có 0 nghiệm bội lẻ .
Vậy số điểm cực trị của hàm số

bằng 3 + 2 + 0 = 5.


Bài 3:
Cho hàm số

có bảng biến thiên

như hình vẽ. Đồ thị hàm số
bao nhiêu điểm cực trị?

x
y’
y

có

+

-1
0
5

-

3
0

+

1

Lời giải + Đờ thị hàm số y = f(x) có 2 điểm cực trị.

+ Phương trình f(x) = 0 có 1 nghiệm đơn.
+ Phương trình f(x) = 0 có 0 nghiệm bội lẻ.
Vậy số điểm cực trị của hàm số 2 + 1 + 0 = 3.
7


Bài 4: Cho hàm số

có bảng biến thiên như hình vẽ. Đồ thị hàm số

có bao nhiêu điểm cực trị ?
x
y’
y

-1
0

-

+

0
0
3

1
0

-


0

+

0

Lời giải
+ Đồ thị hàm số y = f(x) có 3 điểm cực trị.
+ Phương trình f(x) = 0 có 0 nghiệm đơn (Phương trình f(x) = 0 có 2 nghiệm bội chẵn)
+ Phương trình f(x) = 0 có 0 nghiệm bội lẻ.
Vậy số điểm cực trị của hàm số
Bài 5: Hàm số
Lời giải

Xét
+

là 3 + 0 + 0 = 3.

có bao nhiêu điểm cực trị?

có
x
y’
y

-

0


0
0
3

+

-

-1
+ Hàm sớ

Bài

+

-1

có 3 điểm cực trị.

+ Phương trình
+ Phương trình
số

0

có 4 nghiệm đơn.
có 0 nghiệm bội lẻ Suy ra số điểm cực trị của hàm
là 3 + 4 + 0 = 7.


6: Tính tổng các giá trị cực đại của hàm số

Lời giải

Xét

có
x
y’

-

0

+

0
0

-

0

+
8


y

-2

-6

+ Hàm số
+ Phương trình

-6

có 3 điểm cực trị.
có 2 nghiệm đơn.

+ Phương trình

có 0 nghiệm bội lẻ.

Suy ra, số điểm cực trị của hàm số

là 5.

Các điểm cực đại của đồ thị hàm số là A(

;6), B(

Tổng các giá trị cực đại của hàm số

là 12.

Bài 7: Biết đồ thị hàm số
Hàm số
Lời giải


cắt trục hoành tại đúng 2 điểm.
có bao nhiêu điểm cực trị?

+ Vì đồ thị hàm số

cắt trục hoành tại đúng 2 điểm nên căn cứ

vào hình dáng đồ thị ta thấy hàm số
+

Mặt

;6).

có hai điểm cực trị

khác

.

Do

đó

phương

.
trình

có 1 nghiệm đơn và 1 nghiệm kép.

Vậy số điểm cực trị của hàm số
Bài

8: Biết đồ thị hàm số

bằng 2 + 1 = 3.
có hai điểm cực trị nằm về hai phía

so với trục hồnh. Số điểm cực trị của hàm sớ
Lời giải
Đồ thị hàm số
hồnh nên

có hai điểm cực trị nằm về hai phía so với trục
có 3 nghiệm đơn.

Vậy số điểm cực trị của hàm số
Bài 9: Cho hàm số

là 3 + 2 =5.
với

. Hàm số

có bao nhiêu điểm cực trị?

Lời giải

Theo giả thiết ta có


để
9


Điều đó chứng tỏ rằng, phương trình

có 4 nghiệm phân biệt. Do đó, hàm số

phải có 3 điểm cực trị. Vì vậy, hàm số

có 4 + 3 = 7 điểm cực trị

Bài 10: Tính tổng các giá trị của tham số m để hàm số
5 điểm cực trị.
Lời giải
Vẽ đồ thị hàm số

có 2 điểm cực trị nên
Û

cũng có 2 điểm cực trị.

số giao điểm của đồ thị

Để số giao điểm của đồ thị
thị

m
2 có


f  x   x3  3x 2  9 x  5

Ta thấy hàm số
Yêu cầu bài toán

y  x3  3 x 2  9 x  5 

với trục hoành là 3.

với trục hoành là 3 ta cần tịnh tiến đồ

theo phương Oy lên trên một đoạn có độ dài nhỏ hơn 32 đơn vị
Vì

nên

. Vậy tổng các giá trị của

tham số m là 2016.
Bài 11: (HSG Vĩnh Phúc 2018-2019). Tìm tất cả các giá trị thực của tham số
để hàm số

có đúng năm điểm cực trị.

Lời giải Xét hàm số
Bảng biến thiên hàm số
x
y’
y


0

2

0

0

m-2
m-6

Hàm số đã cho có đúng 5 điểm cực trị
nghiệm phân biệt

phương trình f(x) = 0 có đúng 3

.
Vậy với
thì hàm số đã cho có đúng 5 điểm cực trị.
Bài 12: (Câu 43 đề minh họa 2018 của Bộ GD&ĐT).

10


Có bao nhiêu giá trị nguyên của tham số
có 7 điểm cực trị?
Lời giải

Xét hàm số


để hàm số

có

Lập BBT của đồ thị hàm số
x
-1
y’
0
y
m-5
Để đồ thị hàm số
0 có đúng 4 nghiệm phân biệt:

+

0
0
m

ta có
2
0

+

m-32
có 7 điểm cực trị

phương trình f(x) =


Vì
Vậy có 4 giá trị ngun của m thỏa mãn u cầu bài tốn.

Bài 13: Cho hàm số
có đồ thị như hình vẽ
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
có

đúng 3 điểm cực trị.

Lời giải
Xét

11


Tính được
Bảng biến thiên của hàm số g(x)
x
g’
g

-

a
0

+


1
0
g(1)

3
0

g(a)

+

m

Dựa vào bảng biến thiên, suy ra đồ thị hàm số g ( x ) có

3

điểm cực trị.

Suy ra đồ thị hàm số

có 3 điểm cực trị

khi và chỉ khi

Cách 2:

Xét

Bảng biến thiên của hàm số g(x)

x
g’
g

-

a
0
g(a)

+

1
0
g(1)

3
0

+

m
12


Dựa vào bảng biến thiên, suy ra đồ thị hàm số g ( x ) có

3

điểm cực trị.


Suy ra đồ thị hàm số
có 3 điểm cực trị
khi và chỉ khi đồ thị hàm số g(x) nằm hồn tồn phía trên trục Ox (kể cả tiếp
xúc)
1.2.Bài toán mở rộng 1: “Cho hàm số
số

. Hỏi số điểm cực trị của hàm

”

Bài 1: Cho hàm số

có đồ thị như hình vẽ. Hàm số

có bao nhiêu điểm cực trị?
Lời giải
Cách 1: Từ đồ thị hàm số
Từ đồ thị hàm số

suy ra đồ thị hàm số

suy ra đồ thị hàm số

Nhìn đồ thị hàm số

ta thấy,hàm số

Cách 2: Nhìn đồ thị hàm số

+ Đồ thị hàm số

có 7 điểm cực trị?

ta thấy

có 3 điểm cực trị.

+ Phương trình

có 4 nghiệm đơn.

+ Phương trình

có 0 nghiệm bội lẻ.

Suy ra, hàm số

có 3 + 4 = 7 điểm cực trị.

+ Vì số điểm cực trị của hàm số
nên hàm số

bằng số điểm cực trị của hàm số

Bài 2: Cho hàm số

có 7 điểm cực trị.
có đạo hàm


. Hàm sớ

có nhiều nhất bao nhiêu điểm cực trị?
Lời giải

+
Suy ra hàm số

;
có 3 điểm cực trị.
13


+ Số giao điểm của đồ thị

và trục hoành nhiều nhất là 4 hay phương

trình
có nhiều nhất 4 nghiệm.
Vậy hàm sớ
có nhiều nhất 3 + 4 = 7 điểm cực trị.
Vậy hàm sớ

có nhiều nhất 3 + 4 = 7 điểm cực trị.

Bài 3 : Cho hàm số
có đồ thị như hình vẽ
Có bao nhiêu giá trị ngun của tham số
để hàm số
có


điểm cực trị ?

Lời giải
Từ đồ thị hàm số ta thấy: Hàm số
Hàm sớ

có điểm cực trị dương.

có 2.2 + 1 = điểm cực trị.

Hàm sớ

có điểm cực trị với mọi m.

Vậy có vơ số giá trị m để hàm số

có

1.3. Bài toán mở rợng 2: “Cho hàm số

. Hỏi số điểm cực trị của hàm

số

điểm cực trị.

”

Bài 1: Cho đồ thị của hàm số


như hình vẽ.

Tìm sớ điểm cực trị của đồ thị hàm số
Lời giải
Cách 1: Từ đồ thị của hàm số

:
suy ra đồ thị

hàm số
Từ

đồ thị của hàm số

Dựa vào đồ thị hàm số
cực trị

suy ra đồ thị hàm số

suy ra có 5 điểm

Cách 2:
+ Hàm số y = f(x) + 2 có 3 điểm cực trị.
+ Phương trình f(x) + 2 = 0 có 2 nghiệm đơn.
+ Phương trình f(x) + 2 = 0 có 0 nghiệm bội lẻ.
Vậy số điểm cực trị của hàm số

bằng 3 + 2 + 0 = 5.
14



2: Cho hàm sớ
có đồ thị như hình bên
Bài
dưới. Tính tổng các tung độ của các điểm cực trị của đờ
thị hàm số
Lời giải
Đồ thị hàm số

có được bằng cách

- Tịnh tiến đồ thị hàm số

theo phương Oy lên 4 đơn vị ta được
qua trục Ox ta

- Lấy đối xứng phần phía dưới trục Ox của đồ thị hàm số
được

Dựa vào đồ thị hàm số
suy ra tọa độ các điểm cực trị là (-1 ;0),
(0 ;4), (2 ;0). Vậy tổng tung độ các điểm cực trị bằng 0 + 4 + 0 = 4
Bài 3: Cho hàm số

xác định, liên tục trên  và có bảng biến thiên như

hình vẽ. Hỏi đồ thị hàm số

có bao nhiêu điểm cực trị ?

x
y’
y

+

-1
0
2018

-

+

-2018

Lời giải

có được từ đồ thị f ( x ) bằng cách tịnh tiến

Đồ thị hàm số
đồ thị

3
0

sang phải 2017 đơn vị và lên trên 2018 đơn vị.

Suy ra bảng biến thiên của
x

u’
u

+

2016
0
4036

-

2020
0
0

+
15


+ Hàm số y = u(x) có 2 điểm cực trị.
+ Phương trình
+ Phương trình

có 1 nghiệm đơn.
có 0 nghiệm bội lẻ.

Vậy số điểm cực trị của hàm số

bằng 2 + 1 + 0 = 3.


Cho hàm số
xác định trên
và liên tục trên từng khoảng
Bài 4:
xác định, có bảng biến thiên như hình vẽ. Tính tổng tung độ các điểm cực trị của
đồ thị hàm số
x
y’
y

-

-1
||
||

3
0

-

+

-1
Lời giải
Bảng biến thiên của hàm sớ

như hình vẽ
x
g’

g

-

-1
||
||

3
0

-

+

-4
+ Đờ thị hàm sớ

có 1 điểm cực trị A(3;-4) nên đồ thị hàm số

có 1 điểm cực trị là A’(3;4)
Phương trình
có 3 nghiệm đơn nên đồ thị hàm số
điểm cực trị đều có tung độ là 0.
Vậy số điểm cực trị của hàm số

có 3

bằng 1+ 3 + 0 = 4


Suy ra tung độ các điểm cực trị là 4 + 0 + 0 + 0 = 4
Bài 5: Cho hàm số
. Hàm số

thỏa mãn

và có đạo hàm
có bao nhiêu điểm cực trị?

Lời giải

16


+
+ Bảng biến thiên

;

.

x
y’
y

+

-2
0
0


-

0
0

+

2
0
0

-

y(0)
+ Hàm số

có 3 điểm cực trị.

+ Phương trình
+ Phương trình

có 0 nghiệm đơn.
có 0 nghiệm bội lẻ.

Vậy hàm số

có 3 + 0 + 0 = 3 điểm cực trị.

Bài 6: Cho hàm số


biết

số điểm cực trị của đồ thị hàm số
Lời giải

và

. Tìm

.

Cách 1: Đặt

+ Từ giả thiết

đồ thị hàm số h(x) có 3 điểm cực trị.

+ Ta có

phương trình

thuộc khoảng

có nghiệm

có 4 nghiệm phân biệt (dáng điệu của hàm trùng

phương). Vậy hàm số


có 7 điểm cực trị.

Cách 2: Với bài tập trắc nghiệm ta có thể tìm đáp số theo cách sau:

Chọn
Vẽ phác họa đồ thị hàm sớ

, ta thấy đờ thị hàm số

có 7 điểm cực trị.
Bài 7: Cho hàm số

với m là tham số

thực. Tìm số điểm cực trị của đồ thị hàm số
Lời giải
17


Cách 1: Ta có:

Suy ra
+

;
có 3 nghiệm đơn phân biệt vì

hàm sớ

với mọi m (hay


có 3 điểm cực trị)

+
.
vơ nghiệm. Vậy hàm số
có 3 cực trị.
Cách 2: (Trong bài trắc nghiệm để tìm nhanh kết quả ta nên đặc biệt hóa
bài toán)
. Ta đi tìm số điểm cực

Ta cho m = 0, ta được hàm số
trị của hàm số

x  0

 x  2
f  x   1  x 4  4 x 2  16  g   x   4 x 3  8 x g   x   0  4 x3  8 x  0  x   2

Đặt
Bảng biến thiên

;

x
g’
g

-


0

+

0
0
16

12
Do đồ thị hàm số
số

-

0

.

+

12

nằm hoàn toàn bên trên trục hồnh nên đồ thị hàm

cũng chính là đồ thị của hàm số

. Khi đó số điểm cực

là 3 .


trị của hàm số

  có đồ thị như hình vẽ. Tìm tất
Bài 8: Cho hàm số
cả các giá trị thực của tham số m để hàm số
y f x

có 5 điểm cực trị
Lời giải
Vì hàm
trị.

đã cho có 2 điểm cực trị nên

cũng có 2 điểm cực

18


Để hàm số

có 5 điểm cực trị

số giao điểm của đờ thị

với trục hồnh là 3.
Để số giao điểm của đồ thị

với trục hoành là 3, có 2 trường hợp xảy ra


Tịnh tiến đồ thị
hơn 1 đơn vị

theo phương Oy xuống phía dưới một đoạn có độ dài nhỏ

Tịnh tiến đồ thị
đơn vị

theo phương Oy lên trên một đoạn có độ dài nhỏ hơn 3

Vậy
Bài 9: Cho hàm số

thoả mãn
. Tìm số điểm cực trị của hàm số

Lời giải

Xét
, ta có
Do đó đồ thị hàm số
cắt trục hồnh tại ba điểm phân biệt và suy ra hàm
số

có hai điểm cực trị

Vậy số điểm cực trị của đồ thị hàm số

là 2 + 3 = 5


BÀI TẬP TỰ LUYỆN DẠNG 1
Câu 1: Đồ thị hàm số
A. 3

B. 0

có bao nhiêu điểm cực trị?
C. 1
D. 2

Câu 2: Số điểm cực trị của hàm số
A. 2
B. 1
Câu 3: Cho hàm số
xác định trên
xác định, có bảng biến thiên như hình vẽ.

là:
C. 4

D. 3
và liên tục trên từng khoảng

19


Đồ thị hàm số

có bao nhiêu điểm cực trị?


A. 4

B. 3

C. 1

Câu 4: Cho đồ thị của hàm số

như hình vẽ.

Số cực trị của đồ thị hàm số
A. 5

D. 2

là:

B. 2

C. 3

D. 4

Câu 5: Cho đồ thị của hàm số

như hình vẽ.

Số cực trị của đồ thị hàm số

là:


A. 5

B. 6

C. 7

Câu6: Cho hàm số bậc ba
và
A. 1

với

, biết

,

. Tìm số điểm cực trị của đồ thị hàm số

B. 5

C. 3

Câu 7: Cho hàm số
trị của hàm số
A. 1

D. 4

với

là:
B. 5

D. 7

,

và
C. 3

. Số cực
D. 7

Câu 8: Cho hàm số
m là tham số. Tìm số cực trị của hàm số
A. 2
B. 5
Câu 9: Có bao nhiêu số nguyên
đúng 5 điểm cực trị
A. 12
B. 15

, với
C. 4

D. 7

để hàm số
C.16


có
D. 17

DẠNG 2: CÁC BÀI TOÁN CỰC TRỊ CỦA HÀM SỐ
20


Để giải quyết các bài toán cực trị của hàm số
cách sau:

ta dùng một trong ba

Cách 1: Lập bảng biến thiên của hàm số
Cách 2: Sử dụng phép biến đổi đồ thị: Từ đồ thị

suy ra đồ thị

Cách 3: Để giải quyết các bài toán trên ta vận dụng nhận xét sau:
Nhận xét: Gọi k là số điểm cực trị dương của hàm số
thì số điểm cực
trị của hàm số
Thật vậy

bằng 2k + 1

+ Theo giả thiết k là số điểm cực trị dương của hàm số
nghiệm dương
+ Vì đồ thị
và
đồ thị đối xứng nhau qua Oy

nghiệm âm
+ Vì đồ thị hàm số
và đồ thị hàm số
Oy nên f’(x) đổi dấu khi qua điểm x = 0
Vậy số điểm cực trị của hàm số

có k
có k

đối xứng nhau qua trục

bằng 2k + 1

2.1 Bài toán cơ bản. “Cho đồ thị của hàm số

. Hỏi số điểm cực trị của

hàm số
Bài 1: Cho hàm số
Hàm số

có đồ thị như hình vẽ bên.

có bao nhiêu điểm cực trị?

Lời giải
Cách 1: + Từ đồ thị hàm số

ta suy ra đồ thị hàm


số
Dựa vào đồ thị hàm số
Cách 2: + Hàm số
+ Vậy hàm số

có 7 cực trị.
có 3 điểm cực trị dương
có 3.2 + 1 = 7 điểm cực trị
21


Bài

2: Cho hàm số

xác định và liên tục trên

, có bảng biến thiên như

hình vẽ. Tìm số điểm cực trị của hàm số
x

1

-2

y’

+


y

0

-

4

0

+

f(-2)

0

-

f(4)
f(1)

Lời giải
Hàm số có hai điểm cực trị dương, suy ra số điểm cực trị của hàm số
là 2.2 + 1 = 5
Bài 3: Cho hàm số y = f(x) có đạo hàm

với

Tìm số điểm cực trị của hàm số


Lời giải Ta có
Vì
cực trị.

có 2 nghiệm bội lẻ (x = -3 và x = 2) nên hàm số y = f(x) có 2 điểm

Hàm số y = f(x) có 1 điểm cực trị dương nên
cực trị.
Bài 4: Có bao nhiêu số nguyên

có 2.1 + 1 = 3 điểm

để hàm sớ

có đúng 5 điểm cực trị.
Lời giải
Hàm sớ

có đúng 5 điểm cực trị.
có hai điểm cực trị dương

có hai nghiệm

dương.
có hai nghiệm dương.
(vì

)

2.2 Bài toán mở rợng 1. “Cho đồ thị của hàm số


. Hỏi số điểm cực trị

của hàm số
22


Bài 1: Cho hàm số

có đồ thị như hình vẽ bên.

Hàm số
có bao nhiêu điểm cực trị?
Lời giải
Cách 1: + Từ đồ thị của hàm số
suy ra đồ thị hàm số
.
Nhìn đồ thị ta thấy,hàm số

có 7 điểm cực trị.

Cách 2:

Bảng xét dấu g’(x)
x
-a+1
-1
0
1
y’

0
+
- 0 + || Vậy đồ thị hàm số đã cho có 7 điểm cực trị .

2
0

Bài 4: Cho hàm số đa thức bậc bốn

có 3 điểm cực trị

Có bao nhiêu số nguyên
Lời giải
Hàm số

để hàm số

có 7 cực trị

Các điểm cực trị của hàm số

+

3
0

a+1
-

+

.

có 7 điểm cực trị.
có 3 điểm cực trị lớn hơn -m

là

Vậy ta có điều kiện là
2.3 Bài toán mở rợng 2. “Cho đồ thị của hàm số

. Hỏi số điểm cực trị

của hàm số

23


Bài 1: Cho hàm số

có đồ thị như hình bên dưới.

Đồ thị hàm số
Lời giải
Cách 1:

có bao nhiêu điểm cực trị ?

+ Từ đồ thị hàm số

suy ra đồ thị hàm số


+ Từ đồ thị hàm số

suy ra đồ thị hàm số

Nhìn đồ thị hàm số

ta thấy: Đồ thị hàm số

có 5 điểm cực trị.
Cách 2: Dựa vào nhận xét 2: Từ đồ thị ta thấy hàm số
dương nên hàm số

có 2 điểm cực trị

có 5 điểm cực trị.

Suy ra hàm số
thay đổi cực trị).
Bài 2: Cho hàm số

có 5 điểm cực trị (vì phép tịnh tiến khơng làm
có đồ thị như hình vẽ. Đồ thị hàm

số
Lời giải

có bao nhiêu điểm cực trị ?

Từ đồ thị


suy ra đồ thị

bằng cách:

+ Giữ nguyên phần đồ thị hàm số
ở bên
phải trục tung (kể cả những điểm nằm trên trục tung).
+ Bỏ phần đồ thị hàm số

ở bên trái trục tung.

+ Lấy đối xứng phần đồ thị hàm số
trục tung.
Từ đồ thị

suy ra đồ thị

Tịnh tiến đồ thị hàm số

ở bên phải trục tung qua
bằng cách:

theo phương trục Ox sang phải 2 đơn vị.

24


Dựa vào đồ thị, suy ra hàm số
Bài 3: Cho hàm số


có đồ thị như hình vẽ. Đồ thị

hàm số
Lời giải
Cách 1:

có 5 điểm cực trị.

có bao nhiêu điểm cực trị ?

Xét hàm số

Ta có

Ta có g’(x) khơng xác định tại

Bảng biến thiên

x
g’
g

-

1
0

2
||

-2

+

3
0

-

-3
Dựa vào BBT của hàm số
Bài 4 : Cho hàm số

+

-3
ta thấy hàm số có 3 điểm cực trị.

liên tục trên
x
f’
f

.

+

và có bảng xét dấu như hình vẽ:
0
0

f(0)

-

2
0

+

f(2)
Hàm số

có bao nhiêu điểm cực trị?

Lời giải

25