ĐỀ MẪU CĨ ĐÁP ÁN

ƠN TẬP KIẾN THỨC
TỐN 12
Thời gian làm bài: 40 phút (Không kể thời gian giao đề)
-------------------------

Họ tên thí sinh: .................................................................
Số báo danh: ......................................................................
Mã Đề: 031.
Câu 1. Cho hai số phức

Phần thực của số phức

A. .
Đáp án đúng: C

B.

.

C.

là.

.

D.

.

Giải thích chi tiết: Ta có
Do đó phần thực của số phức
Câu 2. Tập xác định
Ⓐ.

là

của hàm số

. Ⓑ.

. Ⓒ.

A.
Đáp án đúng: A

là
. Ⓓ.

B.

Câu 3. Tìm tập nghiệm
A.

.

.
C.

của bất phương trình


.

.

B.

C.
.
Đáp án đúng: D

D.

Giải thích chi tiết: [Mức độ 3] Tìm tập nghiệm
A.

.

B.

C.
Lời giải
Điều kiện:

.

D.

.


của bất phương trình

.

.

.
D.

.

.

1


.
Kết hợp với điều kiện

. Khi đó tập nghiệm của bất phương trình là

Câu 4. Cho hình hộp

có đáy ABCD là hình thoi tâm

và cạnh bên hợp với đáy một góc bằng
A.
Đáp án đúng: C

B.


B.

Câu 6. Cho hình chóp

A.
.
Đáp án đúng: B

của khối đa diện

Tính
C.

có đáy

D.

là hình vng cạnh bằng

. Hình chiếu vng góc của

là điểm
thuộc đoạn
thoả mãn
và
(mặt cầu tiếp xúc với tất cả các mặt bên của hình chóp)
B.

.


. Biết

D.

thỏa mãn

A.
Đáp án đúng: C

, cạnh a, góc

C.

Câu 5. Cho số phức

mặt phẳng
tiếp hình chóp

. Tính thể tích

.

C.

.

trên

. Tính bán kính mặt cầu nội


D.

.

Giải thích chi tiết:
Gọi

là tâm mặt cầu nội tiếp hình chóp

và là bán kính mặt cầu nội tiếp hình chóp

.
2


Ta có
Mặt khác, ta lại có:

Suy ra

.

Ta tính được thể tích khối tứ diện đều là

.

Từ

ta dựng đường thẳng song song với


cắt

lần lượt tại

Từ

ta dựng đường thẳng song song với

cắt

lần lượt tại

Ta có

và

Suy ra

và

Do đó

và
và

.

và


Do đó, từ (*) ta suy ra:

.

Câu 7. Tập nghiệm của bất phương trình
A.
.
Đáp án đúng: D

B.

là
.

C.

.

D.

.

Giải thích chi tiết:

.
Câu 8. Tổng hai nghiệm của phương trình
A.
Đáp án đúng: D
Giải thích chi tiết:


B.

bằng:
C.

D.

+) Có PT
3


+) Đặt
+) PT trở thành

.

Câu 9. Cho hình chóp

có đáy

cho

thay đổi đi qua

. Mặt phẳng

là hình bình hành tâm
và

cắt các cạnh


lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của tỉ số
A. .
Đáp án đúng: C

B.

.

C.

thuộc đoạn

thay đổi đi qua

tại
A. . B.
Lời giải

. Gọi
. C.

lần lượt tại

.

có đáy

. Mặt phẳng


D.
là hình bình hành tâm
và

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của tỉ số
. D.

là điểm thuộc đoạn

sao
. Gọi

. Tính

Giải thích chi tiết: (VDC)Cho hình chóp
sao cho

. Gọi

cắt các cạnh

.
. Gọi

là điểm
lần lượt

. Tính

.


⬩ Ta có:
⬩ Đặt
⬩
⬩ Lại có
4


⬩ Khi đó
⬩ Xét hàm số

với

⬩ Ta có

⬩ Suy ra
Câu 10.

. Vậy

.

Cho hình phẳng giới hạn bởi các đường
khối trịn xoay có thể tích bằng

. Tìm

A.
C.
Đáp án đúng: B

Câu 11.
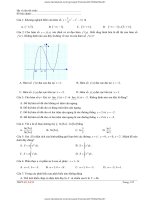
Cho hàm số

.

có đồ thị của hàm số

quay xung quanh trục

tạo thành

và
B.

.

D.

.

như hình vẽ

5


Hàm số
A.
.
Đáp án đúng: A


có mấy điểm cực trị ?
B.
.

Câu 12. Có bao nhiêu số phức z thỏa mãn
A. 3.
B. 1.
Đáp án đúng: A

C.

.

D.

và
C. 2.

.

.
D. 4.

Câu 13. Tìm nghiệm thực của phương trình
A.

B.

C.
Đáp án đúng: B


D.

Câu 14. Tính thể tích của khối lập phương có độ dài đường chéo bằng
A.

.

C.
.
Đáp án đúng: D
Câu 15.

B.

.

D.

.

Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh
góc giữa SA và mặt phẳng
A.

.

C.
Đáp án đúng: B


bằng

.

, cạnh bên SA vng góc với mặt phẳng đáy,

. Thể tích khối chóp S.ABCD bằng
B.
D.

.

6


Câu 16. Biết số phức thỏa điều kiện
phẳng. Diện tích của hình phẳng đó bằng:
A.
.
Đáp án đúng: D

B.

. Tập hợp các điểm biểu diễn của

.

C.

.


D.

tạo thành

hình

.

Giải thích chi tiết:
.
Gọi

.

Vậy tập hợp các điểm biểu diễn số phức
bán kính

và

Câu 17. Tính tổng

.
trên mặt phẳng phức là hình vành khăn giới hạn bởi hai đường trịn

Diện tích

.

tất cả các nghiệm của phương trình


A.
.
Đáp án đúng: B

B.

.

C.

.

D.

.

Giải thích chi tiết: Ta có:

Khi đó phương trình có dạng

với
đồng

Do

phương trình

nhiều nhất là hai nghiệm. Ta thấy


biến

trên

nên

từ

phương

có nhiều nhất là một nghiệm, từ đó phương trình
là hai nghiệm của phương trình

trình

có

.

Vậy phương trình có hai nghiệm là

7


Câu 18. Cho hình chóp
tích

có đáy

của khối chóp


là hình vng cạnh

biết

A.
.
Đáp án đúng: A

.

Giải thích chi tiết: Cho hình chóp

A.
B.

C.
có đáy

của khối chóp

.

D.

là hình vng cạnh

biết

.

,

,

.

.
.
.

Câu 19. Cho hình chóp
cầu ngoại tiếp hình chóp
A.
.
Đáp án đúng: B

có đáy là tam giác vng,
bằng
B.

Giải thích chi tiết: Cho hình chóp
của mặt cầu ngoại tiếp hình chóp
A.
Lời giải

. Tính thể

.

C.

D.

,

.

B.

. Tính thể tích

,

. B.

.

C.

.

C.
có đáy là tam giác vng,
bằng
. D.

Diện tích của mặt

.

D.


.
Diện tích

.

8


Gọi

là trung điểm của
vng có

Khi đó
Mặt khác,
Suy ra
Từ (1), (2) suy ra

cân tại

nên

vng cân tại

và

(1).

có


nên tam giác

vng cân tại

(2).
là tâm mặt cầu ngoại tiếp hình chóp

Suy ra
Vậy diện tích mặt cầu ngoại tiếp hình chóp
Câu 20.
Cho hàm số

liên tục trên

là

và có bảng biến thiên như hình dưới đây. Gọi

giá trị lớn nhất và giá trị nhỏ nhất của hàm số

A. .
Đáp án đúng: A
Câu 21.

B.

(đvdt).

.


trên

C.

. Giá trị của

.

và

lần lượt là

bằng bao nhiêu?

D. .

9


Trong mặt phẳng phức
tơ đậm trong hình vẽ ?

, số phức

A.
C.
Đáp án đúng: C

,


và

.

B.

và

.

và

.

D.

và

.

Giải thích chi tiết: Từ hình vẽ ta có

và

Câu 22. Cho hình lăng trụ đều
bằng
A.
.
Đáp án đúng: A

Câu 23.

và vng góc với

A.

Đường thẳng

bằng
D.
và

B.

B.

đi qua

. Đường thẳng

đi

.

D.

VTPT của mặt phẳng

.


có phương trình là

và vng góc với

.

D.

, cho mặt phẳng

Giải thích chi tiết: Trong khơng gian

A.
Lời giải

.

C.

.

đi qua

. Thể tích khối lăng trụ

. Khi đó tích phân

C.
.
Đáp án đúng: C


thẳng

,

C.

B.

Câu 24. Trong không gian
qua

.

và

A.
Đáp án đúng: A

.

biết

B.

Cho

thỏa điều kiện nào thì có điểm biểu diễn thuộc phần

, cho mặt phẳng


và

. Đường

có phương trình là

.
là

.

C.

.

D.

.

.
và có VTCP là

hay
10


Phương trình đường thẳng
Câu


25.

Gọi

là

là

diện
. Gọi

.
tích
,

hình

phẳng

giới

hạn

bởi

:

và

lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của


khi

. Tính

?
A.
.
Đáp án đúng: B

B.

.

C.

.

Giải thích chi tiết: Xét phương trình hồnh độ giao điểm của

D.
và

.

:

·

Do


nên

và

Diện tích hình phẳng giới hạn bởi

và

là:

.
Vì hàm số:

đồng biến trên đoạn

nên

,

.

Vậy
Câu 26. Cho phương trình
đây?
A.
C.
Đáp án đúng: C

. Đặt


.

Phương trình

B.
.

.

D.

Câu 27. Trong hệ trục tọa độ

, có bao nhiêu điểm

.

trên trục hồnh có hồnh độ ngun sao cho từ

kẻ được hai tiếp tuyến đến mặt cầu
A. .
Đáp án đúng: D

B.

trở thành phương trình nào dưới

và song song với
.


C.

.

.

D.
11


Giải thích chi tiết: Trong hệ trục tọa độ
cho từ

, có bao nhiêu điểm

trên trục hồnh có hồnh độ ngun sao

kẻ được hai tiếp tuyến đến mặt cầu

và song song với

.
A. . B.
Lời giải

. C.

Gọi


. D.

. Gọi

là mặt phẳng chứa hai tiếp tuyến.

Khi đó

Ta có:
Loại

vì

. Vậy có

Câu 28. Cho hai hàm số

và

Tính tích phân
B.

A.
Đáp án đúng: A
Giải thích chi tiết:
Lời giải.

điểm

thỏa đề.


có đạo hàm liên tục trên

thỏa mãn

C.

và

D.

Từ giả thiết

Do đó từ

, suy ra

Tích phân từng phần ta được

Câu 29. Cho số phức thỏa mãn
Tập hợp điểm biểu diễn số phức
phẳng phức là một đường thẳng. Phương trình đường thẳng đó là
A.
C.
Đáp án đúng: B

.

B.


.

.

D.

.

trên mặt

Giải thích chi tiết: Ta có:
Gọi
12


Ta có:
Kết luận: Tập hợp điểm biểu diễn số phức

trên mặt phẳng phức là một đường thẳng có phương trình

Câu 30.
Cho khối nón có chiều cao
A.

và đường kính đường trịn đáy là

.

B.


C.
.
Đáp án đúng: B

D.

Câu 31. Biết

với

A. .
Đáp án đúng: A

B.

Giải thích chi tiết: Đặt
Ta có

,

. Thể tích của khối nón đã cho bằng
.
.

là các số nguyên. Giá trị

.

C.


bằng

.

D.

.

và

và

Do đó
Suy ra
.
Câu 32. Trong khơng gian chỉ có
Tứ diện đều

loại khối đa diện đều.

Lập phương

Bát diện đều

12 mặt đều

20 mặt đều

Mệnh đề nào dưới đây là đúng?
A. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.

B. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
C. Mọi khối đa diện đều có số mặt là những số chia hết cho .
D. Khối lập phương và khối bát diện đều có cùng số cạnh.
Đáp án đúng: D
Câu 33. Cho

. Khi đó

A. .
Đáp án đúng: D

B.

.

bằng
C.

.

D.

.

13


Giải thích chi tiết: Cho
A. . B.
Lời giải


. C.

. D.

. Khi đó

.

Ta có:
Câu 34. Cho hình trụ có bán kính đáy
cho bằng
A.
B.
Đáp án đúng: C
Câu 35. Cho số phức
A.
.
Đáp án đúng: B

.

B.

.
và độ dài đường sinh

D.

. Tìm tọa độ của điểm


B.

.

C.

thỏa mãn

. C.

Ta có
Vậy điểm biểu diễn

Diện tích xung quanh của hình trụ đã

C.

thỏa mãn

Giải thích chi tiết: Cho số phức
A.
Lời giải

bằng

của số phức

là


biểu diễn số phức

.
. Tìm tọa độ của điểm

. D.

.

. Suy ra

.

D.

.
.

biểu diễn số phức

.

.
----HẾT---

14