Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

CHƯƠNG 2
CÁC NGUYÊN LÝ BIẾN ĐỔI
NĂNG LƯỢNG ĐIỆN CƠ
Trong chương này chúng ta xem xét tới các quá trình biến đổi năng lượng điện
cơ xảy ra trong các môi trường điện trường và từ trường trong các thiết bị biến đổi năng
lượng. Mặc dù rằng có rất nhiều thiết bị biến đổi hoạt động dựa trên cùng một nguyên
lý, nhưng cấu trúc của chúng lại phụ thuộc vào chức năng công tác. Các thiết bị đo lường
và kiểm tra thông thường là các thiết bị trung gian, chúng vận hành dưới các điều kiện
đầu vào, đầu ra tuyến tính và với các tín hiệu tương đối nhỏ. Có thể đưa ra một số ví dụ
về loại này như các máy microphone, loa phóng thanh.... Dạng thiết bị thứ hai bao gồm
các thiết bị sinh lực tác động như cuộn dây solenoide, relay, các nam châm điện... Dạng
thứ ba bao gồm các thiết bị biến đổi năng lượng thường xuyên như các động cơ điện,
máy phát điện. Ngoài ra, trong chương trình cịn đề cập tới các ngun lý biến đổi năng
lượng điện cơ và phân tích các hệ thống sử dụng từ trường như là mơi trường biến đổi.
Mục đích của các phân tích được nhắm vào ba điểm chính:
1- Giúp ta hiểu sự biến đổi năng lượng xảy ra như thế nào.
2- Cung cấp các phương pháp để thiết kế và tối ưu hóa các thiết bị theo yêu cầu
đặc biệt.
3- Cho thấy cách thực hiện các mơ hình thiết bị biến đổi năng lượng điện-cơ có
thể áp dụng trong việc phân tích các thành phần của một hệ thống kỹ thuật.
Trong chương này ta xem xét các thiết bị trung gian và các thiết bị sinh lực tác
động, còn các thiết bị biến đổi năng lượng thường xuyên được trình bày trong các
chương khác.
Các khái niệm và phương pháp trình bày ở đây là hồn tồn có sức mạnh, chúng
có thể được áp dụng trong một dãy rộng các tình huống kỹ thuật, gắn liền với sự biến
đổi năng lượng điện cơ.
2.1 LỰC VÀ NGẪU LỰC TRONG CÁC HỆ THỐNG TRƯỜNG ĐIỆN TỪ.
1. Định luật về lực lorentz
F= q(E + vB)

(2.1)
Cho lực F tác động lên điểm có điện tích q nằm trong điện trường và từ trường.
Trong hệ đo lường quốc tế SI: F - được tính bằng Newtons; q - Coulombs; E Volt/metre; B - Teslas và v - tốc độ tương đối của điểm xét so với từ trưòng m/s.
Như vậy trong một hệ thống điện trường đơn thuần, lực được xác định đơn giản
bởi điện tích của điểm và điện trường E.
F= qE
(2.2)
Lực tác động theo chiều của từ trường và độc lập so với sự chuyển động của điểm xét.
Trong các hệ thống từ trường, tình trạng trở nên phức tạp hơn. Ở đây lực có giá
trị:
F = q(v x B)
(2.3)
Nó được xác định bởi lượng điện tích của điểm, độ lớn của từ trường B và tốc độ chuyển
động của hạt. Trên thực tế chiều của lực ln vng góc với cả hai chiều chuyển động
của điểm và chiều của từ trường. Về mặt tốn học đó là tích vectơ v x B trong pt (2.2).
Độ lớn của tích này bằng tích của hai độ lớn v và B nhân với sin của góc giữa chúng.

46


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Chiều của lực F có thể tìm được
theo quy tắc bàn tay phải. Quy tắc này
phát biểu như sau: Khi ngón tay cái của
bàn tay phải chỉ chiều của v và ngón tay
chỏ chỉ chiều của B, lực có chiều đâm
xun từ lịng bàn tay ra phía ngồi
(H2.1).
Trong tình huống ở đó phần lớn

các điểm điện tích chuyển động, nên viết
lại biểu thức (2.3) theo mật độ dòng điện,
trong trường hợp đó lực sẽ là lực đơn vị:
F = J x B N/m3
(2.4)

Hình 2.1

2. Lực điện động, định luật BiotSavart-Laplace
Trong trường hợp chung nhất có thể xem lực điện động được sinh ra khi có sự
tác động tương hỗ giữa dòng điện và từ trường. Theo định luật Biot-Savart-Laplace, vi
phân lực điện động, tác động lên dòng điện i trên chiều dài của đoạn dl nằm trong từ
trường có từ cảm B được xác định bởi tích véctơ:
(2.5)
d F  idl  B
trong đó:Ġcó chiều theo chiều của dịng điện i.



Như đã biết, chiều của lực dF vng góc với cả hai vectơ d l và B , còn độ lớn
của nó là:
dF  idl.B sin 

trong đó:  là góc giữa dịng điện i và từ cảm B.
Nếu từ trường là khơng đổi so với dịng điện i trên tồn bộ chiều dài l của một
dây dẫn thẳng thì lực có giá trị bằng:
F = il.B sin
(2.6)
Khi  = /2: F = il.B
(2.7)

Chiều của lực điện động có thể được xác định theo quy tắc bàn tay trái. Quy tắc
này phát biểu như sau: Nếu từ trường B có chiều đâm xun qua lịng bàn tay trái, chiều
các ngón tay chỉ chiều dịng điện, thì chiều của lực điện động là chiều của ngón tay cái
chỗi ra.
Cơng thức Biot-Savart-Laplace dùng để xác định lực điện động khi ta có thể biểu
diễn từ cảm B bằng một biểu thức phân tích phụ thuộc vào kích thước của mạch vịng
dẫn điện. Để minh họa cho điều vừa nói ở trên, có thể đưa ra hai trường hợp tiêu biểu
sau đây:
1. Xác định lực điện động giữa hai dây dẫn song song có tiết diện nhỏ
Trong trường hợp các dây dẫn có tiết diện ngang nhỏ, thì đường dịng điện được
xem như trùng với đường trục của dây dẫn, vì vậy tiết diện của nó khơng có ảnh hưởng
gì tới lực điện động. Xét hai dây dẫn song song như được mô tả trong (H2.2), chúng có
chiều dài tương ứng là l1 và l2, được đặt cách nhau một khoảng cách bằng a.
Theo định luật Biot- Savart - Laplace, dòng điện i1 chạy trong vi phân dy của dây
dẫn 1 gây ra trên vi phân dx của dây dẫn 2 một vi phân từ cảm dB bằng:
dB  d o H 

 o i 1dy
.
sin 
4 r 2
47

(2.8)


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

trong đó:o- độ từ thẩm của khơng khí
bằng 4.10-7 (H/m)

- góc giữa dây dẫn l1 và
bán kính nối giữa dy và dx.
Như vậy, dịng điện i1 chạy trong
tồn bộ chiều dài l1 sẽ sinh ra từ cảm B
trong vi phân dx là:
l1

l

1

dy
B   dB  o .i 1  2 sin 
4 0 r
0

(2.9)
từ (H2.2) ta có thể đổi biến như sau:
y = a/tg; r = a/sin;
2
dy = -(a/sin )d
Sau khi thay vào biểu thức (2.9) nhận
được:
B

 o cos 1  cos  2
i1 .
4
a


(2.10)

Trong trường hợp đó, áp dụng cơng thức Biot- Savart - Laplace có thể xác định
vi phân lực tác động lên dx.
dFx 

o
.i 1 .i 2 .cos 1  cos  2 dx
4a

(2.11)

Tổng lực tác động lên dây dẫn l2 có dạng:
l2

Fx   dFx 
0

l

2
o
.i 1 .i 2  cos  1  cos  2 dx
4a
0

Giả thiết rằng l1 = l2 = l ta có thể viết:
cos  1 

lx


l  x 2  a 2

;

cos  2 

x
x2  a2

1 

0
1 x
x
dx
Từ đó: Fx 
i 1i 2  

2
2
2
2
4a

(
1

x
)


a
x

a
0 

2
 

a 
 2l
a
Fx  10  7 i 1 .i 2   1       (N)
Hay
l 
l
 a 


(2.12)
Từ cơng thức (2.12) có thể rút ra kết luận là: lực điện động
tác dụng lên hai dây dẫn đặt song song khi có các dịng điện i1, i2
khơng đổi chạy qua, chỉ phụ thuộc vào độ lớn của các dịng điện,
vào kích thước và vị trí tương đối giữa các dây dẫn với nhau.
Nếu gọi phần trong dấu móc của biểu thức là hệ số mạch
vịng Kv, thì:
Fx = 10-7 .i1.i2 Kv (2.13)
Trong trường hợp chiều dài của dây dẫn lớn rất nhiều so
với khoảng cách giữa chúng hay nếu a/l  0,1 thì KV = 2l/a, khi

đó:
48


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN
Fx  10  7 .i 1 .i 2

2l
(N) (2.14)
a

Trường hợp chiều dài của hai dây dẫn khác nhau như được biểu diễn trong (H2.3),
khi đó lực điện động cũng được tính theo cơng thức (2.13) với:
KV 

 CH   B
a

(2.15)

trong đó: CH - Tổng chiều dài các đường chéo.
B - Tổng chiều dài các cạnh bên.
2. Xác định lực điện động giữa hai dây dẫn song song có tiết diện lớn hình
chữ nhật
Hình 2.4: vẽ hai thanh dẫn
song song có tiết diện hình chữ
nhật, chúng có bề dày b rất nhỏ
so với chiều cao h và cách nhau
một khoảng a. giả thiết rằng
khoảng cách a nhỏ hơn rất nhiều

so với chiều dài của các thanh
dẫn và trên các thanh dẫn chảy
các dòng điện i1 và i2.
Nếu cho rằng dòng điện
phân bố đều trên tiết diện chữ
nhật của các thanh dẫn, thì trên
các vi phân dy và dx của chúng
sẽ chảy các vi phân dòng điện di1
và di2:
di 1  i 1

dy
dx
(2.16)
; di 2  i 2
h1
h2

Dọc theo chiều dài của các thanh dẫn, các vi phân dx và dy của chúng sẽ hình
thành các dây dẫn song song có tiết diện nhỏ và thỏa mãn điều kiện của cơng thức (2.14),
ta có thể viết:
dFr  10 7 i1 .i 2 .

2l dy dx
(2.17)
. .
r h1 h 2

Lực theo phương của bán kính r có thể phân tích thành hai thành phần:
Thành phần thứ nhất dFh tác động theo phương của chiều cao thanh dẫn h, đây

là hướng chịu lực tốt của các thanh dẫn chữ nhật vì vậy ta không quan tâm tới thành
phần lực này.
Thành phần thứ hai dFa tác động vng góc với các thanh dẫn. Nó có giá trị bằng:
dFa  dFr . cos   dFr .

a
r

(2.18)

Giả thiết rằng h1 = h2 = h, khi đó:
dFa  10 7 .i1 .i 2 .

dy.dx
2l
a. 2
2
y a
h
2

Tổng lực tác động theo hướng a sẽ nhận được sau khi lấy tích phân (2.19):

49

(2.19)


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN
h


Fa   dFa  10 7 .i 1 .i 2 .
0

 10 7 .i 1i 2

h

h

dy
2a.l
dx  2
2 
h 0 x a  y2

(2.20)


2al  h
h
h 2 

 (N)
2
arctg

ln
1




a
h2  a
a 2 


Nếu gom các đại lượng có liên quan tới kích thước trong biểu thức (2.20) thành các hệ
số Kv và Kq, thì
Fx  107 i1 .i2 .K v .K q
(2.21)
Kq - là hệ số ảnh hưởng của tiết diện dây dẫn lên lực điện động.
Từ các biểu thức (2.13) và (2.21) tính lực điện động có thể rút ra kết luận: lực
điện động có giá trị tỷ lệ với tích (bình phương) hai dịng điện với hệ số phụ thuộc
vào kích thước và hình dáng của mạch vịng dẫn điện.
Thơng thường trong tính tốn kỹ thuật, hệ số mạch vịng thường được tính sẵn
và đối với nhiều trường hợp phổ biến, chúng được đưa ra trong các sổ tay kỹ thuật điện.
Bảng 2.1 cho ta các công thức xác định lực điện động đối với một vài trường hợp thường
gặp trong thực tế tính tốn.

50


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

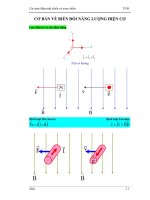
3. Lực điện động xoay chiều một pha
Do trên lưới điện xoay chiều dòng điện biến thiên theo thời gian, nên lực điện
động cũng biến thiên theo quy luật nhất định. Ta sẽ xem xét hai trường hợp tiêu biểu đối
với sự biến thiên của dòng điện trong lưới điện xoay chiều, đó là trường hợp dịng điện
biến thiên điều hịa và dịng điện xoay chiều có chứa thành phần khơng chu kỳ.

1. Khi dịng điện biến thiên điều hịa
Giả sử dịng điện biến thiên theo luật hình sin:
(2.22)
i  I m . sin t
ta có thể viết:
hay:

F

F  C.I 2m sin 2 t  CI 2m

1  cos 2t
(2.23)
2

Fm Fm

. cos 2t (2.24)
2
2

trong đó: C = 10-7KV - hằng số phụ
thuộc vào mạch vòng dẫn điện;
Fm = CI2m giá trị cực đại của
lực.
Như vậy, từ (2.24) thấy rằng,
lực xoay chiều bao gồm hai thành
phần:
Thành phần thứ nhất: không đổi
theo thời gian Fm/2.

Thành phần thứ hai: biến thiên
với tần số bằng hai lần tần số của dòng
điện (Fm/2) cos 2t.
Giá trị trung bình của lực xoay
chiều trong một chu kỳ bằng:
Ftb 

CI 2m Fm
1
Fdt


T
2
2

(2.25)

H2.5: cho ta thấy, lực điện động xoay chiều một pha có dạng đập mạch với tần
số gấp đơi tần số của dịng điện. Giá trị trunh bình của lực xoay chiều đúng bằng giá trị
của thành phần khơng đổi của nó.
2. Khi dịng điện xoay chiều có chứa thành phần khơng chu kỳ

51


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Hiện tượng nay thường
xảy ra trên lưới điện khi có

sự cố ngắn mạch, lúc nay
dịng điện sự cố ngồi
thành phần chu kỳ cịn
xuất hiện thành phần
khơng chu kỳ, mà giá trị
của nó tùy thuộc vào thời
điểm xảy ra ngắn mạch so
với thời điểm thành phần
xoay chiều đi qua trị số
zero. Trong tính tốn lực
điện động ta thường lấy
trường hợp nặng nề nhất là
khi ngắn mạch xảy ra ở
thời điểm cực đại của dịng
điện. Có thể mơ tả dịng điện theo biểu thức sau:



i  I m e  Rt / L  cos t



(2.26)

trong đó: R - điện trở của lưới điện bị ngắn mạch ();
L - tự cảm của nó (H); To = L/R- hằng số thời gian (s)
Tại thời điểm t = /, dòng điện đạt tới đỉnh cao nhất được gọi là dịng điện xung kích:
i XK  I m 1  e  ( pi / T .   K XK I m
(2.27)
Hệ số xung kích KXK phụ thuộc vào cơng suất của nguồn điện, vị trí của thiết bị

và hình dạng của lưới điện (đường dây trên không hay đường dây cable). Công suất
nguồn điện càng lớn, thiết bị càng gần nguồn thì hệ số này càng có giá trị lớn. Trong
tính tốn, thường chấp nhận KXK = 1,8.
Trong trường hợp dịng điện có chứa thành phần khơng chu kỳ, lực có thể được
biểu diễn.
2
F  CI 2m e  t / T  cos t 
(2.28)
Sự biến thiên theo thời gian của lực điện điện động được trình bày dưới dạng đồ thị
trong (H2.6). Giá trị lớn nhất của lực điện động xuất hiện ở bán kỳ đầu tiên kể từ thời
điểm xảy ra ngắn mạch.
Fm  CK 2XK .I 2m  C1,8 2 I 2m  C.3,24I 2m
(2.29)
Như vậy, khi dòng điện xoay chiều có chứa thành phần khơng chu kỳ thì lực điện
động sẽ lớn gấp 3,24 lần so với trường hợp dòng điện biến thiên điều hòa.
o

O

4. Lực điện động trên hệ thống điện ba pha
Trên hệ thống điện ba pha dòng điện pha này tương tác với dòng điện của hai pha
còn lại, chúng lệch pha nhau 120o. do các dòng điện lệch pha nhau, nên việc xác định
giá trị cực đại của lực điện động gặp khó khăn, nhất là trong trường hợp sự cố ngắn
mạch, khi trong thành phần của các dịng điện có chứa thành phần khơng chu kỳ.
1. Khi dịng điện các pha biến thiên điều hòa
Các dây dẫn trong hệ thống điện ba pha có thể được bố trí cách đều nhau trên
cùng một mặt phẳng hoặc trên các đỉnh của một tam giác đều.
Các dây dẫn bố trí song song trên cùng một mặt phẳng

52



Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Giả
thiết
rằng,
khoảng cách giữa các dây
dẫn nằm kề nhau (a) nhỏ
hơn rất nhiều so với chiều
dài của chúng (l). các dòng
điện chạy cùng hướng theo
hướng trục của dây dẫn.
Chiều dương của lực lấy
theo chiều của trục x (H2.7).
Giá trị tức thời của các dòng
điện pha sẽ là:



i1  I m sin t; i 2  I m sin(t  120o ); i 3  I m sin t  240o



Lực tác động lên các dây pha có dạng:
F1 = F12 + F13

(2.30)
(2.31)


Lực tác động lên các dây pha có dạng:
Ở đây: F12 - lực tác động giữa pha 1 và pha 2;
F13 - lực tác động giữa pha 1 và pha 3.
Áp dụng cơng thức (1.14) ta có thể viết:



2l 2
I m sin t. sin t  120o
a
2
 C1 I m sin t. sin t  120o

F12  10  7







(2.32)

-7

Trong biểu thức (2.32) C1 = 10 2l/a
F13 

C1 2
I m sin t. sint  240o 

2

(2.33)

Thay (2.32) và (2.33) vào (2.31) ta được:
1


F1  C1 I 2m sin t sint  120o   sint  240o 
2



(2.34)

Sau khi biến đổi lượng giác biểu thức (2.34) ta có dạng sau cùng là:



F1  0,866C1 I 2m sin t sin t  30o



(2.35)

Các cực trị sẽ ứng với t = 75 và t = -15 .
Thay thế t = 75o vào (2.35) sẽ nhận được giá trị cực đại của lực đẩy:
o

o


F1d max  0,805C1 I 2m

(2.36)

Thay thế t = -15 vào (2.35) sẽ có:
o

F1h max  0,055C1 I 2m

(2.37)
tương tự như cách làm đối với pha 1, lực tác động lên pha giữa sẽ có dạng:
(2.38)
F2  F21  F23  C1 I 2m sint  120o sin t  sint  240o 
Biến đổi lượng giác biểu thức (2.38) có thể đưa về dạng:
F2  0,866C1 I 2m cos2t  150o 
(2.39)
53


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Giá trị cực đại của lực tác động lên pha 2 sẽ ứng với t = 75o và lực đẩy lớn nhất
sẽ bằng lực hút lớn nhất.
(2.40)
F2d max  F2h max  0,866.C1 I 2m
Lực tác động lên pha 3 sẽ có dạng ngược với những gì xảy ra ở pha 1.
1

F3  C1 I 2m sint  240o  sin t  sint  120o 

2


(2.41)

khi đó, lực đẩy lớn nhất và lực hút lớn nhất:
F3d max  0,805C1 I 2m

(2.42)

và lực hút lớn nhất:
F3h max  0,055C1I 2m

(2.43)
Hình 2.7: mô tả sự biến thiên của lực theo thời gian ở các pha khác với trường
hợp lực điện động trên lưới điện xoay chiều một pha, các lực trên hệ thống điện ba pha
không những biến thiên theo thời gian, mà còn đổi dấu.
Lực tác động lên pha giữa (pha 2) là lớn nhất nên được dùng để tính tóan trong
kỹ thuật.
Ft max  0,866C1 I 2m  3.C1 I 2
(2.44)
Trong đó: I giá trị hiệu dụng của dịng điện.
Khi các dây dẫn bố trí trên đỉnh một tam giác đều
Với cách bố trí dây dẫn như vậy thì lực điện
động thay đổi cả về độ lớn và hướng tác động.
Cũng như trong trường hợp trước, ta có:
I1  I m sin t;

I 2  I m sint  120O ;
I 3  I m sint  240o .


Để dãù dàng biến đổi cơng thức khi tính lực
tác động lên dây dẫn ở pha 1, ta chọn trục tọa độ
với gốc nằm chính ở trên dây dẫn này như được
mô tả trong (H2.8). Lực điện động tác động vào
dây dẫn 1, sau khi chiếu lên trục x sẽ có giá trị:
F1x  F12 x  F13x

hay:

 







F1x  C1 I 2m sin t sin t  120o  sin t  240o cos 30o
2l
Trong đó C1  10 7
a

(2.46)

Sau khi biến đổi và rút gọn biểu thức (2.46) ta được



 23


F1x  C1 I 2m sin t sin t. cos120o  cos t sin120o   sin t cos 240o  cos t sin 240o 


3
3
C1 I 2m sin 2 t  
C1 I 2m 1  cos 2t 
2
4

(2.47)

Lực điện động tác động lên dây dẫn 1 chiếu lên trục y cũng được xác định theo
cách tương tự:
54


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN
F1y  F12 Y  F13Y

 







 C1 I 2m sin t sin t  120o  sin t  240o sin 30 o



(2.48)

3
3
C1 I 2m sin t. cos t  
C1 I 2m sin 2t
2
4

Lực điện động tác động lên dây dẫn 1 sẽ là:
F1  F12x  F12y

(2.49)

Thay (2.47) và (2.48) vào (2.49) ta được:
3
2
C1 I 2m 1  cos 2t   sin 2 2t
4
3
3

C1 I 2m 21  cos 2t  
C1 I 2m sin t
4
2

F1 


(2.50)

Sự thay đổi về trị số và hướng của lực điện động tác động lên dây dẫn 1 có thể
được biểu diễn bằng véctơ OM mà quỹ tích của đầu cuối véctơ là đường trịn có đường
kính bằng

3
C1 I 2m (H2.9). lực điện động tác động lên các dây dẫn 2 và 3 cũng được
2

tính tốn tương tự như trong trường hợp của dây dẫn 1, chúng chỉ khác về góc lệch và
vị trí trong khơng gian.

2. Khi dịng điện xoay chiều có chứa thành phần khơng chu kỳ
Khi trong hệ thống điện ba pha có xảy ra sự cố ngắn mạch. Dòng điện tăng lên
về trị số và trong thành phần của chúng xuất hiện các thành phần không chu kỳ. Chúng
được biểu diễn dưới dạng:


e
e



i 1  I m e  R / Lt cos   cost  

i2  Im

i3  Im




 R / Lt

cos(  120 )  cos t    120o

 R / Lt

cos(  240 cos t    240

o

o



trong (2.51):  - góc pha khi bắt đầu xảy ra sự cố.

55

o





(2.51)



Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Việc khảo sát sự biến thiên của lực điện động trong trường hợp này cũng được
tiến hành giống như trong trường hợp khi dòng điện biến thiên điều hòa. Ta có thể thấy
rõ ảnh hưởng của thành phần
khơng chu kỳ lên lực điện
động như trong (H2.10)
Giá trị cực đại của lực
điện động ở đây phụ thuộc vào
thời điểm xảy ra ngắn mạch.
Việc tính tốn lực điện động
được tiến hành theo phương
pháp đơn giản hóa. Kết quả
tính tốn sẽ lớn hơn so với giá
trị thực tế, do đó có thể làm
tăng độ an toàn đối với thiết bị
thiết kế theo giá trị này. Ở đây
ta giả thiết rằng dòng điện
trong các pha đối xứng và có
biên độ bằng giá trị dịng điện
xung kích. Lực đẩy lớn nhất
tác động lên dây dẫn 1.
F1d max  0,805C1i 2XK  0,805C1 K XK I m 

2

(2.52)

trong đó: iXK - dịng điện xung kích; KXK - hệ số dịng điện xung kích.
Lực điện động tác động khi dây dẫn ở pha giữa:

 F2d max  F2 h max  0,866C1 K XK .I m 

2

(2.53)

2.2 LỰC HÚT ĐIỆN TỪ
1. Xác định lực hút điện từ theo công thức Maxwell
Đối với các trường hợp, mà ở đó lực tác động chỉ lên phần tử mang dịng điện và
nó có hình dạng đơn giản, thì phương trình (2.4) nói chung được áp dụng dễ dàng và
đơn giản nhất để tính lực tác động trong hệ thống. Có rất ít trường hợp thực tế như vậy.
Trên thực tế, phần lớn các thiết bị biến đổi điện cơ đều có mang các vật thể dẫn từ. trong
các hệ thống này, lực tác động trực tiếp lên vật thể dẫn từ, tất nhiên ta khơng thể sử dụng
phương trình (2.4) để tính tốn.
Tính tốn các lực nội bộ và thành phần tác động lên các vật thể dẫn từ rất phức
tạp và địi hỏi phải có sự hiểu biết về phân bố trường trong kết cấu thiết bị. Rất may là
tất cả các thiết bị biến đổi điện - cơ được cấu tạo một cách bền vững và không hề bị biến
dạng dưới tác động của lực.
Để phân biệt với lực điện động ta gọi lực tác động lên các vật thể dẫn từ là lực
hút điện từ. Một trong các phương pháp cơ bản để xác định lực hút điện từ là phương
pháp theo cơng thức của Maxwell. Nó xác định mối liên hệ giữa lực hút điện từ, từ thơng
và kích thước cực từ theo quan hệ sau:
Fdt 

1
o

 B .n B





S





1 2 
B  .n dS
2


trong đó:Ġvector từ cảm trên bề mặt cực từ
Ġ vector đơn vị pháp tuyến trên bề mặt cực từ
s diện tích bề mặt cực từ
56

(2.54)


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Công thức (2.54) được sử dụng đối với trường hợp khi từ thông phân bố không
đều trong khe hở không khí và khi vector từ cảmĠkhơng vng góc với bề mặt cực. Bề
mặt cực từ (nơi tác động của lực hút điện từ) là bề mặt phana chia giữa hai mơi trường


có dộ từ thẩm rất khác nhau ( và o). nếu <<o thì góc giữa vectơ pháp tuyến n và





vectơ từ cảm sẽ khơng lớn, vì vậy cho rằng hai vectơ n và B trùng phương với nhau.
Trong trường hợp đó cơng thức (2.54) sẽ trở nên đơn giản hơn:
Fdt 

1
B 2 dS

2 o S

(2.55)

Nếu từ cảm không thay đổi trên tồn bộ bề mặt cực từ, có nghĩa là từ thông phân
bố đều trong khu vực khe hở khơng khí, thì có thể đơn giản hóa cơng thức tính lực sau:
Fdt 

1
B 2 .S
2 o

(2.56)

Nếu 0 = 4 .10-7 (H/m); B tính ra Tesla (Wb/m2); S tính ra m2.
Ta có thể viết: Fdt  39,8.104 B2 .S (N)
(2.57)
4 2
Hoặc:
(2.58)

Fdt  4,06.10 B .S (Kgf)
Sự phân bố đều của từ thơng trong khe hở khơng khí có thể nhận được ở một vài
trường hợp hãn hữu, ví dụ như ở trong khe hở giữa hai cực từ hình trụ có tỷ lệ /d  0,2
(d là đường kính cực từ,  độ lớn của khe hở). Trong phần lớn các trường hợp cịn lại,
nói chung từ thơng phân bố khơng đều. Trong các trường hợp đó, nếu áp dụng cơng thức
(2.56), (2.57), (2.58) để tính lực hút điện từ sẽ dẫn đến sai số đáng kể.
2. Lực hút điện từ xoay chiều
Lực hút điện từ xoay chiều có thể xác định theo công thức Maxwell. Trong trường
hợp này phải chú ý từ thông là đại lượng biến thiên tuần hồn về độ lớn và về phương.
Giả sử, từ thơng biến thiên theo luật hình sin:
 = msint
(2.59)
khi đó lực hút điện từ tính theo Maxwell sẽ là:
Fdt  4,06.10  4

do: sin 2 t 

 2m
sin 2 t
S

(2.60)

1  cos 2t
, nên khi thay vào công thức (2.60) ta nhận được:
2
2
2
4 m
4 m

Fdt  2,03.10
 2,03.10
cos 2t  F  F2
S
S

(2.70)

trong đó: F= - Thành phần lực khơng thay đổi theo thời gian
F2- Thành phần biến thiên theo thời gian với tần số gấp đôi tần số của từ
thông xoay chiều.
Đồ thị biểu diễn các thành phần của lực xoay chiều được trình bày trong (H2.11).
Từ các đồ thị nhận được, có thể rút ra các kết luận sau:
- Lực hút điện từ xoay chiều có dạng đập mạch, trong một chu kỳ của điện áp
nguồn có hai lần lực giảm xuống trị số zero. (đập mạch với tần số gấp hai lần tần số của
nguồn điện).

57


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

- Giá trị trung bình của lực hút điện từ xoay chiều trong một chu kỳ đúng bằng
giá trị của thành phần khơng đổi F= của nó, tức là:
 2m
Ftb  F  2,03.10
S
4

(2.71)


- Để xác định toàn bộ các thành phần của lực hút điện từ xoay chiều, ta chỉ cần
xác định được giá trị trung bình của lực sau đó dùng quan hệ (2.70) để thành lập biểu
thức tính lực hút điện từ xoay chiều.
3. Biện pháp giảm rung nắp ở nam châm điện xoay chiều một pha
Giá trị tức thời của lực hút điện từ xoay chiều trong một chu kỳ có hai lần giảm
xuống trị số zero. Tại các thời điểm này dưới tác động của hệ thống phản lực của cơ cấu
(lò xo nhả nắp của nam châm điện...) nắp của nam châm điện bị kéo ra xa khỏi cực từ
hút nó và sau đó khi lực hút điện từ lại đạt giá trị lớn hơn lực của hệ thống phản lực, nắp
lại được hút về phía cực từ (H2.12). Hiện tượng trên được gọi là hiện tượng rung nắp ở
nam châm điện xoay chiều. Để loại trừ hiện tượng rung, trong nam châm điện xoay
chiều 1 pha phải tạo ra ở bên trong khe hở khơng khí  hai từ thơng lệch pha nhau. Có
thể áp dụng các biện pháp sau, để thực hiện việc làm giảm rung nắp nam châm điện
xoay chiếu.
1- Chia mạch từ ra làm hai phần, mỗi phần đều có cuộn dây riêng và tạo ra sự
lệch pha giữa các dịng điện trong các cuộn dây đó.
2- Đặt vịng ngắn mạch, ơm lấy một phần cực từ tại vị trí khe hở khơng khí.
Biện pháp thứ 2 có ưu điểm hơn hẵn so với biện pháp thứ 1 do việc thực hiện đơn
giản, rẻ tiền, vì vậy nó được áp dụng rộng rải trong các NCĐ một pha.
Hình 2.12: biểu diễn mạch từ một pha trên lõi có đặt vịng ngắn mạch. Từ thông
 do cuộn dây xoay chiều sinh ra, khi đi qua vùng khe hở khơng khí bị chia ra làm hai
thành phần 1 và 2 do ảnh hưởng của vịng ngắn mạch. Từ thơng 2 đi xun qua
vịng ngắn mạch gây cảm ứng bên trong nó một sức điện động Enm có xu hướng chống
lại từ thơng 2 (theo luật Lenz). Hay nói một cách khác, dịng điện chảy trong vòng
ngắn mạch l = Enm/rnm (với rnm là điện trở của vòng ngắn mạch) sẽ sinh ra từ thông nm
ngược chiều với từ thông 2 và làm cho 2 chậm pha so với 1.
Đối với một cực từ có vịng ngắn mạch, tổng lực hút điện từ tác động lên cực từ
đó sẽ là:

58



Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

F  F1  F2
  12

 22
2
 4,06.10 
sin t 
sin 2 (t  )
S2
 S1

2
2
2

 2m 
 22 m
4   1m
4   1m




 2,03.10 



2
,
03
.
10
cos
2

t

cos
2

t

2



S 2 
S2
 S1
 S1

4

(2.72)

Từ biểu thức (2.72) có thể biểu diễn tổng lực hút điện từ tác động lên cực từ theo
cách khác, như sau:

F  F  F2
(2.73)
trong đó:

 2
2 
F  2,03.10 4  1m  2 m  là thành phần không biến đổi theo thời gian.
S2 
 S1
2

 22 m
4   1m

F2  2,03.10 
cos 2t 
cos(2t  2  là thành phần biến thiên
S2
 S1


theo thời gian với tần số gấp đôi tần số của lưới điện.
 là góc lệch pha giữa hai từ thơng 1 và 2.

Hình 2.13 biểu diễn các giá trị của lực theo thời gian. Ta thấy rằng, tổng lực hút
điện từ xoay chiều, khơng cịn có điểm nào bị giảm xuống trị số zero nữa. Điều này có
thể đảm bảo cho nam châm điện xoay chiều khơng cịn bị rung nắp nữa nếu như giá trị
cực tiểu Fmin của tổng lực F ở biểu thức (2.73) luôn lớn hơn tổng phản lực của hệ thống
Ffl.
Fmin > Ffl

(2.74)
Từ biểu thức về F2 trong (2.73) nhận thấy rằng:
Nếu như: 1 = 2; S1 = S2 và góc lệch pha  = 90 thì thành phần F2 = 0, có nghĩa
là tổng lực:
 2
2
F  F  2,03.10 4  1m  2 m
S2
 S1






(2.75)

Nhưng, trên thực tế một điều kiện như vậy khơng thể thực hiện được vì:
tg 

X nm .G  2

R 2
rnm

(2.76)

Ở đây: Xnm từ kháng của vòng ngắn mạch, nó được xác định từ (1.90);
R2 từ trở của phần khe hở khơng khí có đặt vịng ngắn mạch. Từ (2.76) thấy
rằng, muốn đạt được điều kiện:  = 90 thì: tg =  ; khi  = const và G2 = const, điều

này chỉ có thể đạt được rnm = 0 hay nói một cách khác phải tìm ra được vật liệu dẫn điện
có điện trở suất bằng zero.
Các trị số cực đại và cực tiểu của lực hút xoay chiều tổng có thể tính được:
59


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Fmax  F  F

(2.77)

Fmin  F  F

(2.78)

Trong các cơng thức (2.77) và (2.78): F chính là biên độ của thành phần biến
thiên theo thời gian của lực hút điện từ xoay chiều. Nó chính bằng giá trị đường chéo
của hình bình hành có cạnh là các vector lực xoay chiều sinh ra các từ thông 1 và 2
(H2.14).
F  F12  F22  2F1 .F2 . cos 2
(2.79)
trong đó:

F1  2,03.104

12m
S1

(2.80)


F2  2,03.10 4

 22 m
S2

(2.81)

Đối với các cơ cấu điện từ xoay
chiều, đại lượng quan trọng có ý nghĩa
quyết định là Fmin. để loại trừ sự rung nắp
khi nó hoạt động cần phải đảm bảo điều
kiện duy nhất Fmin > Ffl. Giá trị của Fmin theo
Stupel có thể nhận được từ các điều kiện
sau:


S1 2  f 3

S
4f 3

rnm 

(2.82)

 o .S 2
4f 3
.
2

3f 3  22

(2.83)

trong các công thức (2.82) và (2.83):
f3 

K 4 Ff l
Ftb

(2.84)

với Ftb và Ffl là lực điện từ trung bình và phản
lực của hệ thống (Kgf); k4 = (1,1  1,2) là hệ
số tin cậy; S = S1 + S2 là diện tích cực từ; S2
là diện tích cực từ trên đó có đặt vịng ngắn
mạch; 2 là độ lớn khe hở khơng khí ở phần
cực từ có đặt vịng ngắn mạch.
Sau khi đã chọn được  và rnm có thể
dễ dàng xác định góc lệch pha giữa hai từ
thơng từ biểu thức (2.76).
Tỷ số giữa hai từ thông 1 và 2 sẽ là:
2F1 .G 1
1

2
2F2 G  2

(2.85)
Từ đồ thị trong (H2.15) biểu diễn mối liên hệ giữa các vector 1, 2, F1, F2 (là

các sức từ động sinh ra các từ thơng 1 và 2, ta có: F2 = F1.cos, từ đó khi thay vào
(2.85) sẽ được:
1
S1

 2 S 2 . cos 

(2.86)
60


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

mặt khác ta có:  2  12   22  2.12 . 22 . cos 
thay (2.86) vào (2.87) nhận được:
2 



1  C  2C. cos 
2

(2.87)
(2.88)

Sau khi tính các giá trị từ thơng theo (2.88) thay vào trong các biểu thức (2.80)
và (2.81) ta sẽ tính được các giá trị lực F1=, F2= và theo (2.79) sẽ nhận được giá trị F
và cuối cùng ta tính được Fmin theo (2.78).
2.3 SỰ CÂN BẰNG NĂNG LƯỢNG
Nguyên lý bảo tồn năng lượng phát biểu rằng năng lượng khơng tự nhiên sinh

ra và mất đi, nó chỉ biến đổi từ dạngnày sang dạng khác. Ví dụ một trái banh golf rời
khỏi cây đánh golf với một động năng nhất định, năng lượng này cuối cùng tiêu tán ớiii
dạng nhiệt là do có ma sát giữa trái banh với khơng khí và ma sát lăn khi trái banh bay
trên khơng trung và khi nó lăn trên thảm cỏ. Tương tự như vậy, động năng của cái búa
cuối cùng cũng tiêu tán dưới dạng nhiệt khi cái đinh được đóng sâu vào một vật nào đó.
Trong các hệ thống điện cơ có thể tính tốn sự biến đổi năng lượng chủ yếu dựa
vào năng lượng dự trữ trong từ trường.
Năng lượng
Độ gia tăng năng
Năng lượng
Cơ năng
nhận từ
lượng dự trữ trong
biến thành
(2.89)
=
đầu ra +
+
nguồn điện
từ trường
nhiệt
Phương trình (2.89) được viết sao cho, các phần điện và cơ năng có giá trị dương
cho các hoạt động của motor. Phương trình này cũng áp dụng cho hoạt động của các
máy phát khi đó các số hạng tương ứng ở vế phải đều có giá trị âm. Trong các hệ thống
này, sự biến đổi năng lượng sang dạng nhiệt xảy ra theo cơ chế giống như tổn hao đồng
do dòng điện chạy trong cuộn dây ở đầu vào, và ma sát cơ do sự chuyển động của các
thành phần trong cơ cấu đầu ra cơ của hệ thống.
1. Tính lực điện động bằng phương pháp cân bằng năng lượng
Nếu bỏ qua năng lượng tĩnh điện và coi lực điện động tác động không làm cho
dây dẫn bị biến dạng mà chỉ làm cho nó dịch chuyển, đồng thời dịng điện chyạ trong

dây dẫn là khơng đổi, thì lực điện động được xác định theo:
F

A
x

(2.90)

trong đó: A - năng lượng điện từ của hệ thống;
x - độ dịch chuyển của dây dẫn theo hướng tác động của lực.
Như vậy: Lực điện động theo quan điểm cân bằng năng lượng bằng đạo hàm
riêng của năng lượng điện từ trong hệ thống mạch vòng dẫn điện lấy theo độ dịch
chuyển của hệ thống theo hướng tác động của lực.
Năng lượng điện từ trong hệ thống mạch vòng dẫn điện bao gồm năng lượng điện
từ dự trữ riêng trong từng mạch vòng và năng lượng điện từ tương hỗ giữa các mạch
vịng với nhau. Ví dụ, năng lượng điện từ của hệ thống hai mạch vòng dẫn điện nằm bên
cạnh nhau bằng:
1
1
A  L 1i 12  L 2 i 22  M 12 i 1 .i 2
2
2

(2.91)

trong đó: L1, L2 - tự cảm của mạch vòng 1 và 2
i1, i2 - dòng điện chạy trong các mạch vòng 1 và 2
M12 - hỗ cảm giữa các mạch vòng 1 và 2
61



Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Hai số hạng đầu ở vế phải của (2.91) biểu diễn năng lượng điện từ riêng dự trữ trong
mỗi mạch vòng độc lập, còn số hạng thứ ba biểu diễn năng lượng điện từ tương hỗ giữa
chúng với nhau.
Xác định lực nội bộ của một mạch vòng theo:
Fnb 

A 1 2 L
 i
x 2 x

(2.92)

vì ta đã giả thiết rằng, năng lượng điện từ thay đổi dẫn đến sự thay đổi vị trí tương đối
giữa các mạch vịng. Do đó, năng lượng do tự cảm sinh ra là không đổi và lực điện động
tương tác giữa các mạch vòng được tính như sau;
F

M 12
A
 i 1 .i 2
x
x

(2.93)

Nếu biết được hàm giải tích của tự cảm, hoặc hỗ cảm theo các thơng số hình học của
mạch vịng, thì sử dụng phương pháp cân bằng năng lượng để tính lực điện động rất

thuận lợi. Phương pháp này cũng cho khả năng xác định hướng tác động của lực điện
động. Từ (2.90) suy ra rằng, năng lượng điện từ của hệ thống tăng lên có nghĩa làĠ
tương ứng với chiều dương của lực và ngược lại.
2. Xác định lực hút điện từ nhờ cân bằng năng lượng
Khi đóng cuộn dây nam châm điện vào một mạch điện có điện áp u. Quá trình
q độ trong cuộn dây được mơ tả bằng phương trình quen thuộc:
u  iR 

d
dt

(2.94)

trong đó: i dịng điện chạy trong cuộn dây;
R- điện trở cuọn dây; và  - từ thơng móc vịng.
Nếu nhân cả hai vế của phương trình (2.94) với i.dt, ta có thể nhận được biểu
thức mô tả sự cân bằng năng lượng trong nam châm điện:
u.i.dt  i 2 Rdt  i.d
(2.95)
vế trái của (2.95) là năng lượng mà nam châm điện nhận được từ nguồn trong thời gian
dt. Thành phần thứ nhất bên vế phải của phương trình là tổn hao đồng trong cuộn dây.
Thành phần thứ hai id( là gia số năng lượng từ trường trong nam châm điện. Tổng năng
lượng từ trường có dạng:


W   id

(2.96)

0


Trong các thành phần năng lượng của (2.95) ta nhận thấy rằng, thành phần tương
ứng với (2.96) là thành phần sinh ra công cơ học, gây ra sự chuyển động của nắp nam
châm điện.

62


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Quan hệ   f i  trong trường hợp tổng quát mang tính phi tuyến. Đối với các giá
trị khác nhau của khe hở khơng khí , quan hệ này cho các đặc tính khác nhau. Khi 
lớn
  f i  thường ít dốc hơn so với  bé (H2.16) mơ
tả các đặc tính   f i  khi  thay đổi. Ở giá trị 
= 1, khi dòng điện trong cuộn dây tăng đến giá
trị i1, khi đó nắp của nam châm điện bắt đầu
chuyển động.
Đối với vị trí của nắp nam châm điện
tương ứng với  = 1. Năng lượng từ trường dự
trữ trong nam châm điện tỷ lệ với diện tích
Soabo:
1

W   id  S abcda

(2.97)

0


Khi nắp chuyển động quan hệ , i diễn
biến khá phức tạp. Nguyên nhân là do tự cảm L
của hệ thống thay đổi, sinh ra sức phản điện động
trong cuộn dây, có chiều ngược với điện áp
nguồn. Sức phản điện động này làm cho dòng
điện trong cuộn dây giảm từ 1 xuống 2. Năng
lượng từ trường trong nam châm điện tăng thêm
một lượng bằng:
2

 id  S

abcda

1

(2.98)
Tại vị trí  = 2, năng lượng từ trường có giá trị:
2

W   id  S ocdo
0

(2.99)
Suy ra, khi  biến thiên từ 1 đến 2 năng lượng
từ trường trong nam châm điện biến thiên một
lượng bằng:
W  S oabo  S abcda  S ocdo  S obco

(2.100)

Sự biến thiên này của năng lượng từ trường, chính là nguyên nhân gây ra công
cơ học làm cho nắp chuyển động. Vì vậy, nó phải cân bằng với cơng cơ học thực hiện
việc làm cho nắp nam châm điện chuyển động một đoạn đường:
(2.101)
  1   2
Khi đó ta có thể viết biểu thức của cơng cơ học:
A  F.  W
(2.102)
Ở đây: F - giá trị trung bình của lực hút trên đoạn  từ (2.102) ta có:
Fdt 

W
 W  dW
 lim


   d

(2.103)

63


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Suy ra rằng, để xác định lực hút điện từ theo phương pháp cân bằng năng lượng,
trước hết phải xây dựng các đường cong   f i  ở các giá trị khác nhau của . Sau đó
áp dụng (2.103) để tính giá trị của lực. Đối với các hệ thống mạch từ chưa bị bảo hòa,
quan hệ   f i  có dạng tuyến tính, và khi nắp nam châm điện chuyển động chậm,
(không xảy ra hiện tượng sức phản điện động), thì dịng điện trong cuộn dây sẽ tồn tại

không thay đổi và lực hút điện từ có thể tính được từ biểu thức đơn giản. Thật vậy, từ
đồ thị (H2.17) dễ dàng rút ra được:
W 

1
1
1
 1 I  I 2   1    2 J  I
2
2
2

(2.104)

trong đó: 
Áp dụng (2.103) ta nhận thấy được biểu thức tính lực như sau:
 W  1 d
Fdt  lim
 I
   2 d

(2.105)

trong biểu thức (2.105), nếu 0 = 4.109 (H/cm), các kích thước tính ra cm, thì lực hút
điện từ có thứ nguyên là (J/cm).
Ta biết rằng 1J/cm = 100 N
Khi đó, cơng thức (2.105) có thể được viết dưới dạng
Fdt  5,1.I.

d

(Kgf)
d

(2.106)

Đối với nam châm điện xoay chiều (AC), cuộn dây mắc song song, khi khe hở
khơng khí thay đổi, từ thơng móc vịng:
 = N. = Const
Chỉ có s.t.đ IN thay đổi. Dễ dàng thấy rằng, trong trường hợp này sự biến thiên
của năng lượng từ trường chính là diện tích tam
giác obc (H2.18):
W 

1
1
1
i 1  i 2  i
2
2
2

(2.107)
Fdt 

suy ra:

1 di

2 d


(2.108)
nếu:



1
2

N; i 

Thay các giá trị  và


2 N.G 

;

dG 
di


.
d
2.N.G 2 d

di
vào biểu thức (2.108) ta nhận được biểu thức tính lực hút điện
d

từ:

Fdt  

dG
1
IN 2 . 
2
d

(2.109)

trong đó: G- tương đương của các khe hở khơng khí trong mạch từ. dấu âm trogn biểu
thức cho thấy rằng đạo hàm của từ dẫn theo  mang dấu âm (quan hệ G =f() được biểu
diễn bằng đường cong Hyperbol).
Có thể biểu diễn biểu thức tính lực theo cách sau:
64


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Fdt 

dG
1
IN 2 
2
d

(2.110)

trong đó: nếu Gtính ra (H/m) thì lực Fđt tính ra Newton (N).

2.4 CÁC PHƯƠNG TRÌNH ĐỘNG
Chúng ta đã có các biểu thức về lực
tính ra trong các thiết bị biến đổi năng
lượng điện - cơ. Chúng là hàm số của các
biểu số về điện và về sự chuyển động cơ
khí. Các biểu thức được rút ra đối với các
hệ thống bảo tồn năng lượng. Trong đó,
bất cứ tổn hao nào cũng đều thuộc về các
nguồn điện và cơ. Các thiết bị biến đổi
năng lượng hoàn toàn có thể hoạt động hai
chiều, giữa một hệ thống điện và một hệ
thống cơ.
Mơ hình của một hệ thống biến đổi
đơn giản được trình bày trong (H2.19). Hệ thống được trình bày bao gồm ba phần:
1. Một hệ thống điện ở đầu vào.
2. Bộ biến đổi năng lượng trung gian
3. Hệ thống cơ khí ở đầu ra
Hệ thống điện được biểu diễn bằng một nguồn điện áp U và điện trở. Nó cũng có
thể là nguồn dịng điện và một điện dẫn G song song. Phương trình điện sẽ là:
U  iR 


dt

(2.111)

Nếu từ thơng móc vịng  có thể được biểu diễn bằng biểu thức  = L(x).i từ đó
phương trình nguồn điện ngồi, sẽ có dạng:
U  iR  L( x )


dL ( x ) dx
di
i
.
dt
dt
dt

(2.112)

đại lượng L.(di/dt): điện áp tự cảm; i(dL(x)/dt) điện áp cảm ứng do tốc độ chuyển động.
Hệ thống cơ trong (H2.19) trình bày các biểu tượng của một lị xo (có hệ số lò xo
là K), một bộ đệm (với hệ số đệm B), một khối lượng M và một lực cơ học kích thích
từ bên ngồi fo. lực và độ dịch chuyển x có liên quan với nhau theo:
Lị xo:
fK = K( x - xo )
(2.113)
Đệm:
fD = B(dx/dt)
(2.114)
Khối lượng: f M

d2x
M 2
dt

(2.115)

Trong đó xo là độ nén ban đầu của lị xo.
Khi có lực tác động lên hệ thống, lực cân bằng sẽ là:

2

d x
dx
F  f K  f D  f M  f o  K x  x o   B  M 2
dt
dt

(2.116)

Các phương trình vi phân đối với toàn bộ hệ thống trong (H2.19) và đối với các đại
lượng đầu vào Vo(l) và fo sẽ là:
dL ( x ) dx
di
i
.
dt
dx dt
d2
dx
f o (t )  M x2  B
 K(x  x o )  F(x, i)
dt
dt
U  iR  L( x )

65

(2.117)
(2.118)



Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

Các hàm số L(x) và F(x,i) phụ thuộc vào đặc điểm của thiết bị biến đổi năng
lượng.
2.5 LỰC VÀ NGẪU LỰC TRONG CÁC HỆ THỐNG VỚI NCVC
Các biểu thức tính lực và ngẫu lực trong các mục trước được rút ra khi cho rằng
từ trường trong các hệ thống dự trữ năng lượng có được là do sự kích từ bởi dòng điện
chảy trong cuộn dây đặc biệt trong hệ thống, và lực được tính bằng giá trị của đạo hàm
năng lượng từ trường dự trữ trong hệ thống theo độ dịch chuyển của phần chuyển động
của hệ thống.
Trong các hệ thống với nam châm vĩnh cửu điều này phải được xem xét một cách
kỹ lưỡng.
Trong một vài trường hợp hệ thống với NCVC có thể khơng có bất kỳ một cuộn
dây nào cả. Từ trường có được ở đây là do sự có mặt của vật liệu NCVC. Khi đó ta
khơng thể nói về từ thơng móc vịng và dòng điện cuộn dây.
Trong một vài trường hợp khác từ trường có thể được sinh ra do sự kết hợp giữa
NCVC và cuộn dây.
Một sự biến thể của các phương pháp đã giới thiệu trong các mục khác có thể sử
dụng trong hệ thống với NCVC. Bản chất của phương pháp này là việc cho rằng trong
hệ thống có cuộn dây tưởng tượng phụ tác động trên cùng một phần của mạch từ của
NCVC. Trong các điều kiện hoạt động bình thường cuộn dây này có dịng điện bằng
zero. Chức năng của cuộn dây tưởng tượng chỉ đơn thuần về phương diện tốn học khi
cần phải hồn thiện một sự phân tích cần thiết nào đó. Dịng điện trong cuộn dây này có
thể được điều chỉnh về giá trị zero.
Nhằm mục đích tính tốn năng lượng của hệ thống cuộn dây giả định (tưởng
tượng) cũng được xem như các cuộn dây bình thường khác, có nghĩa là nó cũng có dịng
điện và từ thơng móc vịng riêng. Kết quả là các biểu thức về năng lượng nhận được
cũng sẽ là hàm của

dịng điện I và từ thơng
móc vịng .
H2.20a: mơ tả
một mạch từ với
NCVC và một nắp
theo vị trí của nắp, ta
cho rằng có một cuộn
dây giả định với Nf
vịng dây, nó mang
dịng điện If và được
quấn nối tiếp với
NCVC như được trình
bày trong H2.20b.
Đối với hệ thống cuộn dây kích từ đơn ta có thể viết biểu thức đối với vi phân
đồng năng lượng như sau:
dW ' i f , x    f di f  F.dx
(2.119)

66


Chương 2- CÁC NGUYÊN LÝ BIẾN ĐỔI NĂNG LƯỢNG CƠ BẢN

ký hiệu f chỉ cuộn dây giả định. Tương tự như ở (2.103) lực trong hệ thống này có thể
được viết như sau:
if

dW i f  0, x 
F
dx


(2.120)
Ở đây đạo hàm được lấy khi cho if
bằng hằng số và kết quả được lấy khi if =0.
Để tính đồng năng lượng W (if = 0,x)
trong hệ thống cần phải lấy tích phân phương
trình (2.19) và do W’ (if,x) là một hàm trạng
thái ta hoàn toàn tự do lựa chọn đường lấy
tích phân nào mà ta muốn. (H2.21) minh họa
một đường, qua đó có thể lấy tích phân tương
đối đơn giản. Đối với nó có thể viết biểu thức
về đồng năng lượng của hệ thống như sau:
W ' i f  0, x  



dæång1a
x

 dW

dW ' 

If0

1b

0






0

  F i f  I fo , x dx    f i f , x di f
0

x

x’

Hình 2.21

'

duong1b
,

1a

(2.121)

'

I fo

ta bắt đầu lấy tích phân từ điểm A, đây là một điểm rất đặc biệt trong hình, nó
tương ứng với dịng điện Ifo trong cuộn dây giả định, tại đó năng lượng dự trữ trong hệ
thống bằng zero và tại đó cả từ thơng móc vịng f và lực F tác động lên nắp đều bằng

zero. Nói cách khác, dịng điện Ifo là dịng điện trong cuộn dây giả định, nó bao gồm cả
từ trường do NCVC sinh ra. Bởi vì lực bằng zero khi If = Ifo, tích phân qua đường 1a
trong (2.121) bằng zero và dẫn đến.
0

W ' i f  0, x     f i f , x di f

(2.122)

I fo

Chú ý: phương
trình (2.122) là tổng qt
nó khơng địi hỏi phải có
NCVC. Khi đã xác định
được đồng năng lượng từ
(2.122), lực tại vị trí nắp
cho trước x có thể tìm
được theo (2.120). Vì sự
có mặt của NCVC, cả
đồng năng lượng W’ = (if
= 0,x) và lực F đều khác
zero khi if = 0. Điều đó
nói lên sự có mặt của NCVC.
Đồng năng lượng được định nghĩa như là một hàm số của dòng điện cuộn dây i
vị trí của nắp nam châm điện x. Nó có giá trị bằng:
W ' i, x   i.  W, x 
(2.123)
Điều này được minh họa bằng đồ thị trên (H2.22). Nếu năng lượng từ trường tỷ
lệ với diện tích SOBCO trong (H2.22), thì đồng năng lượng tỷ lệ với diện tích SOABO.

67