BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
---------------

NGUYỄN THỊ NGỌC XUÂN

ĐIỀU KHIỂN TRƯỢT VÀ ỨNG DỤNG
Chuyên ngành: Điều khiển và tự động hóa

LUẬN VĂN THẠC SĨ KHOA HỌC
ĐIỀU KHIỂN VÀ TỰ ĐỘNG HÓA

NGƯỜI HƯỚNG DẪN KHOA HỌC
PGS.TS. PHAN XUÂN MINH

HÀ NỘI - 2012


MỤC LỤC

Lời cam đoan...............................................................................................................3
DANH MỤC CÁC HÌNH VẼ, ĐỒ THỊ .....................................................................4
MỞ ĐẦU.....................................................................................................................6
CHƯƠNG 1. PHƯƠNG PHÁP ĐIỀU KHIỂN TRƯỢT.......................................8
1.1. Vài nét về lịch sử điều khiển trượt ............................................................................8
1.2. Cơ sở lý thuyết điều khiển trượt [3] ..........................................................................9
1.2.1.Điều khiển đối tượng tích phân kép ........................................................................9
1.2.2. Nguyên tắc chung của điều khiển trượt ...............................................................14
1.3. Đặc tính bền vững của điều khiển trượt [2] ............................................................15
1.3.1. Bộ điều khiển trượt ổn định bền vững .................................................................15
1.3.2. Bộ điều khiển trượt bám bền vững .......................................................................19

1.4. Hiện tượng rung (chattering) trong điều khiển trượt .............................................20
1.4.1. Phương pháp lớp biên để làm giảm hiện tượng chattering ...............................21
1.4.2. Phương pháp dùng hàm chuyển mạch tích phân bão hồ sat-PI .....................23
1.5. Kết luận .......................................................................................................................23
CHƯƠNG 2. THIẾT KẾ BỘ ĐIỀU KHIỂN TRƯỢT VÀ BỘ QUAN SÁT
TRƯỢT ....................................................................................................................25
2.1. Thiết kế bộ điều khiển trượt .....................................................................................25
2.1.1. Mặt trượt ..................................................................................................................25
2.1.2. Bộ điều khiển trượt [11] ........................................................................................26
2.1.3. Ví dụ thiết kế bộ điều khiển trượt.........................................................................30

1


2.2. Bộ quan sát trượt (Sliding Mode Obsever - SMO) ................................................32
2.2.1. Khái niệm quan sát trạng thái ...............................................................................32
2.2.2. Vài nét khái quát về SMO .....................................................................................33
2.2.3. Thiết kế bộ quan sát trượt ......................................................................................34
CHƯƠNG 3. ỨNG DỤNG BỘ QUAN SÁT TRƯỢT VÀO ĐIỀU KHIỂN
ROBOT PLANAR HAI BẬC TỰ DO...................................................................38
3.1. Mơ hình tốn học của Robot Planar hai bậc tự do .................................................38
3.1.1. Phương trình Euler - Lagrange ............................................................................38
3.1.2. Xây dựng phương trình động lực học ..................................................................38
3.1.3. Các đặc tính động học robot..................................................................................43
3.1.4. Mơ tả toán học robot planar hai bậc tự do trong không gian trạng thái...........43
3.2. Thiết kế bộ điều khiển trượt cho robot ....................................................................45
3.3. Ứng dụng bộ quan sát trượt điều khiển robot .......................................................47
3.3.1. Thiết kế bộ quan sát trượt ......................................................................................47
3.3.2. Điều khiển dựa vào bộ quan sát trượt ..................................................................49
3.4.1. Xây dựng các sơ đồ mô phỏng..............................................................................49

3.4.2. Kết quả mô phỏng ..................................................................................................56
3.5. Nhận xét, đánh giá kết quả mô phỏng .....................................................................63
KẾT LUẬN ...............................................................................................................65
TÀI LIỆU THAM KHẢO.........................................................................................66
PHỤ LỤC..................................................................................................................68

2


Lời cam đoan

Tôi xin cam đoan luận văn thạc sĩ với đề tài “Điều khiển trượt và ứng
dụng” do tôi tự thực hiện dưới sự hướng dẫn của cô giáo PGS.TS. Phan Xuân
Minh. Các số liệu và kết quả hoàn toàn trung thực.
Ngoài các tài liệu tham khảo đã dẫn ra ở cuối luận văn, tôi đảm bảo rằng
không sao chép các cơng trình hoặc kết quả của người khác. Nếu phát hiện có sự sai
phạm với điều cam đoan trên, tơi xin hồn tồn chịu trách nhiệm.

Học viên

Nguyễn Thị Ngọc Xuân

3


DANH MỤC CÁC HÌNH VẼ, ĐỒ THỊ

Hình 1.1. Thiết kế bộ điều khiển trượt cho đối tượng tích phân kép........................10
Hình 1.2. Quỹ đạo sai lệch trạng thái và hiện tượng trượt về gốc tọa độ .................12
Hình 1.3. Điều khiển trượt đối theo ngun tắc phản hồi tín hiệu ra .......................13

Hình 1.4. Điều khiển trượt bám đối tượng tích phân kép .........................................14
Hình 1.5. Bộ điều khiển trượt ổn định bền vững ......................................................16
Hình 1.6. Hiện tượng chattering................................................................................21
Hình 1.7. Hàm bão hồ sat(s)....................................................................................22
Hình 1.8. Định nghĩa lớp biên B(t) ...........................................................................22
Hình 2.1, Hình 2.2, Hình 2.3.....................................................................................28
Hình 2.4. Mơ hình quan sát trạng thái.......................................................................33
Hình 2.5. Bộ quan sát trạng thái chế độ trượt ...........................................................35
Hình 3.2. Mơ tả hệ trục toạ độ của Robot .................................................................40
Hình 3.3. Mơ hình simulink của robot planar ...........................................................51
Hình 3.4. Sơ đồ simulink của hệ thống điều khiển trượt ..........................................51
Hình 3.5. Mơ hình simulink của bộ điều khiển trượt cho robot planar ....................52
Hình 3.6. Sơ đồ simulink tính giá trị trung gian tg1 .................................................53
Hình 3.7. Sơ đồ simulink tính giá trị trung gian tg2 .................................................53
Hình 3.8. Sơ đồ simulink của bộ quan sát trượt........................................................54
Hình 3.9. Sơ đồ simulink khảo sát bộ quan sát trượt ................................................55
Hình 3.10. Sơ đồ simulink hệ thống điều khiển kết hợp bộ quan sát trượt ..............55
Hình 3.11. Đáp ứng bộ quan sát với tác động mômen là các hàm bậc thang ..........57

4


Hình 3.12. Đáp ứng của bộ quan sát trượt với tác động mơmen là các hàm sin .....58
Hình 3.13. Đáp ứng vị trí khi sử dụng hàm sgn........................................................59
Hình 3.14. Đáp ứng vận tốc khi sử dụng hàm sgn....................................................59
Hình 3.15. Mơmen điều khiển khi sử dụng hàm sgn ................................................60
Hình 3.16. Đáp ứng vị trí khi sử dụng hàm sat .........................................................60
Hình 3.17. Đáp ứng tốc độ khi sử dụng hàm sat.......................................................61
Hình 3.18. Mơmen điều khiển khi sử dụng hàm sat .................................................61
Hình 3.19. Đáp ứng vị trí với hệ điều khiển sử dụng bộ quan sát trượt ...................62

Hình 3.20. Đáp ứng tốc độ với hệ điều khiển sử dụng bộ quan sát trượt .................62
Hình 3.21. Mơmen điều khiển với hệ điều khiển sử dụng bộ quan sát trượt............63

5


MỞ ĐẦU
Cùng với sự phát triển của khoa học và kỹ thuật, ngành điều khiển và tự
động hoá cũng đã có những bước tiến quan trọng. Những bước tiến đó đã góp phần
khơng nhỏ vào việc tăng năng suất lao động, giảm giá thành và nâng cao chất lượng
của sản phẩm. Theo quá trình phát triển của xã hội, nhu cầu nâng cao sản xuất và
chất lượng sản phẩm ngày càng đòi hỏi ứng dụng rộng rãi các phương pháp điều
khiển tự động. Với các hệ thống trong thực tế hầu hết là các hệ thống phi tuyến có
mơ hình và thông số bất định cũng như luôn chịu tác động của các nhiễu loạn bên
ngồi thì phương pháp điều khiển trượt là một trong những lựa chọn tốt nhất.
Phương pháp điều khiển trượt có ưu điểm lớn đó là rất đơn giản và có tính
bền vững cao. Trong thực tế nói chung và trong cơng nghiệp nói riêng có rất nhiều
đối tượng ứng dụng phương pháp điều khiển trượt bởi những ưu điểm của phương
pháp này, đặc biệt các đối tượng là robot.
Mơ hình động lực của Robot là mơ hình phi tuyến với nhiều tham số bất
định. Phương pháp tiếp cận đầu tiên để điều khiển các Robot là các phương pháp
điều khiển tuyến tính, các phương pháp thiết kế này có một số hạn chế đặc biệt đối
với Robot có đặc tính phi tuyến mạnh hoặc có tham số bất định . Chính vì vậy các
phương pháp điều khiển phải được tiếp tục nghiên cứu để đáp ứng được các yêu cầu
về chất lượng hoạt động của Robot.
Hệ thống điều khiển Robot đòi hỏi một cấu trúc điều khiển thay đổi linh hoạt
để đảm bảo tính ổn định và chất lượng bền vững khi có sự thay đổi các tham số của
mơ hình và khi có nhiễu tác động. Và vì vậy điều khiển trượt (Sliding Mode
Contrrol - SMC) hay cịn gọi là điều khiển có cấu trúc thay đổi (Variable Structure
System - VVS) là một phương pháp hiệu quả để giải quyết vấn đề này. Từ những

đánh giá nêu trên, tác giả luận văn đã quyết định lựa chọn đề tài “Điều khiển trượt
và ứng dụng”.
Nội dung luận văn được chia thành 3 chương với nội dung cơ bản như sau:
Chương 1. Phương pháp điều khiển trượt

6


Trình bày cơ sở lý thuyết phương pháp điều khiển trượt.
Chương 2. Thiết kế bộ điều khiển trượt và bộ quan sát trượt
Trình bày phương pháp thiết kế bộ điều khiển trượt và bộ quan sát trượt.
Chương 3. Ứng dụng điều khiển trượt vào điều khiển robot planar hai bậc
tự do
Thiết kế bộ điều khiển trượt và bộ quan sát trượt cho robot planar. Trên cơ sở
đó xây dựng hệ thống điều khiển kết hợp với bộ quan sát trượt cho robot. Cuối cùng
tiến hành mô phỏng và đánh giá kết quả đạt được.
Trong quá trình nghiên cứu, tác giả luận văn đã cố gắng tiếp cận và giải
quyết vấn đề một cách triệt để nhất. Tuy vậy, do thời gian có hạn và trình độ chun
mơn cịn nhiều điểm chưa hồn thiện, chắc chắn sẽ khơng tránh khỏi những sai sót
nhất định. Kính mong nhận được sự đóng góp và chỉ bảo thêm của các thầy cô.
Xin trân trọng gửi lời cảm ơn tới Viện Đào tạo Sau đại học, Bộ môn Điều
khiển Tự động trường Đại học Bách Khoa Hà Nội đã tạo mọi điều kiện thuận lợi
cho tác giả trong quá trình thực hiện luận văn.
Xin được bày tỏ lòng biết ơn sâu sắc tới PGS.TS. Phan Xuân Minh, người đã
định hướng và tận tình chỉ bảo, giúp đỡ để tác giả có thể hồn thành luận văn tốt
nghiệp.
Cuối cùng, xin được gửi lời cảm ơn sâu sắc tới gia đình, bạn bè và các đồng
nghiệp, những người ln ủng hộ nhiệt tình và là nguồn động viên to lớn đối với tác
giả trong suốt quá trình nghiên cứu và hoàn thành luận văn.
Hà nội, ngày 20 tháng 09 năm 2012

Học viên

Nguyễn Thị Ngọc Xuân

7


CHƯƠNG 1. PHƯƠNG PHÁP ĐIỀU KHIỂN TRƯỢT
1.1. Vài nét về lịch sử điều khiển trượt
Những lợi ích của điều khiển trượt đã được chứng minh từ lâu. Trong số đó
có sự đơn giản khi thiết kế và điều khiển chuyển động độc lập (miễn là các điều
kiện trượt được duy trì), bất biến với các thay đổi của quá trình và nhiễu loạn bên
ngoài, với rất nhiều chế độ làm việc ví dụ như là điều chỉnh, điều khiển bám theo
quỹ đạo, điều khiển theo mơ hình và bộ quan sát. Chính vì ý nghĩa ứng dụng mà
điều khiển trượt được nghiên cứu và phát triển không ngừng. Mặc dù đã có rất
nhiều cơng trình được cơng bố theo hướng này, nhưng SMC vẫn luôn là đối tượng
của nhiều nghiên cứu (lý thuyết và liên quan đến nhiều úng dụng khác nhau).
SMC về cơ bản là một hệ quả của điều khiển không liên tục. Đầu những năm
sáu mươi, điều khiển không liên lục (trường hợp đơn giản nhất là điều khiển bang bang) là một đề tài nghiên cứu của các kỹ sư điều khiển và cơ khí. Ví dụ như nghiên
cứu của Hamel ở Pháp , hoặc Cypkin và Emelyanov ở Liên Xô đã giải quyết một
cách chặt chẽ vấn đề các dao động xuất hiện trong các hệ thống điều khiển bang –
bang. Những nghiên cứu đầu tiên quan tâm đến việc làm thế nào để nhanh chóng
tổng hợp các vấn đề bằng nhiều phương pháp khác nhau hơn là quan tâm đến việc
phân tích các hiện tượng phiền hà xuất hiện trong hệ thống để tránh. Một trong
những phương pháp đó là SMC và bài tốn điều khiển tối ưu tác động nhanh.
Trong thực tế, khi đi tìm kiếm các phương pháp thiết kế mà bây giờ chúng ta
gọi điều khiển bền vững thì chế độ trượt chính là sự khám phá đầu tiên, xuất hiện ở
những năm sáu mươi. Thậm chí trước khi khái niệm “ điều khiển bền vững” được
sử dụng thì đã có các giải thuật điều khiển đảm bảo hệ thống điều khiển không nhạy
cảm với những sự thay đổi của đối tượng và của nhiễu. Các bộ điều khiển tuyến

tính thường chỉ đảm bảo chất lượng của hệ thống điều khiển khi đối tượng thay đổi
trong phạm vi nhỏ và các nhiễu tác động vào hệ thống là hằng số hoặc nhiễu biến
đổi chậm.

8


Vào đầu năm 1962, dựa vào ý tưởng của B. Hamel, những nghiên cứu bù phi
tuyến đã được khởi xướng, mục đích của những nghiên cứu này là khắc phục những
hạn chế trước đó. Thơng thường, những hệ thống này hoạt động dựa vào tín hiệu sai
lệch của hệ thống phản hồi, được xác định bởi mối quan hệ sau:
u = F1 ( x, x ' ,...) sgn( F2 ( x, x ' ,...))

Trong đó

(1.1)

là ký hiệu trị số tuyệt đối, F1 và F2 là các hàm tuyến tính. Do đó

tín hiệu điều khiển u của hệ thống là khơng liên tục và là một hàm của x và các đạo
hàm của nó. Một ví dụ đơn giản nhất thay thế bộ điều chỉnh PD cổ điển là:
u = − x sgn( x + kx ' )

(1.2)

1.2. Cơ sở lý thuyết điều khiển trượt [3]
1.2.1.Điều khiển đối tượng tích phân kép
1.2.1.1.Điều khiển phản hồi trạng thái
Bộ điều khiển u = r (e ) đưa vector trạng thái x = (x1 , x 2 ) T của đối tượng tuyến
tính, tích phân kép có mơ hình trạng thái :

0 
d x 0 1 
=
x +  u

dt 0 0
1

, y = x1

với u ≤ 1 , về được vị trí mong muốn x m .
Vector trạng thái mẫu x m có thể là vector hằng nếu trạng thái đích mong
muốn đã được xác dịnh cụ thể, song cũng có thể là 1 vector hàm theo thời gian nếu
bài tốn có nhiêm vụ tổng quát hơn là đưa trạng thái x(t ) của hệ bám theo một quỹ
đạo mẫu x m (t ) mong muốn nào đó.

9


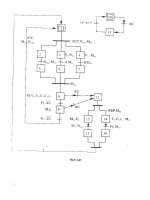
Hình 1.1. Thiết kế bộ điều khiển trượt cho đối tượng tích phân kép
Để đạt được mục đích đề ra là x(t ) → x m (t ) thì bộ điều khiển u = r (e ) cần
phải tạo ra được e(t ) → 0 . Ngoài ra, do giữa 2 phần tử x1 (t ) và x 2 (t ) của vector
trạng thái x(t ) có quan hệ

dx 2
= x 2 nên giữa 2 phần tử của vector tín hiệu chủ đạo
dt

x 
dx m1

= x m 2 và điều này kéo theo
x m =  m1  cũng phải có quan hệ tương ứng là
dt
 xm 2 

quan hệ phải có

de1
= e2 giữa 2 phần tử e1 (t ) và e2 (t ) của vector sai lệch trạng
dt

thái.
Xét hàm :
s (e ) = ke1 + e2 = ke1 +

de1
dt

với k > 0

Ta thấy do có k > 0 nên phương trình vi phân s(e ) = 0 có đa thức đặc tính:
A(s) = k + s
là đa thức Hurwitz. Do đó nghiệm e1 (t ) cũng như e(t ) của nó ln tiến về 0
(nghiệm ổn định). Bởi vậy, cuối cùng bộ điều khiển u = r (e ) cũng chỉ cần làm cho
s (e ) → 0 là đủ.

Hiển nhiển rằng để làm được điều này, bộ diều khiển phải tạo ra được dấu
của hàm s(e ) luôn ngược với dấu đạo hàm của nó là
0 thì phải tạo ra được


ds (e )
, nói cách khác khi s(e ) >
dt

ds
< 0 để làm giảm giá trị của nó, ngược lại khi s (e ) < 0 thì
dt

phải tăng giá trị nó lên bằng cách tạo ra

ds
> 0 hay :
dt

10


ds
sgn (s ) < 0
dt

⇔

 de1 de2 
+
k
 sgn (ke1 + ke2 ) < 0
dt 
 dt


(1.3)

Bất phương trình (1.3) chính là điều kiện để thiết kế bộ điều khiển trượt
u = r (e ) sao cho trạng thái x(t ) của hệ thống bám được theo quỹ đạo mẫu x m (t ) .

Từ (1.3) ta có thể dễ dàng có được các bộ điều khiển khác nhau. Chẳng hạn
như:
 de  dx
dx 
 de1 de2 
+
k
 sgn (s ) < 0 ⇔ k 1 +  m 2 − 2  sgn (s ) < 0
dt 
dt 
 dt
 dt  dt
 de  dx

⇔ k 1 +  m 2 − u  sgn (s ) < 0

 dt  dt
⇔k

< 0
de1 dx m 2
+
−u = 
dt
dt

> 0

khi s (e ) > 0
khi s (e ) < 0

  de1 dx m 2 
>  k dt + dt 
 

⇔ u = r (e ) = 
 <  k de1 + dx m 2 
  dt
dt 

khi s(e ) > 0
khi s (e ) < 0

(1.4)

Và nếu như không bị ràng buộc bởi điều kiện u ≤ 1 thì từ (1.4) ta cịn có:
 de dx 
u = r [e] =  k 1 + m 2  + λ sgn (s (e ))
dt 
 dt

với ∀ λ > 0

(1.5)

1.2.1.2. Vector tin hiệu mẫu là hằng số

Khi vector tin hiệu mẫu x m (t ) có dạng hằng số thì khơng mất tính tổng quát
0 

ta có thể giả sử đó là gốc tọa độ x m =  
0 
Từ điều kiện (1.3) ta có:
 dx1 dx 2 
+
k
 sgn (ke1 + e2 ) > 0
dt 
 dt

11


⇔ (kx 2 + u )sgn (ke1 + e2 ) > 0

(1.6)

⇔ kx 2 sgn (ke1 + e2 ) + u sgn (ke1 + e2 ) > 0

Và nếu kết hợp với điều kiện u ≤ 1 ta có thể chọn u như sau:
− 1
u = r (e ) = sgn (ke1 + e2 ) = 
 1

khi
khi


s(e ) < 0

s(e ) > 0

(1.7)

Ngồi ra từ mơ hình trạng thái của đối tượng và với một giá trị u cố định

(u = ±1) ,

x1 có quan hệ với x 2 xác định theo phương pháp tách biến như sau :
dx1 x 2
x2
=
⇒ u = 2 +c
dx 2
u
2u

(1.8)

Trong đó c là hằng số phụ thuộc vào giá trị ban đầu của x1 và x 2 .
Từ phương trình (1.8) và với quan hệ x1 = −e1 , x 2 = −e2 ta được :
e22
e1 = −
−c
2u

a)


b)

Hình 1.2. Quỹ đạo sai lệch trạng thái và hiện tượng trượt về gốc tọa độ
Quỹ đạo sai lệch trạng thái của hệ là sự ghép nối của các đoạn parabol rời nét
và liền nét mỗi khi nó đi qua đường ranh giới phân chia miền giá trị ± 1 của u là
s (e ) = 0 . Khi quỹ đạo trạng thái đi vào đoạn P1 P2 giữa 2 điểm tiếp xúc của đường

trượt với các parabol thì nó sẽ trượt dọc theo đường trượt về gốc tọa độ (hình 1.2b).

12


Hiện tượng trượt về gốc tọa độ còn được gọi là hiện tượng bang-bang hay
chattering. Độ dốc k của đường trượt được xác định độ dài P1 P2 . Độ dốc k càng lớn,
khoảng trượt P1 P2 càng nhỏ.
Rõ ràng quỹ đạo sai lệch trạng thái ln có xu hướng tiến về gốc tọa độ và
kết thúc tại đó. Điều này chỉ rằng hệ ổn định tiệm cận tại 0 với miền ổn định là tồn
bộ khơng gian trạng thái (ổn định tuyệt đối).
1.2.1.3. Điều khiển phản hồi tín hiệu ra
Để ý tiếp quan hệ giữa tín hiệu ra y (t ) với 2 trạng thái x1 (t ) và x 2 (t ) của
khâu tuyến tính, tích phân kép :
y = x1 ;

de
dy dx1
=
= x 2 ; e2 = 1
dt
dt
dt


Tức là hệ điều khiển trượt đối tượng tích phân kép theo nguyên tắc phản hồi
tín hiệu ra với cấu trúc hình 1.3 sẽ có bộ điều khiển là :
de 

u = r (e ) = sgn  ke + 
dt3
1424
s (e )

Trong đó: e1 = e, hay e = ω − y

Hình 1.3. Điều khiển trượt đối theo nguyên tắc phản hồi tín hiệu ra
Để điều khiển trạng thái x(t ) của hệ thống bám theo được vector tín hiệu chủ
đạo x m (t ) khi không bị ràng buộc bởi điều kiện u ≤ 1 , ta đã có bộ điều khiển (1.5)
làm việc theo nguyên tắc phản hồi trạng thái x(t ) như sau:

13


 de dx 
u =  k 1 + m 2  + λ sgn (s (e ))
dt 
 dt

với ∀ λ > 0

Nhằm chuyển bộ điều khiển trên cho việc điều khiển phản hồi tín hiệu ra, ta
sử dụng các mối quan hệ :
ω = x m1 ,


e=ω− y

de1 de
=
,
dt
dt

dx m 2 d 2 x m1 d 2ω
=
= 2
dt
dt 2
dt

Tức là
và

s (e ) = ke +

de
dt

Thì sẽ đi đến hình 1.4
 de d 2ω 
de 

u =  k
+ 2  + λ sgn  ke + 

dt 

 dt dt 

, λ>0

Hình 1.4. Điều khiển trượt bám đối tượng tích phân kép
1.2.2. Nguyên tắc chung của điều khiển trượt
Sau phần tìm hiểu nguyên lý điều khiển trượt cho đối tượng tích phân kép ta
có thể tổng kết lại và rút ra được ba điểm cơ bản về bài tốn thiết kế bộ điều khiển
trượt như sau:
1) Mục đích của điều khiển là tạo ra e(t ) → 0 với e(t ) là sai lệch giữa tín hiệu
chủ đạo ω (t ) và tín hiệu đầu ra y (t ) của hệ thống.

14


2) Để đạt được e(t ) → 0 , trong điều khiển trượt người ta sử dụng hàm trượt:
s (e) = a 0 e + a1

de
d n −2 e d n −1e
+ ......... + a n − 2 n − 2 + n−1
dt
dt
dt

(1.9)

Trong đó n là bậc của mơ hình đối tượng điều khiển và các hệ số

a 0 , a1 , ...., a n− 2 phải được chọn sao cho phương trình vi phân:
s (e ) = 0

(1.10)

có đa thức đặc tính
A( s ) = a 0 + a1 s + ....... + a n − 2 s n− 2 + s n −1

(1.11)

là đa thức Hurwitz. Điều này sẽ đảm bảo rằng không phụ thuộc vào các giá trị đầu,
nghiệm e(t ) của phương trình (1.10) ln ln thoả mãn được điều kiện e(t ) → 0 .
Phương trình (1.10) mơ tả mặt phẳng s(e) = 0 có tên gọi là mặt trượt (sliding
surface) trong không gian n chiều có các trục toạ độ e,

de d 2 e
d n − 2 e d n −1e
, 2 ,........., n− 2 , n −1 .
dt dt
dt
dt

3) Với hàm trượt s(e) , nhiệm vụ của bộ điều khiển nay được cụ thể rõ ràng hơn
là phải tạo ra được s(e) = 0 để có e(t ) → 0 và điều này tương đương với việc
phải tạo ra được:
s (e)

ds (e)
<0
dt


(1.12)

Điều kiện (1.12) được gọi là điều kiện trượt (sliding condition)
1.3. Đặc tính bền vững của điều khiển trượt [2]
1.3.1. Bộ điều khiển trượt ổn định bền vững
Một tính năng quan trọng của điều khiển trượt là bền vững với sự thay đổi
của các tham số động học của đối tượng điều khiển và bất biến đối với các tác động
nhiễu bên ngoài. Để làm rõ điều này chúng ta xét một đối tượng điều khiển có mơ
hình vào ra như sau:

15


dny
dy
d n −1 y
= f ( y, ,..., n −1 ) + u
dt
dt n
dt

(1.13)

Trong đó hàm phi tuyến f là bất định. Giả thiết rằng f
f

∞

∞


là hữu hạn, tức là:

≤δ <∞

(1.14)

Lần lượt đặt các biến trạng thái là x1 = y, x 2 =

dy
d n −1 y
,..., x n = n −1 ta sẽ có mơ
dt
dt

hình trạng thái của đối tượng là:
 dxi
 dt = xi +1 voi 1 ≤ i ≤ n − 1
 dx
n
= f ( x) + u

dt

 y = x1


(1.15)

Trong đó x = ( x1 , x 2 ,..., x n ) T . Nhiệm vụ điều khiển đặt ra ở đây là phải tìm ra

bộ điều khiển phản hồi tín hiệu ra y , để với nó và khi ω = 0 hệ kín ở hình 1.5 ln
có x(t ) → 0 .
ω

e

Bộ điều
khiển trượt

u

Đối tượng

y

-

Hình 1.5. Bộ điều khiển trượt ổn định bền vững
Gọi a 0 , a1 ,......, a n− 2 là bộ các hằng số được chọn sao cho đa thức đặc tính:
A( s ) = a 0 + a1 s + ....... + a n − 2 s n− 2 + s n −1

(1.16)

Là đa thức Hurwitz, khi đó ta có hàm trượt xác định theo (1.9) là:
s (e) = a 0 e + a1

de
d n −2 e d n −1e n−1 d i e
+ ......... + a n − 2 n − 2 + n−1 = ∑ ai i
dt

dt
dt
dt
0

16

(1.17)


Trong trường hợp phương trình vi phân s(e) = 0 có đa thức đặc tính A(s) là
đa thức Hurwitz thì nhiệm vụ của bộ điều khiển trượt sẽ được thay thế bằng nhiệm
vụ đơn giản hơn là:
s (e ) → 0 ⇔ s (e )

ds (e)
<0
dt

(1.18)

Tóm lại chúng ta phải thiết kế bộ điều khiển phản hồi tín hiệu ra y thoả mãn
điều kiện trượt (1.18).
Từ biểu thức mặt trượt (1.17) và mơ hình đối tượng điều khiển (1.15) ta có:
n−2
n−2
dx
ds (e) n −1 d i +1e
= ∑ ai i +1 = −∑ ai xi + 2 − n = −∑ ai xi + 2 − f ( x) − u
dt

dt
dt
i =0
i=0
i =0

Và từ điều kiện trượt (1.18) ta có:
n−2
> 0 khi s < 0
ds (e)
= −∑ ai xi + 2 − f ( x) − u = 
dt
i =0
< 0 khi s > 0

 n−2
< −∑ ai xi + 2 − f ( x) khi s < 0
⇔ u =  ni =−02
> −∑ ai xi + 2 − f ( x) khi s > 0
 i =0

(1.19)

Kết hợp với giả thiết (1.14) ta có bộ điều khiển trượt cần tìm là:
 n−2
< −∑ a i xi + 2 − δ
u =  ni =−02
> − ∑ a i x i + 2 + δ
 i =0


khi s < 0

(1.20)
khi s > 0

Ta thấy bộ điều khiển (1.20) hoàn tồn khơng phụ thuộc vào mơ hình của đối
tượng điều khiển nên nó chính là bộ điều khiển bền vững.
Ta có thể dễ dàng chứng minh được bộ điều khiển phản hồi đầu ra y thoả
mãn điều kiện (1.20) là:
u = (k + δ ) sgn( s ) với k > 0 tuỳ chọn

17

(1.21)


Thật vậy, ta xét bộ điều khiển phản hồi đầu ra (1.21) ứng với ω = 0 .
Trường hợp s > 0 : u = (k + δ ) kết hợp với mơ hình (1.15) và giả thiết (1.14)
ta được

dx n
> k . Điều này chứng tỏ rằng phải tồn tại T1 hữu hạn để có x n > 0 khi
dt

t > T1 .

Tiếp tục, do có

dx n−1
= x n > 0 khi t > T1 nên cũng phải tồn tại T2 để x n −1 > 0

dt

khi t > T1 + T2.
Cứ lý luận như vậy ta sẽ thấy phải tồn tại T = T1 + T2 + …..+ Tn hữu hạn để
đồng thời có xi > 0 , 1 ≤ i ≤ n khi t > T. Kết hợp thêm với tính chất Hurwitz của đa
thức đặc tính A(s) , tức là ai > 0, 0 ≤ i ≤ n − 2 thì khi t > T cũng sẽ có:
n−2

∑a x
i =0

i

n−2

i+ 2

> 0 ⇒ k + δ > −∑ ai xi + 2 + δ
i =0

Và do đó bộ điều khiển phản hồi đầu ra (1.21) thoả mãn điều kiện (1.20), ít
nhất là khi t > T.
Lý luận tương tự cho trường hợp s < 0 ta cũng thấy (1.21) sẽ thoả mãn (1.20)
khi t > T.
Vậy cả hai trường hợp s < 0 và s > 0 luôn tồn tại T hữu hạn sao cho khi có t
> T bộ điều khiển phản hồi đầu ra (1.21) sẽ thoả mãn điều kiện đủ (1.20) của điều
kiện trượt và do đó nó làm đối tượng (1.15) ổn định tiệm cận.
Nhận xét:
-


Bộ điều khiển trượt (1.21) chỉ có nhiệm vụ làm cho s(e) → 0 , nói cách khác
nó chỉ có nhiệm vụ đưa quỹ đạo trạng thái tự do x(t ) của hệ thống kín về tới
mặt trượt s(e) = 0 . Khi đã về tới mặt trượt, quỹ đạo trạng thái tự do x(t ) của
hệ kín sẽ tự trượt về gốc toạ độ.

18


-

Khi hằng số k của bộ điều khiển (1.21) được chọn càng lớn, thời gian T sẽ
càng nhỏ, và do đó tốc độ s(e) → 0 càng cao, hay quỹ đạo trạng thái tự do
x(t ) của hệ kín càng tiến nhanh về mặt trượt s (e) = 0 .

-

Khi đa thức đặc tính A(s) của phương trình vi phân s(e) = 0 có các nghiệm
s i nằm càng xa trục ảo về phía trái, quỹ đạo trạng thái tự do x(t ) của hệ kín

càng trượt nhanh trên mặt trượt về gốc toạ độ.
-

Các bộ điều khiển trượt mang tính bền vững rất cao song chúng lại có chung
một nhược điểm chính là tạo ra hiện tượng rung (chattering) trong hệ thống.

-

Trong trường hợp điều kiện ràng buộc (1.14) khơng được thoả mãn, song ta
lại tìm được một hàm µ ( x) nào đó là hàm chặn trên của f (x) theo nghĩa:
f ( x) ≤ µ ( x) , ∀ x


Thì ta lại vẫn có được bộ điều khiển GAS bền vững phản hồi trạng thái, đó là
những bộ điều khiển thoả mãn điều kiện đủ, được suy ra từ (1.19) như sau:
 n−2
< −∑ a i xi + 2 − µ ( x) khi s < 0
u =  ni =−02
> −∑ a i xi + 2 + µ ( x) khi s > 0
 i =0

Chẳng hạn như:
u = (k + µ (( x)) sgn( s ) với k > 0 tuỳ chọn

Hơn nữa, nếu hàm µ (x) chỉ phụ thuộc x1 = y thì bộ điều khiển trên trở thành
bộ điều khiển bền vững phản hồi đầu ra.
1.3.2. Bộ điều khiển trượt bám bền vững
Bây giờ nhiệm vụ đặt ra là bộ điều khiển phải làm cho tín hiệu ra y (t ) của hệ
bám theo được tín hiệu mẫu ω (t ) cho trước theo nghĩa (tracking control):
lim w(t ) − y (t ) = 0
t →∞

19


Xét đối tượng phi tuyến (1.15) thoả mãn điều kiện (1.14). Gọi ω (t ) là tín
hiệu mẫu, hàm s(e) định nghĩa bởi (1.17) là mặt trượt và phương trình vi phân
s (e) = 0 có đa thức đặc tính (1.16) là đa thức Hurwitz. Ta ký hiệu:

dw
d n − 2 w d n −1 w
q (t ) = a 0 w + a1

+ ......... + a n −2
+ n −1
dt
dt n −
dt

Nếu có q

∞

≤ σ với σ là số dương hữu hạn, thì đối tượng (1.15) sẽ được

điều khiển bám bền vững bằng bộ điều khiển phản hồi đầu ra:
u = (k + δ + σ ) sgn( s ) với k > 0 tuỳ ý chọn

(1.22)

Để chứng minh chúng ta làm tương tự phần 1.3.1. nhưng ở đây ta có
e = ω − y nên điều kiện (1.20) được thay bằng điều kiện sau:

 n−2
< −∑ a i xi + 2 − q (t ) − δ
u =  ni =−02
> −∑ a i xi + 2 − q (t ) + δ
 i =0

Và q

∞


khi s < 0
khi s > 0

≤ σ nên các bộ điều khiển thoả mãn điều kiện đủ trên sẽ là:
 n−2
< −∑ a i xi + 2 − σ − δ
u =  ni =−02
> − ∑ a i x i + 2 − σ + δ
 i =0

khi s < 0

(1.23)
khi s > 0

Trong trường hợp ta chỉ quan tâm tới chất lượng bám theo tín hiệu mẫu ω (t )
của tín hiệu ra y (t ) sau một khoảng thời gian hữu hạn T đủ nhỏ thì rõ ràng bộ điều
khiển phản hồi đầu ra (1.22) là thoả mãn điều kiện đủ (1.23) khi t > T. Hằng số k
trong (1.22) được chọn càng lớn, khoảng thời gian T càng nhỏ và do đó chất lượng
bám sẽ càng cao.
1.4. Hiện tượng rung (chattering) trong điều khiển trượt
Một chế độ trượt lý tưởng khơng tồn tại trong thực tế vì điều đó có nghĩa là
hệ thống điều khiển sẽ làm việc với tần số chuyển đổi vô cùng lớn ( ∞ ). Những

20


khiếm khuyết của quá trình chuyển đổi như thời gian trễ trong q trình chuyển đổi,
đặc điểm qn tính của các cơ cấu chấp hành, sự không liên tục trong điều khiển
phản hồi tạo ra đặc tính động học đặc biệt trong vùng lân cận của mặt trượt và

thường được gọi là hiện tượng rung (chattering) như hình 1.8.

Hình 1.6. Hiện tượng chattering
Nhược điểm của hiện tượng này là ngay cả khi đầu ra của hệ thống đã được
lọc thì nó vẫn có thể kích thích các chế độ tần số cao làm giảm hiệu suất của hệ
thống và thậm chí có thể dẫn đến mất ổn định. Hiện tượng chattering cũng làm cho
bộ phận chuyển động cơ khí bị hao mịn nhanh chóng và dẫn đến sự thất thốt nhiệt
lớn trong các mạch điện. Đó là lý do vì sao có rất nhiều cơng trình nghiên cứu được
thực hiện để làm giảm hoặc loại bỏ hiện tượng chattering này. Sau đây xin giới
thiệu một số phương pháp cụ thể như sau.
1.4.1. Phương pháp lớp biên để làm giảm hiện tượng chattering
Đây là phương pháp đơn giản nhất để khắc phục hiện tượng chattering, được
thực hiện bằng cách thay thế khâu relay hai trạng thái sgn bằng khâu khuyếch đại
bão hồ sat như hình 1.7.

21


Hình 1.7. Hàm bão hồ sat(s)
Phương trình tốn học mơ tả khâu khuyếch đại bão hoà như sau:
 1 khi
s>Φ
s
sat ( s ) = 
khi − Φ ≤ s ≤ Φ
Φ
s < −Φ
− 1 khi

Tín hiệu điều khiển khơng liên tục được làm nhẵn trong một lớp biên mỏng

B(t):
B(t ) = {x : s ( x, t ) ≤ Φ}

(1.24)

Hình 1.8. Định nghĩa lớp biên B(t)
Lớp này bao quanh mặt trượt s(t ) = 0 với bề dày Φ và độ rộng ε.
Nếu luật điều khiển bảo đảm cho điều kiện trượt (1.12) được thỏa mãn ở bên
trong lớp biên B(t) thì sau một thời gian hữu hạn, sai số điều khiển sẽ bé hơn ε,
nghĩa là:
e(t ) ≤ ε

(1.25)

22


Khi s < Φ thì sat ( s) =

s
là hàm liên tục nên tín hiệu sẽ giảm chattering,
Φ

nhưng xảy ra sai lệch quỹ đạo.
1.4.2. Phương pháp dùng hàm chuyển mạch tích phân bão hồ sat-PI
Để vừa giảm hiện tượng chattering, vừa giảm sai lệch quỹ đạo ta thay thế
hàm sat bằng một hàm chuyển mạch tích phân-bão hịa (sat-PI) như sau:

sgn( s )


t
σ ( s) =  s
+ K I ∫ s (τ ) ⋅ dτ
Φ
to


khi

s >Φ

khi − Φ ≤ s ≤ Φ

(1.26)

trong đó KI là hệ số tích phân dương, to là thời điểm đầu khi trạng thái hệ
thống đi vào trong lớp biên B(t).
Giả sử rằng hệ số tích phân KI được chọn đủ lớn sao cho:
.
 s + K I s > 0 khi s > 0
 Φ

 .
 s + K s < 0 khi s < 0
I
 Φ

(1.27)

Chúng ta chứng minh được rằng với luật điều khiển u được xây dựng với

hàm chuyển mạch σ(s) được định nghĩa theo (1.26) và nếu ta chọn các hệ số KI theo
(1.27) thì điều kiện trượt được thỏa mãn và sai số quỹ đạo sẽ hội tụ tiệm cận về 0.
Việc sử dụng hàm sat – PI đảm bảo loại bỏ được hiện tượng chattering đồng
thời giảm được sai số quỹ đạo so với khi sử dụng hàm sat. Thuật tốn đưa ra có khả
năng điều khiển hệ phi tuyến bậc cao, hệ điều khiển làm việc ổn định, ít chịu ảnh
hưởng của tải, do đó chất lượng điều khiển được cải thiện đáng kể.
1.5. Kết luận

23


SMC là phương pháp điều khiển tiếp cận mạnh mẽ để điều khiển các hệ
thống phi tuyến và bất định. Khi hoạt động ở chế độ trượt, hệ thống có các ưu điểm
nổi bật sau đây:
1) Đảm bảo tính bền vững: khi hoạt động ở chế độ trượt, sự thay đổi của các
tham số động học của đối tượng điều khiển trong phạm vi nhất định sẽ không
làm thay đổi chất lượng của hệ thống. Sở dĩ như vậy là do điều kiện trượt
được thể hiện ở dạng các bất đẳng thức. Sự thay đổi các tham số động học
trong phạm vi cho phép của các bất đẳng thức sẽ không làm mất đi chế độ
trượt của hệ thống.
2) Đảm bảo tính bất biến đối với các tác động nhiễu loạn bên ngoài: nếu trong
hệ thống điều khiển với cấu trúc biến đổi đảm bảo được điều kiện cần và đủ
cho chế độ trượt thì hệ thống sẽ hoạt động với chất lượng không thay đổi,
không phụ thuộc vào các tác động bên ngoài mà chỉ phụ thuộc vào mặt trượt.
Đây chính là khả năng bất biến của hệ thống làm việc ở chế độ trượt.
Như vậy, SMC là phương pháp điều khiển bền vững có thể áp dụng cho hệ
bất định. Tuy vậy phương pháp này còn bộc lộ khuyết điểm chính là hoạt động điều
khiển khơng liên tục, là nguyên nhân gây ra hiện tượng rung (hiện tượng
chattering). Do đó các nhà khoa học đã nghiên cứu và tìm ra nhiều phương pháp để
loại bỏ hiện tượng này, ví dụ như phương pháp lớp biên dùng hàm bão hồ sat,

phương pháp dùng hàm chuyển mạch tích phân bão hoà sat – PI.

24