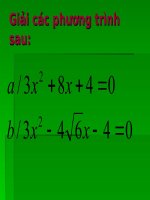Chuong IV 5 Cong thuc nghiem thu gon

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (843.42 KB, 14 trang )

KIỂM TRA BÀI CŨ
Câu 1: Viết công thức nghiệm của phương trình bậc hai.
Câu 2: Giải phương trình: 5x 2 - 6x + 1 = 0

Câu 1: Cơng thức nghiệm của phương trình bậc hai

Đối với PT: ax2 + bx + c = 0 (a ≠ 0)

∆ = b2 – 4ac
Nếu ∆ > 0 thì phương trình có 2 nghiệm phân biệt:
b 
b 
x1 
; x2 

2a
2a
b
Nếu ∆ = 0 thì phương trình có nghiệm kép: x1  x2 

2a

Nếu ∆ < 0 thì phương trình vơ nghiệm

Câu 2: Giải phương trình:
Ta có:

5x 2 - 6x + 1 = 0

 a = 5; b = -6; c = 1

Δ = b 2 - 4ac = (-6)2 - 4.5.1 = 16 > 0
Δ = 16 = 4

Vậy phương trình có hai nghiệm phân biệt:

-b +  6 + 4 1
x1 =
=
=
2a
2.5
2

-b -  6 - 4 1
x2 =
=
=
2a
2.5 5

Tiết 55 : CƠNG THỨC NGHIỆM THU GỌN

1. Cơng thức nghiệm thu gọn:

Cho phương trình: ax2 + bx + c = 0
Đặt b = 2b’ :
Thì Δ = b2 – 4ac = (2b’)2 – 4ac

= 4b’2 – 4ac
= 4(b’2 – ac)
Kí hiệu : Δ’ = b’2 – ac
Ta có :
Δ = 4Δ’

(a ≠ 0)

?1

Từ bảng kết luận của bài trước hãy dùng các đẳng thức b = 2b’ và Δ = 4Δ’
để suy ra kết luận bằng cách điền vào chỗ trống

Đối với PT: ax2 + bx + c = 0 (a ≠ 0), và b = 2b’; ’ = b’2 - ac

( = 4 ’ ):

• Nếu  > 0 => ’ >…
0 thì phương trình có …………………….:
có 2 nghiệm phân biệt:
2   b '  '   b '  '
b 
 2b ' 4 '  2b ' 2  '



x1 
=…………….................................


a
2a
2a
2a
2a

b 
x2 
2a



 2b ' 4 '  2b ' 2  ' 2  b '  '



=…………….................................
2a
2a
2a



 b '  '

a

• Nếu  = 0 => ’ == 0…. thì phương trình có ……………
nghiệm kép :

b  2b '  b '
=…………….................................
x1  x2 
2a
a
2a

• Nếu  < 0 => ’ ………
<0
thì phương trình ……………..
vơ nghiệm.

* Cơng thức nghiệm thu gọn của phương trình bậc hai
Đối với phương trình ax2 + bx +c = 0 (a ≠ 0) và b = 2b’;
’ = b’2 - ac ( = 4 ’ ):
• Nếu ’ > 0 thì phương trình có 2 nghiệm phân biệt:

 b '  '
x1 
a

 b '  '
x2 
a

• Nếu ’ = 0 thì phương trình có nghiệm kép :
• Nếu ’ < 0 thì phương trình vơ nghiệm .

b'

x1 x2 
a

Để giải phương trình bậc
hai theo cơng thức nghiệm
thu gọn ta cần thực hiện
qua các bước nào?

?
=> Các bước giải một phương trình bậc hai theo cơng thức nghiệm thu gọn:
Bước 1: Xác định các hệ số a, b’, c.
Bước 2: Tính ’ = b’2 – ac rồi so sánh kết quả ’ với 0.
Bước 3: Kết luận số nghiệm, tìm nghiệm của phương trình.

So sánh công thức tổng quát với công thức thu gọn

Cơng thức nghiệm (tổng qt)
của phương trình bậc hai

Đối với PT: ax2 + bx + c = 0
(a ≠ 0), ∆ = b2 – 4ac

Công thức nghiệm thu gọn của
phương trình bậc hai

Đối với PT: ax2 + bx + c = 0
(a ≠ 0) và b = 2b’, ∆’ = b’2 – ac:

 Nếu ∆ > 0 thì phương trình có  Nếu ∆’ > 0 thì phương trình
có 2 nghiệm phân biệt:
2 nghiệm phân biệt:
b 
b 
x1 
; x2 
 x1   b '  ' ; x2   b '  ' 
2a
2a
a
a
 Nếu ∆ = 0 thì phương trình có  Nếu ∆’ = 0 thì phương trình
b có nghiệm kép:
b'
nghiệm kép:
x  x 
x  x 
1

2

2a

 Nếu ∆< 0 thì pt vơ nghiệm.

1

2

a

Nếu ∆’< 0 thì pt vơ nghiệm.

2. Áp dụng:
?2

Giải phương trình 5x2 + 4x – 1 = 0 bằng cách điền
vào những chỗ trống:

b’ = . .2 . . ;

a = . .5 . . ;

∆’ = .2.2 .–. 5.(-1)
.....=4+5=9>0

c = .–.1. .
∆’ = . 3. . .



Phương trình đã cho có hai nghiệm phân biệt:

x1 = . . –. 2. + 3 = 1 ;
5

5

x2 = –. 2. .–.3 = – 1
5

Bài tập : Trong các phương trình sau, phương
trình nào nên áp dụng công thức nghiệm thu gọn
để giải :
2

a ) 2 x  3 x  5 0
2

b) x  2 2 x  7 0
2

c ) x  2 x  2 0
Chó ý: Nếu hệ số b là số chẵn, hay bội chẵn ta nên dùng
công thức nghiệm thu gọn để giải phương trình bậc 2.

?3

Xác định a, b’, c rồi dùng công thức
nghiệm thu gọn giải các phương trình:
( Cá nhân 3’)

a) 3x2 + 8x + 4 = 0

b ) 7 x2 - 6 2 x + 2 = 0
( a 7; b /  3 2; c 2)

(a = 3; b’ = 4 ; c = 4)
2
'
Ta có:    3 2  7.2
Ta có: Δ’ = 42 - 3.4
= 16 – 12
= 18-14 = 4 >0
=4>0
Do Δ’ > 0 nên phương trình có Do Δ’ = 4 > 0 nên phương trình
có hai nghiệm phân biệt:
hai nghiệm phân biệt:





4 4
42
2
x1 


3
3
3

x1 =

-b' +Δ'

a

3 2+2
=
7

4 4
4 2
x2 

 2
3
3

x2 =

-b' -Δ'
a

3 2-2
=
7

Bài tập : giải phương trình sau
bằng cơng thức nghiệm thu gọn :
2
2

00

aa)) x 
22 22xx 7 7
2

22

bb)) x  22x x 2 
200

2  7 9  0

' ( 1) 2  1.(  2)
1  2 3  0

 3

 '  3

x1 

2  3;

x1 1  3;

x2 

2 3

x2 1 

' ( 2)  1.(  7)

3

HƯỚNG DẪN VỀ NHÀ
-Học thuộc công thức nghiệm thu gọn.
- BTVN : 17, 18, 19 SGK/ 49
- Soạn trước các bài 20-> 24 cho tiết
sau Luyện tập.

Chuong IV 5 Cong thuc nghiem thu gon

Tài liệu liên quan

Tài liệu bạn tìm kiếm đã sẵn sàng tải về