Gui em Kha Vi bai hinh 9 26
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (93.9 KB, 2 trang )
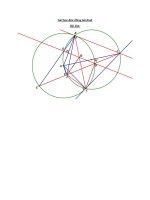
<span class='text_page_counter'>(1)</span>Nhờ Thầy Nguyễn Minh Sang giải bài Hình 9-26. Cảm ơn Thầy rất nhiều. Cho tam giác ABC nhọn (AB<AC) có đường cao AD (D thuộc BC) nội tiếp đường tròn (O). Vẽ DH vuông góc AB tại H, DK vuông góc AC tại K. a/.CM: Các tứ giác AHDK, BHKC nội tiếp. b/.HK cắt 2 đường thẳng AD,AO lần lượt tại E,F. CM: Góc AFK bằng 900 AB2 KE.KF 2 HE.HF c/.CM: AC d/.Trên 2 đoạn AB,AC lần lượt lấy 2 điểm M,N sao cho góc MDB bằng góc NDC. NB cắt AD tại I. CM: 3 điểm C,I,M thẳng hàng. c) Ta có tam giác FAK đ d tam giác DAB (g.g) suy ra FA FK AK BD. AK AB AD BD AB FK FA FH AH CD. AH AC AD CD AC FH. và tam giác FAH đ d tam giác DAC suy ra. FK 2 2 HE 2 S AHE AH . AE .sin HAE AK AH . FK AH HE .HF EK 2 S AEK AE . AK .SinEAK AK . HF AK 2 HF AK 2 KE .KF AH 2 2 2 2 AB AK . BD . FH HE. HF BD 2 . FH 2 . AC 2 AH 2 .CD 2 . FK 2 KE. KF CD 2 . FK 2 FK FH BD 2 FK 2 BD 2 .FH 2 Taco 1 BD CD CD 2 FH 2 CD 2 .FK 2 AH .. và. AB2 KE.KF 2 Vậy AC HE.HF d) . Qua A, kẻ đường thẳng song song với BC cắt DM, DN tại Q, P. Vì QP//BC nên DQP MDB ; NDC DPQ.
<span class='text_page_counter'>(2)</span> Mà NDC MDB Nên DQP DPQ Hay tam giác DQP cân tại D, mà DA vuông góc với BC,và QP//BC nên DA vuông góc với QP, Vậy DA là đường cao và là đường trung tuyến của tam giác DQP. Nên A là trung điểm của QP => AQ= AP AM AQ NC DC AP Vì QP//BC nên MB BD và A N A M BD NC A Q BD DC A Q . . . . 1 BD DC A P A P Xét MB DC A N ( vì AQ= AP) Nên các đường thẳng AD, BN, CM đồng quy tại 1 điểm là I Hay C, I , M thẳng hàng. ( Phần d cũng như bài của bạn Nguyễn Minh Nhật).
<span class='text_page_counter'>(3)</span>