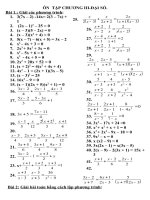BAI TAP CHUONG I DAI SO 8

<span class='text_page_counter'>(1)</span>CHƯƠNG I: PHÉP NHÂN VÀ PHÉP CHIA CÁC ĐA THỨC I. NHÂN ĐƠN THỨC VỚI ĐA THỨC – NHÂN ĐA THỨC VỚI ĐA THỨC Bài 1. Thực hiện các phép tính sau: 2 2 a) ( x –1)( x  2 x ). b) (2 x  1)(3x  2)(3 – x ). ( x  1)( x 2 – x  1) d) Bài 2. Thực hiện các phép tính sau:. 2 c) ( x  3)( x  3 x – 5). 3 e) (2 x  3 x  1).(5 x  2). 2 f) ( x  2 x  3).( x  4). 2 xy( x 2 y – 5 x  10 y )  2 x y (2 x – 3 y  5 yz ) ( x – 2 y )( x y  xy  2 y ) a) b) c) 5 1  3 2 2 x y.(3 xy – x 2  y)  xy –1 .( x – 2 x – 6) 2 2  d) 3 e) ( x – y )( x  xy  y ) f)  2 Bài 3. Chứng minh các đẳng thức sau: 3. 2. 2 2. 4 3 2 2 3 4 5 5 a) ( x  y )( x  x y  x y  xy  y ) x  y 4 3 2 2 3 4 5 5 b) ( x  y )( x  x y  x y  xy  y ) x  y 3 2 2 3 4 4 c) (a  b)(a  a b  ab  b ) a  b 2 2 3 3 d) (a  b)(a  ab  b ) a  b Bài 4. Thực hiện các phép tính, sau đó tính giá trị biểu thức: 4 3 2 a) A ( x  2)( x  2 x  4 x  8 x  16). với x 3 .. 7 6 5 4 3 2 b) B ( x  1)( x  x  x  x  x  x  x  1) 6 5 4 3 2 c) C ( x  1)( x  x  x  x  x  x  1). ĐS: A 211. với x 2 .. ĐS: B 255. với x 2 .. ĐS: C 129. 2 2 d) D 2 x (10 x  5x  2)  5 x (4 x  2 x  1) với x  5 . Bài 5. Thực hiện các phép tính, sau đó tính giá trị biểu thức: 1 x 2, y  3 2 2 3 A  ( x  x y  xy  y )( x  y ) 2. a) với 4. 3. 2 2. 3. 4. b) B (a  b)(a  a b  a b  ab  b ) 2. 2. 2. 2. 3. ĐS: D  5. ĐS:. với a 3, b  2 . 2 2. 3. x . c) C ( x  2 xy  2 y )( x  y )  2 x y  3x y  2 xy với Bài 6. Chứng minh rằng các biểu thức sau không phụ thuộc vào x: a) A (3x  7)(2 x  3)  (3x  5)(2 x  11). 1 1 , y  2 2.. A. 255 16. ĐS: B 275 3 C 16 ĐS:. 2 2 3 2 b) B ( x  2)( x  x  1)  x ( x  x  3x  2) 3 2 2 2 c) C  x ( x  x  3 x  2)  ( x  2)( x  x  1) 2 3 d) D  x (2 x  1)  x ( x  2)  x  x  3 2 2 e) E ( x  1)( x  x  1)  ( x  1)( x  x  1) Bài 7. * Tính giá trị của đa thức: 7 6 5 4 a) P( x ) x  80 x  80 x  80 x  ...  80 x  15. với x 79. ĐS: P(79) 94. 14 13 12 11 2 b) Q( x ) x  10 x  10 x  10 x  ...  10 x  10 x  10 với x 9. ĐS: Q(9) 1. 4 3 2 c) R( x )  x  17 x  17 x  17 x  20 với x 16. ĐS: R(16) 4. 10 9 8 7 2 d) S( x )  x  13x  13x  13x  ...  13x  13 x  10. với x 12. ĐS: S(12)  2.

<span class='text_page_counter'>(2)</span> II. HẰNG ĐẲNG THỨC Bài 1. Điền vào chỗ trống cho thích hợp: 2 a) x  4 x  4 ........... 2 b) x  8x 16  ........... c) ( x  5)( x  5)  ............ 2 x 3  12 x 2  48x  64  ...... e) x 3  6 x 2  12 x  8  ...... f) ( x  2)( x  2 x  4)  ....... d). 2 g) ( x  3)( x  3 x  9)  ........ 2 h) x  2 x  1  ....... 2 i) x –1  ....... 2 k) x  6 x  9  ........ 2 l) 4 x – 9  ........ 2 m) 16 x – 8x  1  ....... 2 o) 36 x  36 x  9  ......... 3 p) x  27  ..... 2 b) (5 x – y ) 2 1  x    4 e) . 2 3 c) (2 x  y ) 3 2 2 1  x  y   2  f)  3. 2 n) 9 x  6 x  1  ....... Bài 2. Thực hiện phép tính: 2 a) (2 x  3 y).  2 2 x  5 d)  g). 2    y  . x2  y  5   . (3 x 2 – 2 y )3. 2 2 2 4 2 h) ( x  3y )( x  3xy  9 y ) i) ( x  3).( x  3 x  9). 2 3 k) ( x  2 y  z)( x  2 y – z) l) (2 x –1)(4 x  2 x  1) m) (5  3 x ) Bài 3. Tính giá trị biểu thức bằng cách vận dụng hằng đẳng thức: 3 2 3 2 a) A  x  3 x  3 x  6 với x 19 b) B  x  3 x  3 x với x 11 ĐS: a) A 8005 b) B 1001 . Bài 4. Chứng minh các biểu thức sau không phụ thuộc vào x: 2 3 a) (2 x  3)(4 x  6 x  9)  2(4 x  1). 3 2 b) (4 x  1)  (4 x  3)(16 x  3). 3 3 2 2 c) 2( x  y )  3( x  y ) với x  y 1. 3 3 d) ( x  1)  ( x  1)  6( x  1)( x  1). ( x  5)2  ( x  5)2 x 2  25 e) ĐS: a) 29 b) 8 Bài 5. Giải các phương trình sau:. (2 x  5)2  (5 x  2)2 f) c) –1. x2 1 d) 8. 3 2 a) ( x  1)  (2  x )(4  2 x  x )  3x ( x  2) 17. e) 2. f) 29. 2 2 b) ( x  2)( x  2 x  4)  x ( x  2) 15. 3 2 2 2 c) ( x  3)  ( x  3)( x  3 x  9)  9( x  1) 15 d) x ( x  5)( x  5)  ( x  2)( x  2 x  4) 3 10 7 2 11 x x x x  9 2 15 25 ĐS: a) b) c) d) Bài 6. So sánh hai số bằng cách vận dụng hằng đẳng thức: 2 a) A 1999.2001 và B 2000 2 c) A 2011.2013 và B 2012 Bài 7. Tìm giá trị lớn nhất của biểu thức: 2 a) A 5 x – x. 2 4 8 16 b) A 2 và B (2  1)(2  1)(2  1)(2  1) 2 4 64 128 d) A 4(3  1)(3  1)...(3  1) và B 3  1. 2 b) B  x – x. 2 D –x 2  6 x  11 d) e) E 5  8 x  x Bài 8. Tìm giá trị nhỏ nhất của biểu thức:. 2 c) C 4 x – x  3 2 f) F 4 x  x  1. 2 a) A x – 6 x  11. 2 b) B  x – 20 x  101. d) D ( x  1)( x  2)( x  3)( x  6). 2 2 2 2 e) E  x  2 x  y  4 y  8 f) x  4 x  y  8y  6. 2 2 g) G  x – 4 xy  5 y  10 x – 22 y  28. 2 c) C x  6 x  11.

<span class='text_page_counter'>(3)</span> 2 2 HD: g) G ( x  2 y  5)  ( y  1)  2 2 Bài 9. Cho a  b S và ab P . Hãy biểu diễn theo S và P, các biểu thức sau đây: 2 2 a) A a  b. 3 3 b) B a  b. 4 4 c) C a  b. III. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ VẤN ĐỀ I. Phương pháp đặt nhân tử chung Bài 1. Phân tích các đa thức sau thành nhân tử: 4 3 2 4 b) 9 x y  3 x y. 2 a) 4 x  6 x. 3 2 c) x  2 x  5 x. 2 d) 3 x ( x  1)  5( x  1) e) 2 x ( x  1)  4( x  1) Bài 2. Phân tích các đa thức sau thành nhân tử:. f)  3 x  6 xy  9 xz. 2 2 a) 2 x y  4 xy  6 xy. 3 2 2 3 4 b) 4 x y  8 x y  2 x y. 2 3 4 2 3 2 4 c) 9 x y  3x y  6 x y  18xy 5 3 a3 x 2 y  a 3 x 4  a 4 x 2 y 2 2 e). 2 2 2 d) 7 x y  21xy z  7 xyz  14 xy. VẤN ĐỀ II. Phương pháp nhóm nhiều hạng tử Bài 1. Phân tích các đa thức sau thành nhân tử: 3 2 a) x  2 x  2 x  1 3. 2 b) x y  xy  x  1. 2 2 2 d) x  (a  b) x  ab e) x y  xy  x  y Bài 2. Phân tích các đa thức sau thành nhân tử: 2 a) ax  2 x  a  2a. 2 b) x  x  ax  a. 2. 3 2 d) 2 xy  ax  x  2ay e) x  ax  x  a Bài 3. Phân tích các đa thức sau thành nhân tử: 2 2 a) x  2 x  4 y  4 y. 4 3 b) x  2 x  4 x  4. c) ax  by  ay  bx 2 2 f) ax  ay  bx  by 2 c) 2 x  4ax  x  2a 2 2 3 2 f) x y  y  zx  yz 3 2 c) x  2 x y  x  2 y. 2 2 2 2 2 3 2 d) 3 x  3y  2( x  y ) e) x  4 x  9 x  36 f) x  y  2 x  2 y Bài 4. Phân tích các đa thức sau thành nhân tử: a) ( x  3)( x  1)  3( x  3) b) ( x  1)(2 x  1)  3( x  1)( x  2)(2 x  1) 2 c) (6 x  3)  (2 x  5)(2 x  1) d) ( x  5)  ( x  5)( x  5)  (5  x )(2 x  1) e) (3x  2)(4 x  3)  (2  3 x )( x  1)  2(3 x  2)( x  1). Bài 5. Phân tích các đa thức sau thành nhân tử: a) (a  b)(a  2b)  (b  a)(2a  b)  (a  b)(a  3b) c) ( x  y)(2 x  y)  (2 x  y)(3 x  y )  ( y  2 x ). 3 2 b) 5 xy  2 xyz  15y  6z 3 2 2 2 2 2 3 2 3 d) ab c  a b c  ab c  a bc. 2 2 2 e) x ( y  z)  y ( z  x )  z ( x  y). VẤN ĐỀ III. Phương pháp dùng hằng đẳng thức Bài 1. Phân tích các đa thức sau thành nhân tử: 2 a) 4 x  12 x  9. 2 b) 4 x  4 x  1. 2 c) 1  12 x  36 x. 2 2 d) 9 x  24 xy  16 y. x2  2 xy  4 y 2 e) 4. 2 f)  x  10 x  25.

<span class='text_page_counter'>(4)</span> 2 2 4 6 5 5 6 4 g)  16a b  24a b  9a b h) 25x  20 xy  4 y Bài 2. Phân tích các đa thức sau thành nhân tử:. 4 2 2 i) 25 x  10 x y  y. 2 a) (3x  1)  16. 2 2 b) (5x  4)  49 x. 2 2 c) (2 x  5)  ( x  9). 2 2 d) (3x  1)  4( x  2). 2 2 e) 9(2 x  3)  4( x  1). 2 2 2 2 2 2 f) 4b c  (b  c  a ). 2 2 g) (ax  by )  (ay  bx ). 2 2 2 2 h) (a  b  5)  4(ab  2). 2 2 2 2 i) (4 x  3 x  18)  (4 x  3 x ). 2 2 k) 9( x  y  1)  4(2 x  3y  1). 2 2 l)  4 x  12 xy  9 y  25 Bài 3. Phân tích các đa thức sau thành nhân tử:. 2 2 2 2 m) x  2 xy  y  4m  4mn  n. 6 3 b) 1  8 x y. 3 a) 8 x  64. 3 c) 125 x  1. y3 27 x  3 8 d) 8 x  27 e) Bài 4. Phân tích các đa thức sau thành nhân tử: 3. 3 3 f) 125 x  27 y. 3 2 3 2 2 3 a) x  6 x  12 x  8 b) x  3 x  3 x  1 c) 1  9 x  27 x  27 x 3 3 1 x3  x2  x  3 2 2 3 2 4 8 d) e) 27 x  54 x y  36 xy  8y Bài 5. Phân tích các đa thức sau thành nhân tử: 2 2 2 2 a) x  4 x y  y  2 xy. 6 6 b) x  y. 2 2 c) 25  a  2ab  b. 2 2 2 2 2 2 2 2 2 d) 4b c  (b  c  a ) e) (a  b  c)  (a  b  c)  4c Bài 6. Phân tích các đa thức sau thành nhân tử: 2 2 2 a) ( x  25)  ( x  5). 2 2 2 b) (4 x  25)  9(2 x  5). 2 2 2 c) 4(2 x  3)  9(4 x  9). 2 2 2 2 6 4 3 2 d) a  a  2a  2a e) (3 x  3x  2)  (3 x  3 x  2) Bài 7. Phân tích các đa thức sau thành nhân tử: 2 2 a) ( xy  1)  ( x  y ). 3 3 b) ( x  y )  ( x  y ). 2 2 2 d) 4( x  y )  8( x  ay)  4(a  1) Bài 8. Phân tích các đa thức sau thành nhân tử:. 4 2 3 2 2 2 c) 3 x y  3x y  3xy  3y. 3 e) ( x  y )  1  3xy( x  y  1) 3 2 3 c) x  3x  3 x  1  y. 3 2 a) x  1  5 x  5  3x  3. 5 4 3 2 b) a  a  a  a  a  1. 3 2 2 3 d) 5x  3x y  45xy  27 y. 2 2 e) 3x (a  b  c)  36 xy(a  b  c)  108y (a  b  c). VẤN ĐỀ IV. Một số phương pháp khác Bài 1. Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử) 2 a) x  5x  6. 2 b) 3 x  9 x  30. 2 c) x  3x  2. 2 d) x  9 x  18. 2 e) x  6 x  8. 2 f) x  5x  14. 2 2 2 g) x  6 x  5 h) x  7 x  12 i) x  7 x  10 Bài 2. Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử) 2 a) 3 x  5x  2. 2 b) 2 x  x  6. 2 c) 7 x  50 x  7. 2 d) 12 x  7 x  12. 2 e) 15 x  7 x  2. 2 f) a  5a  14. 2. 2 2 g) 2m  10m  8 h) 4 p  36 p  56 i) 2 x  5 x  2 Bài 3. Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử) 2 2 a) x  4 xy  21y. 2 2 b) 5 x  6 xy  y. 2 2 c) x  2 xy  15y.

<span class='text_page_counter'>(5)</span> 2 2 2 2 d) ( x  y )  4( x  y )  12 e) x  7 xy  10 y f) x yz  5 xyz  14 yz Bài 4. Phân tích các đa thức sau thành nhân tử: (tách một hạng tử thành nhiều hạng tử) 4 2 a) a  a  1. 4 2 b) a  a  2. 4 2 c) x  4 x  5. 3 3 3 2 d) x  19 x  30 e) x  7 x  6 f) x  5 x  14 x Bài 5. Phân tích các đa thức sau thành nhân tử: (thêm bớt cùng một hạng tử) 4 a) x  4. 4 b) x  64. 8 7 c) x  x  1. 8 4 d) x  x  1. 5 e) x  x  1. 3 2 f) x  x  4. 4 2 g) x  2 x  24 HD: Số hạng cần thêm bớt:. 3 h) x  2 x  4. 4 4 i) a  4b. 2 a) 4 x. 2 c) x  x. b) 16 x. 2. 2 d) x. e) x. 2. f) x. 2. 2 2 2 2 g) 4 x h) 2 x  2 x i) 4a b Bài 6. Phân tích các đa thức sau thành nhân tử: (đặt biến phụ) 2 2 2 a) ( x  x )  14( x  x )  24. 2 2 2 b) ( x  x )  4 x  4 x  12 d) ( x  1)( x  2)( x  3)( x  4)  1. 4 3 2 c) x  2 x  5 x  4 x  12 e) ( x  1)( x  3)( x  5)( x  7)  15. f) ( x  1)( x  2)( x  3)( x  4)  24 Bài 7. Phân tích các đa thức sau thành nhân tử: (đặt biến phụ) 2 2 2 2 a) ( x  4 x  8)  3x ( x  4 x  8)  2 x. 2 2 b) ( x  x  1)( x  x  2)  12. 2 2 c) ( x  8x  7)( x  8x  15)  15. d) ( x  2)( x  3)( x  4)( x  5)  24 VẤN ĐỀ V. Tổng hợp. Bài 1. Phân tích các đa thức sau thành nhân tử: 2 a) x  4 x  3. d). 2 b) 16 x  5 x  3. 2 x2  3x  5. 2 2 2 g) (a  1)  4a. 2 c) 2 x  7 x  5. 3 2 e) x  3 x  1  3 x 3 2 h) x  3 x – 4 x  12. 2 f) x  4 x  5 4 3 i) x  x  x  1. 2 2 4 3 2 k) x – x – x  1 l) (2 x  1) – ( x –1) Bài 2. Phân tích các đa thức sau thành nhân tử:. 4 2 m) x  4 x – 5. 2 2 a)  x  y  x  y. b) x ( x  y )  5 x  5y. 2 2 c) x  5x  5y  y. 3 2 2 d) 5 x  5 x y  10 x  10 xy. 3 3 e) 27 x  8y. 2 2 f) x – y – x – y. 2 2 2 g) x  y  2 xy  y. 2 2 h) x  y  4  4 x. 6 6 i) x  y. 2 2 3 2 3 k) x  3 x  3 x  1 – 27z l) 4 x  4 x – 9 y  1 Bài 3. Phân tích các đa thức sau thành nhân tử:. 2 m) x –3 x  xy –3y. 2 2 2 a) 5 x  10 xy  5y  20 z. 2 2 2 b) x  z  y  2 xy. 3 2 c) a  ay  a x  xy. 2 2 2 d) x  2 xy  4 z  y. 2 2 2 e) 3 x  6 xy  3y  12 z. 2 2 2 f) x  6 xy  25z  9 y. 2 2 2 g) x  y  2 yz  z. 2 2 h) x – 2 xy  y – xz  yz. 2 i) x – 2 xy  tx – 2ty. 2 k) 2 xy  3z  6 y  xz l) x  2 xz  2 xy  4 yz Bài 4. Phân tích các đa thức sau thành nhân tử:. 3 3 3 3 m) ( x  y  z) – x – y – z. 3 2 2 3 a) x  x z  y z  xyz  y. b) bc(b  c)  ca(c  a)  ab(a  b). 2 2 2 c) a (b  c)  b (c  a)  c (a  b). 6 4 3 2 d) a  a  2a  2a.

<span class='text_page_counter'>(6)</span> 3 3 3 3 f) ( x  y  z)  x  y  z. 9 7 6 5 4 3 2 e) x  x  x  x  x  x  x  1. 3 3 3 3 3 3 3 g) (a  b  c)  (a  b  c)  (b  c  a)  (c  a  b) h) x  y  z  3 xyz Bài 5. Giải các phương trình sau: 2 a) ( x  2) –( x – 3)( x  3) 6. 2 b) ( x  3)  (4  x )(4 – x ) 10. 2 c) ( x  4)  (1 – x )(1  x ) 7. 2 d) ( x – 4) –( x – 2)( x  2) 6. 2 e) 4( x – 3) – (2 x –1)(2 x  1) 10. 2 f) 25( x  3)  (1 – 5 x )(1  5 x ) 8. 2 g) 9( x  1) – (3 x – 2)(3 x  2) 10 Bài 6. Chứng minh rằng:. 2 h)  4( x –1)  (2 x –1)(2 x  1)  3. 2 a) a (a  1)  2a(a  1) chia hết cho 6 với a  Z . b) a(2a  3)  2a(a  1) chia hết cho 5 với a  Z . 2 c) x  2 x  2  0 với x  Z . 2 d)  x  4 x  5  0 với x  Z .. IV. CHIA ĐA THỨC VẤN ĐỀ I. Chia đa thức cho đơn thức Bài 1. Thực hiện phép tính: 5 3 a) ( 2) : ( 2). 7 3 b) ( y ) : ( y ). 12 10 c) x : ( x ). 6 3 d) (2 x ) : (2 x ) Bài 2. Thực hiện phép tính:. 5 2 e) ( 3 x ) : ( 3 x ). 2 4 2 2 f) ( xy ) : ( xy ). 9 6 a) ( x  2) : ( x  2) 1 2( x 2  1)3 : ( x 2  1) 3 d) Bài 3. Thực hiện phép tính:. 4 3 b) ( x  y ) : ( x  2) 5 5( x  y )5 : ( x  y )2 6 e). 2 5 2 c) ( x  2 x  4) : ( x  2 x  4). 2 a) 6 xy : 3y. 2 3 2 b) 6 x y : 2 xy. 2 c) 8 x y : 2 xy. 2 5 3 d) 5 x y : xy. 4 3 2 e) ( 4 x y ) : 2 x y. 3 4 3 f) xy z : ( 2 xz ). 3 3 3  1 2 2 x y : x y   2  g) 4. 2 4 3 h) 9 x y z :12 xy. 3 2 3 2 i) (2 x y )(3 xy ) : 2 x y. (3a2b)3 (ab3 )2. (2 xy 2 )3 (3x 2 y )2. (a 2 b 2 )4 k) Bài 4. Thực hiện phép tính: 3 2 a) (2 x  x  5x ) : x. l). (2 x 3 y 2 )2. 4 3 2 b) (3 x  2 x  x ) : ( 2 x ).  1  ( x 3 – 2 x 2 y  3 xy 2 ) :   x   2 . d) Bài 5. Thực hiện phép tính:. 5 2 3 2 c) ( 2 x  3x – 4 x ) : 2 x.  3( x  y )5  2( x  y )4  3( x  y)2  : 5( x  y )2 e) . a) (3 x y  4 x y  5x y ) : 2 x y. 3 6 3 3 3 4 9 5 3 3 ax  : ax  a x  a x  7 10  5 b)  5. 2 3 4 4 2 2 2 c) (9 x y  15 x y ) : 3 x y  (2  3x y ) y. 2 3 2 d) (6 x  xy ) : x  (2 x y  3 xy ) : xy  (2 x  1) x. 5 2. 3 3. 2 4. 2 2. 3 ( x 2  xy ) : x  (6 x 2 y 5  9 x 3y 4  15x 4 y 2 ) : x 2 y 3 2 e).

<span class='text_page_counter'>(7)</span> VẤN ĐỀ II. Chia đa thức cho đa thức Bài 1. Thực hiện phép tính: 3 2 a) ( x – 3 x ) : ( x – 3). 2 b) (2 x  2 x  4) : ( x  2). 4 c) ( x – x –14) : ( x – 2). 3 2 d) ( x  3 x  x  3) : ( x  3). 3 2 e) ( x  x –12) : ( x – 2) 3 2 g) ( 3x  5x  9 x  15) : (5  3x ) Bài 2. Thực hiện phép tính:. 3 2 f) (2 x  5x  6 x –15) : (2 x – 5) 2 3 h) ( x  6 x  26 x  21) : (2 x  3). 4 2 3 2 a) (2 x  5x  x  3  3x ) : ( x  3). 5 3 2 3 b) ( x  x  x  1) : ( x  1). 3 2 2 c) (2 x  5x – 2 x  3) : (2 x – x  1). 3 2 4 2 d) (8x  8x  10 x  3x  5) : (3 x  2 x  1). 3 4 2 2 e) ( x  2 x  4  x  7 x ) : ( x  x  1) Bài 3. Thực hiện phép tính: 2 2 a) (5 x  9 xy  2 y ) : ( x  2 y). 4 3 2 2 3 2 2 b) ( x  x y  x y  xy ) : ( x  y ). 5 4 5 4 3 2 3 3 2 3 2 2 3 c) (4 x  3 xy  y  2 x y  6 x y ) : (2 x  y  2 xy ) d) (2a  7ab  7a b  2b ) : (2 a  b) Bài 4. Thực hiện phép tính: 2 3 2 2 a) (2 x  4 y ) : ( x  2 y )  (9 x  12 x  3x ) : ( 3 x )  3( x  3) 2 2 4 4 3 3 2 2 b) (13x y  5x  6 y  13x y  13xy ) : (2 y  x  3xy ) Bài 5. Tìm a, b để đa thức f ( x ) chia hết cho đa thức g( x ) , với: 4 3 2 2 a) f ( x ) x  9 x  21x  ax  b , g( x )  x  x  2 4 3 2 2 b) f ( x ) x  x  6 x  x  a , g( x ) x  x  5 3 2 c) f ( x ) 3 x  10 x  5  a , g( x ) 3 x  1 3 2 d) f ( x )  x – 3 x  a , g( x ) ( x –1) ĐS: a) a 1, b  30. Bài 6. Thực hiện phép chia f ( x ) cho g( x ) để tìm thương và dư: 3 2 2 a) f ( x ) 4 x  3 x  1 , g( x ) x  2 x  1 4 2 3 2 b) f ( x ) 2  4 x  3 x  7 x  5x , g( x ) 1  x  x 2 3 4 2 c) f ( x ) 19 x  11x  9  20 x  2 x , g( x ) 1  x  4 x 4 5 3 2 2 3 2 2 3 4 3 2 2 d) f ( x ) 3x y  x  3x y  x y  x y  2 xy  y , g( x )  x  x y  y. VẤN ĐỀ III. Tìm đa thức bằng phương pháp hệ số bất định Bài 1. Cho biết đa thức f ( x ) chia hết cho đa thức g( x ) . Tìm đa thức thương: 3 2 a) f ( x ) x  5 x  11x  10 , g( x )  x  2. 2 ĐS: q( x ) x  3 x  5. 3 2 b) f ( x ) 3 x  7 x  4 x  4 , g( x )  x  2. 2 ĐS: q( x ) 3 x  x  2. 4 3 Bài 2. Phân tích đa thức P( x ) x  x  2 x  4 thành nhân tử, biết rằng một nhân tử có dạng:. x 2  dx  2 . 2 2 ĐS: P( x ) ( x  x  2)( x  2) ..

<span class='text_page_counter'>(8)</span> 3 2 2 Bài 3. Với giá trị nào của a và b thì đa thức x  ax  2 x  b chia hết cho đa thức x  x  1 . ĐS: a 2, b 1 .. Bài 4. Phân tích các đa thức sau thành nhân tử: 3 2 a) x  x  14 x  24. 3 2 b) x  4 x  4 x  3. 3 c) x  7 x  6. 3 d) x  19 x  30. 3 2 e) a  6a  11a  6 Bài 5. Tìm các giá trị a, b, k để đa thức f ( x ) chia hết cho đa thức g( x ) : 4 3 2 2 a) f ( x ) x  9 x  21x  x  k , g( x )  x  x  2 .. ĐS: k  30 .. 4 3 2 2 b) f ( x )  x  3x  3 x  ax  b , g( x )  x  3 x  4 .. ĐS: a 3, b  4 .. 3 2 Bài 6. Tìm tất cả các số tự nhiên k để cho đa thức f (k ) k  2k  15 chia hết cho nhị thức g(k ) k  3 . ĐS: k 0, k 3 .. BÀI TẬP ÔN CHƯƠNG I Bài 1. Thực hiện phép tính: 3 2 2 a) (3x  2 x  x  2).(5x ) 2 2 c) (3x  5x  2)(2 x  4 x  3) Bài 2. Rút gọn các biểu thức sau:. 2 3 3 b) (a x  5 x  3a).( 2a x ) 4 3 2 2 3 4 d) (a  a b  a b  ab  b )(a  b). 2 2 a) (a  a  1)(a  a  1). 2 2 b) (a  2)(a  2)(a  2a  4)(a  2a  4). 2 2 3 3 3 2 c) (2  3y)  (2 x  3y)  12 xy d) ( x  1)  ( x  1)  ( x  1)  ( x  1)( x  x  1) Bài 3. Trong các biểu thức sau, biểu thức nào không phụ thuộc vào x: 3 3 a) ( x  1)  ( x  1)  6( x  1)( x  1). 2 2 b) ( x  1)( x  x  1)  ( x  1)( x  x  1). 2 c) ( x  2)  ( x  3)( x  1). 2 2 d) ( x  1)( x  x  1)  ( x  1)( x  x  1). 3 3 e) ( x  1)  ( x  1)  6( x  1)( x  1) Bài 4. Tính giá trị của các biểu thức sau:. 2 2 f) ( x  3)  ( x  3)  12 x. 3 3 2 2 3 2 a) A a  3a  3a  4 với a 11 b) B 2( x  y )  3( x  y ) với x  y 1 Bài 5. Phân tích các đa thức sau thành nhân tử: 2 2 a) 1  2 xy  x  y. 2 2 2 2 b) a  b  c  d  2ab  2cd. 3 3 c) a b  1. 2 2 2 d) x ( y  z)  y ( z  x )  z ( x  y). 2 e) x  15x  36. 12 6 6 12 f) x  3 x y  2 y. 2 2 8 2 g) x  64 x h) ( x  8)  784 Bài 6. Thực hiện phép chia các đa thức sau: (đặt phép chia vào bài) 3 2 a) (35x  41x  13x  5) : (5x  2). 4 3 2 2 b) ( x  6 x  16 x  22 x  15) : ( x  2 x  3). 4 3 2 2 3 2 2 4 3 2 2 4 2 2 c) ( x  x y  x y  xy ) : ( x  y ) d) (4 x  14 x y  24 x y  54 y ) : ( x  3 xy  9 y ) Bài 7. Thực hiện phép chia các đa thức sau: 4 3 2 2 a) (3x  8x  10 x  8x  5) : (3 x  2 x  1) 3 2 2 b) (2 x  9 x  19 x  15) : ( x  3 x  5) 4 3 2 2 c) (15x  x  x  41x  70) : (3x  2 x  7) 5 4 3 2 2 3 4 5 3 2 3 d) (6 x  3x y  2 x y  4 x y  5xy  2 y ) : (3x  2 xy  y ).

<span class='text_page_counter'>(9)</span> Bài 8. Giải các phương trình sau: 3 a) x  16 x 0. 3 b) 2 x  50 x 0. 2 2 2 2 2 d) 5 x  4( x  2 x  1)  5 0 e) ( x  9)  ( x  3) 0. 3 2 c) x  4 x  9 x  36 0 3 f) x  3 x  2 0. 3 2 g) (2 x  3)( x  1)  (4 x  6 x  6 x ) : ( 2 x ) 18 Bài 9. Chứng minh rằng: 2 2 a) a  2a  b  1 0 với mọi giá trị của a và b. 2 2 b) x  y  2 xy  4  0 với mọi giá trị của x và y. c) ( x  3)( x  5)  2  0 với mọi giá trị của x.. Bài 10.Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của các biểu thức sau: 2 a) x  x  1. 2 b) 2  x  x. 2 c) x  4 x  1. 2 d) 4 x  4 x  11 g) h(h  1)(h  2)(h  3). 2 e) 3 x  6 x  1. 2 2 f) x  2 x  y  4 y  6.

<span class='text_page_counter'>(10)</span>