Tải bản đầy đủ (.ppt) (22 trang)
  1. Trang chủ
    2. >>
  2. Đề thi
    3. >>
  3. Đề thi lớp 1

Tu giac noi tiep

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (341.86 KB, 22 trang )

<span class='text_page_counter'>(1)</span>TẤT CẢ VÌ HỌC SINH THÂN YÊU.

<span class='text_page_counter'>(2)</span>

<span class='text_page_counter'>(3)</span> Bài cũ: Câu 1: a)Phát biểu định nghiã về góc nội tiếp b)Hình nào sau đây có góc nội tiếp ? Nêu tên các góc đó.. H. C A. D B. E K. G.

<span class='text_page_counter'>(4)</span> Đáp:. H. C A. D B. E K. G. Góc nội tiếp là :HEK , EHG.

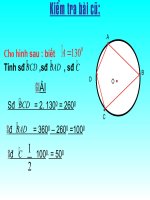
<span class='text_page_counter'>(5)</span> BÀI CŨ : Câu 2: a)Nêu định lí về tổng các góc trong một tứgiác b)Tính các góc của tứ giác ABCD biết :. ˆ :B ˆ :D ˆ :C ˆ 1 : 2 : 4 : 5 A Đáp: b). ˆ Bˆ Cˆ D ˆ  Bˆ  Cˆ  D ˆ A ˆ 360 0 A      300 1 2 4 5 1 2  4  5 12 ˆ 300 , Bˆ 600 , Cˆ 1200 , D ˆ 1500  A.

<span class='text_page_counter'>(6)</span> 1.. KHÁI NIỆM TỨ GIÁC NỘI TIẾP. ?1 a) Vẽ đường tròn tâm 0 rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó..

<span class='text_page_counter'>(7)</span> B A O D. C.

<span class='text_page_counter'>(8)</span> ?1. b)Vẽ đường tròn tâm I rồi vẽ một tứ giác có ba đỉnh nằm trên đường tròn đó còn một đỉnh thì không ..

<span class='text_page_counter'>(9)</span> Q. P Q. P I N. N. M. I M. Các tứ giác trong hình trên không phải tứ giác nội tiếp được đường tròn.

<span class='text_page_counter'>(10)</span> TỨ GIÁC NỘI TIẾP B A O D. C. Tứ giác ABCD có các đỉnh nằm trên đường tròn nên gọi là tứ giác nội tiếp được đường tròn ..

<span class='text_page_counter'>(11)</span> TỨ GIÁC NỘI TIẾP. Góc. A D B C mCDA = 88.79 mABC = 73.52. Số đo. CDA 88 69’ 0. ABC 730 52’ Tổng 162 51’ 0.

<span class='text_page_counter'>(12)</span> TỨ GIÁC NỘI TIẾP F. Góc. E. Số đo. EFG 105 17’ 0. G. H. mEFG = 105.17 mGHE = 74.83. GHE. 74 43’ 0. Tổng 1800.

<span class='text_page_counter'>(13)</span> TỨ GIÁC NỘI TIẾP 2. Định lí : Trong một tứ giác nội tiếp , tổng số đo hai góc đối nhau bằng 1800 B. A. BAD +BCD = 1800. O. ABD + ADC = 1800. D C.

<span class='text_page_counter'>(14)</span> TỨ GIÁC NỘI TIẾP Chứng. minh :. B. A O. SđBAD = 1/2SđBCD Sđ BCD = 1/2SđBAD. D. SđBAD +SđBCD = 1/2SđBCD + 1/2SđBAD = 1/2Sđ (O) = 1/2 . 3600= 1800. C.

<span class='text_page_counter'>(15)</span> TỨ GIÁC NỘI TIẾP N. Bài tập:. 700. Cho tứ giác ABCD nội. O. tiếp được đường tròn có QMN= 1v, MNP = 70 Tính các góc còn lại .. M 0. ? ? Q. P.

<span class='text_page_counter'>(16)</span> TỨ GIÁC NỘI TIẾP Đáp:. Vì MNPQ nội tiếp nên:. N. QPN = 900. 700 O M. ? ? Q. MNP + MQP = 1800. P Vậy: MQP = 1800-MNP = 1800 – 700=1100.

<span class='text_page_counter'>(17)</span> 3. Định lí đảo: Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 1800 thì tứ giác đó nội tiếp được đường tròn .. B. A O. m. D. C.

<span class='text_page_counter'>(18)</span> TỨ GIÁC NỘI TIẾP 3. Định lí đảo: Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 1800 thì tứ giác đó nội tiếp được đường tròn .. B. A O. m. D. C.

<span class='text_page_counter'>(19)</span> Bài tập : A. Cho tam giác ABC đều, gọi M , N trung điểm của AB , AC. Chứng minh tứ giác BMNC nội tiếp được đường tròn .. M. B. N. C.

<span class='text_page_counter'>(20)</span> Bài giải:. . A. M. N. Vì M,N là trung điểm của AB , CD nên MN là đường trung bình của tam giác ABC . Suy ra : MN // BC. VìABC =600 nên BMN = 1200 Vậy : BMN + BCN = 1800. B. C. Do đó tứ giác BMNC nội tiếp được đường tròn.

<span class='text_page_counter'>(21)</span> Hướng dẫn về nhà:. Bài 58 trg90 sgk:. A. O B. C D.

<span class='text_page_counter'>(22)</span> Hướng dẫndẫn về nhà: Hướng về nhà:. A B. Bài 59 trg 90 sgk :. D. O. P. C.

<span class='text_page_counter'>(23)</span>

Tài liệu liên quan

Tài liệu bạn tìm kiếm đã sẵn sàng tải về

Tải bản đầy đủ ngay
×