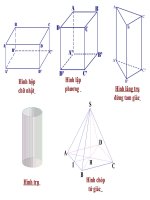
Chu de 7 HINH LANG TRU DUNG HINH CHOP DEU

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (279.08 KB, 4 trang )

(1)<div class='page_container' data-page=1>

Chủ đề 7: HèNH LĂNG TRỤ ĐỨNG. HèNH CHểP ĐỀU !

A - hình lăng trụ đứng

I-H×nh hép chữ nhật
1. Hình hộp chữ nhật

Mt hỡnh hp ch nht có 6 mặt, mỗi mặt đều là hình chữ nhật (cùng với các điểm trong của nó).
Một hình hộp chữ nht cú 8 nh,12 cnh.

Hai mặt của hình hộp chữ nhật không có cạnh chung gọi là

hai mt i diện, có thể xem đó là hai mặt đáy của hình hộp
chữ nhật, khi đó các mặt cịn lại đợc xem là các mặt bên.
VD: Hỡnh bờn cạnh cú:

- Các mặt của hình hộp chữ nhật là: ABCD, A'B'C 'D', ABB'A',
 BCC 'B', ...

- Các đỉnh của hình hộp chữ nhật là: A, B, C, D, A', B', C ', D'.
- Các cạnh của hình hộp chữ nhật là: AB, BC, CD, DA, AA',
BB', ...

- Hai đáy của hình hộp là: ABCD và A'B'C 'D', khi đó chiều cao tơng ứng là AA'.

Hình lập phương là hình hộp chữ nhật có 6 mặt là những hình vng.
2. Hai ® ờng thẳng song song trong không gian.

Trong khụng gian, hai đường thẳng a và b gọi là song song với nhau nếu chúng nằm trong cùng
một mặt phẳng. Chẳng hạn, các đường thẳng AA’ và BB’ song song với nhau.

 Với hai đường thẳng phân biệt a, b trong khơng gian có thể xảy ra các
khả năng sau:

 Cắt nhau: chẳng hạn, D’C’ và CC’ cắt nhau tại C’ và chúng cùng nằm
trong mặt phẳng (DCC’D’).

 Song song: chẳng hạn, AA’ song song với DD’, ký hiệu là AA’// DD’
và chúng cùng nằm trong mặt phẳng (AA’D’D).

 Không cùng nằm trong một mặt phẳng nào: chẳng hạn, các đường
thẳng AD và D’C’.

 Hai đường thẳng phân biệt, cùng song song với một đường thẳng thứ 3 thì chúng song song với
nhau. Chẳng hạn, AB và D’C’ song song vì chúng cùng song song với DC.

3.

Đường thẳng song song với mặt phẳng. Hai mặt phẳng song song.

 Khi AB không nằm trong mặt phẳng (A’B’C’D’) mà AB song song với một đường thẳng của
mặt phẳng này, chẳng hạn AB// A’B’, thì người ta nói: AB song song với mặt phẳng (A’B’C’D’)
và được ký hiệu là: AB// mp(A’B’C’D’).

 Trên hình hộp chữ nhật, xét hai mặt phẳng (ABCD) và (A’B’C’D’).
-Mặt phẳng (ABCD) chứa hai đường thẳng cắt nhau: AB và AD.
-Mặt phẳng (A’B’C’D’) chứa hai đường thẳng cắt nhau: A’B’ và A’D’

Hơn nữa, AB song song với A’B’, AD song song với A’D’.Do đó, người ta nói: mặt phẳng

(ABCD) song song với mặt phẳng (A’B’C’D’) và được ký hiệu là: mp(ABCD)// 
mp(A’B’C’D’).

Nhận xét:

Nếu một đường thẳng song song với một mặt phẳng thì chúng khơng có điểm chung.
Hai mặt phẳng song song thì khơng có điểm chung.

Hai mặt phẳng phân biệt có một điểm chung thì chúng có chung một đường thẳng đi qua điểm
đó. Khi đó, ta nói: hai mặt phẳng này cắt nhau.

II- DiƯn tÝch xung quanh CỦAh×nh HỘP CHỮ NHẬT

Diện tích xung quanh của hình hộp chữ nhật bằng chu vi đáy nhân với chiều cao.
Sxq

= 2p .h

</div>
(2)<div class='page_container' data-page=2>

Diện tích tồn phần của hình hộp chữ nhật bằng tổng của diện tích xung quanh và diện tích 2
đáy: Stp

= S

xq

+ 2. S

đ

 Đặc biệt với hình lập phương, ta có: Sxq

= S

đ

.4

; S

tp

= S

.6

III- Thể tích hình hộp chữ nhật

1.

Đ ờng thẳng vuông góc với mặt phẳng - Hai mặt phẳng
vuông góc

Khi ng thẳng A’A cùng vng góc với hai đường thẳng
cắt nhau là AD và AB của mặt phẳng (ABCD) thì ta nói:
A’A vng góc với mặt phẳng (ABCD) tại A và được ký
hiệu là:

A

'

A

⊥

mp

(

ABCD

)

Nếu một đường thẳng vng góc với một mặt phẳng tại

điểm A thì nó vng góc với mọi đường thẳng đi qua A và nằm trong mặt phẳng đó.

Khi một trong hai mặt phẳng chứa một đường thẳng vuông góc với mặt phẳng cịn lại thì người
ta nói: hai mặt phẳng đó vng góc với nhau và được ký hiệu là ( chẳng hạn là với trường hợp
vừa xét):

mp

(

ADD ' A '

)

mp

(

ABCD

)

2. Thể tích hình hộp chữ nhật: V =

a.b.c

-Thể tích hình lập phương

: V = a

3

IV- hình lăng trụ đứng

Hỡnh lăng trụ đứng cũn gọi tắt là lăng trụ đứng. Trong hỡnh bờn, ta cú:
 A, B, C, D, A1, B1, C1, D1 là các đỉnh.

 ABB1A1, BCC1B1 , là nhng hình chữ nhật. Chỳng c gi l cỏc mt

bờn.

Đoạn AA1, BB1, CC1song song và bằng nhau là các cạnh bên.

Hai mt: ABCD, A1 B1C1D1 l hai đáy. Hai đáy của lăng trụ là 2 mặt phẳng

song song.

 Độ dài cạnh bên đợc gọi là chiều cao.

Đáy là tam giác, tứ giác, ngũ giác ta gọi là lăng trụ tam giác, lăng trụ tứ
giác, lăng trơ ngị gi¸c.

*Hình chữ nhật, hình vng là các dạng đặc biệt của hình bình hành nờn chỳng
cũng là những lăng trụ đứng.

* Hình lăng trụ đứng có đáy là hình bình hành đợc gọi là hình hộp đứng.
Chú ý:

- Các mặt bên là những hình chữ nhật nên khi vẽ nó trên mặt phẳng, ta thường
vẽ thành hình bình hành.

- Các cạnh song song, ta thường vẽ thành các on thng song song.
- Các cạnh vuông góc có thể khơng vÏ thành các đoạn thẳng vu«ng gãc.

-Cỏc đường nằm ẩn phớa trong khụng nhỡn thấy, thỡ phải vẽ bằng đường nột đứt.
V- Diện tích xung quanh CỦAhình lăng trụ đứng

Diện tích xung quanh của hình lăng trụ đứng bằng chu vi đáy nhân với
chiều cao.

Sxq

= 2p .h

( Trong đó: p là nửa chu vi đáy, h là chiều cao).

</div>
(3)<div class='page_container' data-page=3>

Stp

= S

xq

+ 2. S

đ

VI- Thể tích hình lăng trụ đứng

1.C«ng thøc tÝnh thĨ tÝch

:

Thể tích hình lăng trụ đứng bằng diện
tích đáy nhân với chiều cao.

V = S

đ

. h

( Trong đú: Sđ là diện tích đáy, h là chiều cao )

B- HÌNH CHĨP ĐỀU

i-hình chóp đều và hình chóp cụt đều
1. Hình chóp là hỡnh cú đồng thi cc yu t sau:

o Đáy là một đa giác.

o Các mặt bên là các tam giác có chung 1 nh.

o SAB, SBC, SCD, SDA là các mặt bên.

o SH  mp(ABCD) là đờng cao.

o S là đỉnh.

o Mặt đáy: ABCD

 Hình chóp S.ABCD có đỉnh là S, đáy là t giỏc ABCD, ta gi l

hình chóp tứ giác.

2.Hỡnh chóp đều là hỡnh chúp cú đồng thời cỏc yếu tố sau:
o Đáy là một đa giác đều.

o Các mặt bên là các tam giác cân bằng nhau.
o Đờng cao trùng với tâm của đáy.

 Hình chóp tứ giác đều : có mặt đáy là hình vng, các mặt
bên là các tam giác cân.

 Chân đờng cao H là tâm của đờng tròn đi qua các đỉnh của
mặt đáy

 Đờng cao vẽ từ đỉnh S của mỗi mặt bên của hình chóp đều
gọi là trung đoạn của hình chóp đó. Trung đoạn của hình chóp
khơng vng góc với mặt phẳng đáy, chỉ vng góc cạnh đáy
của hình chóp.

3. Hình chóp cụt đều

Cắt hình chóp đều bằng một mặt phẳng song song với đáy. Ta
được phần hỡnh chúp nằm giữa mặt phẳng đú và mặt phẳng đỏy
của hỡnh chúp gọi là hỡnh chúp cụt đều.

- Hai đáy của hình chóp cụt đều song song với nhau.
- Các mặt bên của hình chóp cụt đều là các hình thang cân.

- Hình chóp cụt đều có hai mặt đáy là 2 đa giác đều, đồng dạng với nhau.

Chóp tam giác

đều Chóp tứ giác đều Chóp ngũ giác đều Chóp lục giác đều
Đáy Tam giác đều Hình vng Ngũ giác đều Lục giác đều
Mặt bên Tam giác cân Tam giác cân Tam giác cân Tam giác cân

Số cạnh đáy 3 4 5 6

Sè c¹nh 6 8 10 12

Sè mỈt 4 5 6 7

II- Diện tích xung quanh hình chóp đều

Diện tích xung quanh của hình chóp đều: bằng tích của nửa chu vi đáy với trung đoạn.
S xq

= p. d

( p là nửa chu vi đáy, d là trung đoạn của hình chóp đều)

</div>
(4)<div class='page_container' data-page=4>

III-Thể tích của hình chóp đều
V =

S

đ

. h

(Sđ là diện tích đáy, h là chiều cao)

VUI TỐN HỌC !

 Tìm tên một nhà tốn học Việt Nam thời trước.

Em hãy tính các tích sau rồi viết chữ tương ứng với đáp số đúng vào các ơ
trống. Khi đó em sẽ biết được tên của một nhà toán học Việt Nam nổi tiếng ở
thế kỷ XV.

T∘−2

3 ⋅

−3

4 E∘

16
17⋅

−17

32 G∘

15
49⋅

−84

N∘−5

16 ⋅

−18

5 V∘

7
6⋅

14 U∘

7⋅1 L∘

−5⋅

1
3

H∘13

19⋅

−19

13 O∘

1
2⋅

3
4⋅

−8

9 I∘

6
11⋅

−1

7 ⋅0⋅
3
29
1

−5

−1

−36

-1 3 9

8
6

9
8

1
2

−1

0 -1

 “Tỉ số vàng”

Người Cổ Hy Lạp và người Cổ Ai Cập đã ý thức được những tỉ số “đẹp” trong các cơng trình xây
dựng. Họ cho rằng hình chữ nhật đẹp là hình chữ nhật có tỉ số giữa chiều dài và chiều rộng là

1: 0,618. Vì thế, tỉ số này được gọi là “tỉ số vàng” ( theo cách gọi của nhà danh họa và nhà khoa học
người Ý nổi tiếng Lê –ô–nác –đô đa Vin–xi).

</div>