Tải bản đầy đủ (.ppt) (12 trang)
  1. Trang chủ
    2. >>
  2. Đề thi
    3. >>
  3. Đề thi lớp 5

TU GIAC NOI TIEP

Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (660.15 KB, 12 trang )

<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>

HÌNH HỌC 9


<i><b>§7: </b></i>



<i><b>§7: </b></i>

<i><b>TỨ GIÁC NỘI TIẾP</b></i>

<i><b><sub>TỨ GIÁC NỘI TIẾP</sub></b></i>


<b>THCS TRIỆU NGUYÊN</b>


</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

B



C



D


A



O



300 400


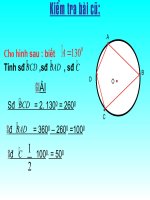
Tính:

ADC = ?
ABC+ ADC =?


0


30





<i>BAC</i>

<i>BCA</i>

40

0


<b>Bài tập: Cho hình bên, biết</b>


</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

<i><b>§7</b></i>




<i><b>§7</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



<b>1. Khái niệm tứ giác nội tiếp</b>



<b>1. Khái niệm tứ giác nội tiếp</b>



<b>Các em suy nghĩ làm việc cá nhân </b> <b>?1</b>
<b>?1</b>


<b>a)</b>


<b>a)</b> <b>Vẽ đường tròn tâm O rồi vẽ một tứ giác có tất cảVẽ đường trịn tâm O rồi vẽ một tứ giác có tất cả</b>
<b>các đỉnh nằm trên đường trịn đó.</b>


<b>các đỉnh nằm trên đường trịn đó.</b>


<b>b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba</b>


<b>b) Vẽ một đường trịn tâm I rồi vẽ một tứ giác có ba</b>


<b>đỉnh nằm trên đường trịn cịn đỉnh thứ tư thì khơng.</b>


<b>đỉnh nằm trên đường trịn cịn đỉnh thứ tư thì khơng.</b>


<i><b>Định nghĩa:</b></i>


<i><b>Định nghĩa:</b></i> <b>Một tứ giác có bốn đỉnh nằm trên một đường trịnMột tứ giác có bốn đỉnh nằm trên một đường trịn<sub>được gọi là tứ giác nội tiếp đường tròn (gọi tắt là</sub><sub>được gọi là tứ giác nội tiếp đường tròn (gọi tắt là</sub></b>


<b>tứ giác nội tiếp)</b>



<b>tứ giác nội tiếp)</b>


<i><b>Ví dụ:</b></i>


<i><b>Ví dụ:</b></i> <i>Trong các tứ giác sau, tứ giác nào là tứ giác nội tiếp, Trong các tứ giác sau, tứ giác nào là tứ giác nội tiếp, </i>


<i>tứ giác nào không là tứ giác nội tiếp ? vì sao?</i>


<i>tứ giác nào khơng là tứ giác nội tiếp ? vì sao?</i>


<b>O</b>
<b>C</b>
<b>D</b>
<b>A</b>
<b>B</b>
<i>Hình 43</i>
<i>Hình 43</i>
<b>M</b>
<b>N</b>
<b>I</b>
<b>Q</b>
<b>P</b>
<i>Hình 44</i>
<i>Hình 44</i>
<i><b>Tứ giác </b></i>
<i><b>Tứ giác </b></i>
<i><b>nội tiếp</b></i>
<i><b>nội tiếp</b></i>
<b>Q</b>


<b>I</b>
<b>N</b>
<b>M</b>
<b>P</b>


<i><b>a)</b></i> <i><b>Tứ giác </b></i> <i><b>b)</b></i>


</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

<b>DỰ ĐOÁN VỀ TỔNG SỐ ĐO HAI GÓC </b>


<b>ĐỐI DIỆN CỦA TỨ GIÁC NỘI TIẾP</b>



<b>A</b>


<b>B</b>


<b>C</b>
<b>D</b>


<b>N</b>


<b>Q</b>
<b>M</b>


<b>P</b> <b>N</b>


<b>Q</b>
<b>M</b>


<b>O</b> <b>O</b>


<b>P</b>



</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

<i><b>§7</b></i>



<i><b>§7</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



<b>2. Định lý.</b>



<b>2. Định lý.</b>



<i>Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau</i>


<i>Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau</i>


<i>bằng 180</i>


<i>bằng 18000</i>


<i><b>Định lý:</b></i>
<i><b>Định lý:</b></i>
<b>Chứng minh</b>
<b>O</b>
<b>A</b>
<b>B</b>
<b>C</b>
<b>D</b>


<b>Tứ giác ABCD nội tiếp đường trịn (0) </b>
<b>nên ta có:</b>


0


0

<sub>180</sub>


360


.


2


1





<i>A</i>

<i>C</i>



2


1



A = sđ cungBCD; C = sđ cungBAD
=> A + C = (sđ cungBCD + sđ cungBAD)


Tương tự B + D =

<sub>180</sub>

0

2



1

2



</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

<i><b>§7</b></i>



<i><b>§7</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



<b>Định lý đảo:</b> <i><b>Nếu một tứ giác có tổng số đo hai góc đối di</b><b>Ưn</b><b> bằng </b></i>


<i><b>180</b><b>0</b><b> thì tứ giác đó nội tiếp được đường trịn.</b></i>


<b>3. Định lý đảo</b>




<b>3. Định lý đảo</b>



O


B
A


D <sub>C</sub>


<b>m</b>


<b>Chứng minh</b>


Vẽ (0) đi qua 3 điểm A, B, C


=> Cung AmC là cung chứa góc (180 - B)
dựng trên đoạn thẳng AC.


Mặt khác D = 180 - B


Vậy D nằm trên cung AmC. Tứ giác ABCD
nội tiếp (0)


</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

<i><b>§7</b></i>



<i><b>§7</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



Trường hợp



Góc 1) 2) 3)


A <sub>80</sub><sub>0</sub> <sub>60</sub><sub>0</sub>


B <sub>70</sub>0


C <sub>105</sub>0


D


750
1100


1050


1000 <sub>120</sub><sub>0</sub>


750


1800<sub>-x</sub>


(00<sub><x<180</sub>0<sub>)</sub>


<i><b> Bài tập 53 (trang 89-SGK)B</b><b>iÕt ABCD lµ tø giác nội tiếp.</b></i>
<i><b>HÃy điền vào ô trống trong bảng sau:</b></i>


x


0
0



0


0
0
0


</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

<i><b>§7</b></i>



<i><b>§7</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



<i><b>Trong các hình sau, hình nào nội tiếp được đường trịn:</b></i>


<i><b>Hình bình hành</b></i>
<i><b>Hình thoi</b></i>
<i><b>Hình thang</b></i>


<i><b>Hình thang cân</b></i>


<i><b>Hình vng</b></i>
<i><b>Hình chữ nht</b></i>


</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

<i><b>Bài 3</b></i><b>: Cho hình vẽ . HÃy tìm trên hình vẽ các tứ giác nội tiếp?</b>


<b><sub>. </sub></b>

<sub>Bài tập:</sub>


<b><sub>Các tứ giác nội tiếp có trong hình </sub></b>


<b>vẽ lµ: </b>



AEHF , BFEC.


I


H
F


A


B <sub>C</sub>


E


</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

<i><b>Bµi 4</b></i><b>: Cho h×nh vÏ, biÕt xAD = C. Chøng minh tø giác ABCD </b>
<b>nội tiếp.</b>


<b>A</b>


<b>B</b>


<b>C</b>
<b>D</b>


<b><sub>. </sub></b>

<sub>Bài tập:</sub>


<b>x</b>


<b>Chứng minh:</b>


<b>O</b>



<b>Vì xAD kề bù víi DAB </b>


<b>=> xAD + DAB = 1800<sub> (t/c hai gãc kỊ bï)</sub></b>


<b>Mµ xAD = C (gt)</b>
<b>=> C + DAB = 1800</b>


</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

<i><b>TIẾT 48</b></i>



<i><b>TIẾT 48</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>

<i><b>: TỨ GIÁC NỘI TIẾP</b></i>



<i><b>H</b><b>ƯỚNG DẪN VỀ NHÀ</b><b>:</b></i>


<i><b>1. Định nghĩa tứ giác nội tiếp;</b></i>
<i><b>2. Tính chất của tứ giác nội tiếp;</b></i>


<i><b>3. Dấu hiệu nhận biết tứ giác nội tiếp (Định nghĩa và Định lý 3).</b></i>
<i><b>I. NẮM CHẮC:</b></i>


<i><b>II. VẬN DỤNG LÝ THUYẾT GIẢI CÁC BÀI TẬP:</b></i>
<i><b>1. Bài tập: 54, 55 (Sách giáo khoa trang 89);</b></i>


</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12></div>

<!--links-->

Tài liệu liên quan

Tài liệu bạn tìm kiếm đã sẵn sàng tải về

Tải bản đầy đủ ngay
×