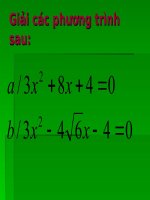<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>



  




<b>Trường THPT Lai Uyên</b>

<b>Bài giảng</b>

<b>Giáo viên: TRƯƠNG QUỐC BẢO</b>

</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

<b>KiÓm tra bài cũ :</b>

1. Giải ph ơng trình bằng cách dùng c«ng thøc nghiƯm :
a) 3x2_{+ 8x + 4 = 0}

b) 3<i>x</i>2  4 6<i>x</i>  4 0

</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

Đối với ph ơng trình ax2_{+ bx + c = 0 ( a}__{0 ) vµ biƯt thøc}__{= b}2_{– 4ac:}
• _NÕu__{> 0 thì ph ơng trình bậc hai có hai nghiƯm ph©n biƯt:}

x₁ = ; x₂ =

ã _Nếu_{= 0 thì ph ơng trình có nghiệm kép x}₁_{= x}₂₌
ã _Nếu_{< 0 thì ph ơng trình vô nghiệm.}

b
2a

  b

2a

  

b
2a



</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

Em hãy nhắc lại 1 số cách giải
ph ơng trình bậc 2 đã học ?

-Cách 1 : đ a ph ơng trình bậc hai về ph ơng trình tích
- Cách 2 : Giải bằng ph ơng pháp vẽ đồ thị Parbol và
đ ờng thẳng để tìm toạ độ điểm chung. Giá trị hồnh độ
tìm đ ợc là nghiệm của ph ơng trình

-Cách 3 : Dùng hằng đẳng thức bình ph ơng của 1 tổng
(hoặc 1 hiệu) . Biến đổi ph ơng trình về dạng

số để lập luận

</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

? Trong các cách nêu đó , cách
nào áp dụng gii c cho tt c

mọi ph ơng trình bậc 2 mà em
thấy dễ áp dụng nhất .

Trong tr ờng hợp hệ số b là số chẵn ta còn
có công thức nghiệm ngắn gọn hơn , giải ra
nghiệm nhanh hơn .

</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

<b>công thøc nghiƯm thu gän</b>

<b>1) C«ng thøc nghiƯm thu gän</b>

Ph ơng trình ax2_{+ bx + c = 0 .Nếu hệ số b chẵn đặt}_{b = 2b’}

T
Ý
n
h




t
h
e
o
h
Ö
s
è
b
’
?


2

₄

_{(2 ')}

2

₄

_{4 '}

2

₄

_{4( '}

2

₎

<i>b</i>

<i>ac</i>

<i>b</i>

<i>ac</i>

<i>b</i>

<i>ac</i>

<i>b</i>

<i>ac</i>

 









Đặt có : ' <i>b</i> '2  <i>ac</i>   4 '

* NÕu  > 0  ’… > 0 th× ph ơng trình có hai nghiệm phân biệt:

Em hóy xột mối quan hệ dấu của
và . Từ đó xét nghiệm
của ph ơng trình theo ?

'





'



1
2
<i>b</i>
<i>x</i>
<i>a</i>
  

  ... 2 ... _

2a

-2b’ ’  b ' '

a 2

2 ' 2 '

;
2
'
2
'
<i>b</i>
<i>x</i>
<i>a</i>
<i>b</i>
<i>a</i>
<i>a</i>
<i>b</i>
  
      

* NÕu  = 0 = 0 thì ph ơng trình cã nghiÖm kÐp

 ’
1 2

2

2

<i>b</i>

<i>x</i>

<i>x</i>

<i>a</i>

<i>a</i>









-2b’



-b’

a

</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

Qua kết quả suy luận trên , em hÃy
tóm tắt lại công thức nghiệm thu
gọn?

<b>* C«ng thøc nghiƯm thu gän </b>: SGK T 48

<b>C«ng thøc nghiƯm :</b>

*NÕu ph ¬ng trình có hai
nghiệm phân biệt :

*NÕu ph ¬ng tr×nh cã
nghiƯm kÐp:

* NÕu ph ơng trình vô
nghiệm

<b>Công thức nghiệm thu gọn:</b>

*Nếu ph ơng trình có hai
nghiƯm ph©n biƯt :

*Nếu ph ơng trình cã
nghiÖm kÐp:

* NÕu ph ơng trình vô
nghiệm

Ph ơng trình ax2 _{+ bx + c = 0}

(

<i>a</i>



0) :

0

 

1 ; 2

2 2
<i>b</i> <i>b</i>
<i>x</i> <i>x</i>
<i>a</i> <i>a</i>
     
 
0
 
1 2
2
<i>b</i>
<i>x</i> <i>x</i>
<i>a</i>


 
0
 
' 0
 
1 2
' ' ' '
;
<i>b</i> <i>b</i>
<i>x</i> <i>x</i>
<i>a</i> <i>a</i>
     
 
' 0
 
1 2
'
<i>b</i>
<i>x</i> <i>x</i>
<i>a</i>

 
' 0
 
2 ₄
<i>b</i> <i>ac</i>

</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

<b>2) Bài tập áp dụng :</b>

Giải ph ơng trình bằng công thức nghiệm thu gọn

2

)3 8 4 0

<i>a x</i>  <i>x</i>   <i>_{b x}</i>₎₃ 2 _ _{4 6}<i>_x</i> _ _{4 0}_

a) C¸c hƯ sè : a = 3 ; b = 8 => b’ = 4 ; c = 4
Gi¶i

2 2

' <i>b</i>' <i>ac</i> 4 3.4 4 0

       _; ' 2
Ph ơng trình có 2 nghiệm phân biÖt

1

' ' 4 2 2

;
3 3
<i>b</i>
<i>x</i>
<i>a</i>
     

   ₂ ' ' 4 2 2

3

<i>b</i>
<i>x</i>
<i>a</i>
    
  

b) C¸c hƯ sè : a = 3 ; b

= ; c = - 4

4 6 <i>b</i>' 2 6

  

2 2

' <i>b</i>' <i>ac</i> ( 2 6) 3.( 4) 24 12 36 0

         

' 6

_{. Ph ơng trình có 2 nghiệm ph©n biƯt}

1

' ' 2 6 6

;
3

<i>b</i>
<i>x</i>
<i>a</i>
   

  1

</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

So với cách dùng công thức nghiệm để giải ph ơng trình
bậc 2 ta đã làm đầu giờ học , cách này có u điểm gì hơn
khơng ? Em hãy quan sát li li gii :

Ph ơng trình có hai nghiệm phân biệt :

* Kết luận : Ph ơng trình có hai nghiƯm ph©n biƯt
a) 3x2_{+ 8x + 4 = 0}

2

8 4.3.4 64 48 16 0;

        4

1 2

8 4 4 2 8 4 12

; 2

2.3 6 3 2.3 6

<i>x</i>     <i>x</i>    

1 2

2

; 2

3

<i>x</i>  <i>x</i>

<b>Dùng công thức nghiệm :</b>

a) Các hệ số : a = 3 ; b = 8 => b’ = 4 ; c = 4

Ph ơng trình có 2 nghiệm ph©n biƯt
* KÕt ln :

2

' 4 3.4 4 0

    

</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

2

)7 6 2 2 0

<i>c x</i>  <i>x</i>  

2

' ( 3 2) 7.2 18 14 4 0;

      ' 2

Ph ơng trình có 2 nghiệm ph©n biƯt :
1

3 2 2
7

<i>x</i>   2

3 2 2
7

<i>x</i>

Trong bài tập khi nào ta nên
dùng công thøc nghiƯm thu

gän ?

</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

Nh ng kh«ng phải cứ giải ph ơng
trình bậc hai là ta dùng công thức
nghiệm hoặc công thức nghiệm thu
gọn đâu nhé !!!

<b>Nên giải bằng cách nào ???</b>

a) 3x2 _{+ 2x = 0}

b) - 5x2 _{- 10 = 0}

c)

d)

2 ₆ 1 ₀

2

<i>x</i>  <i>x</i>

2

</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>

<b>Bài tập 19( SGK/Trg49)</b>

Đố em biết vì sao khi a > 0 và ph ơng trình ax2_{+ bx + c = 0 vô}

nghiệm thì ax2_{+ bx + c > 0 với mọi x.}

<i><b>Đố ?</b></i>

<b>Gợi ý: </b>

Khi nào ph ơng trình ax2_{+ bx + c = 0 vô nghiệm ?}

V
ớ
i
a
>
0
v
à
t
h
ì
a
x
2
+
b
x
+
c
>
0
v
ớ
i
m
ọ
i
x
n

g
h
ĩ
a
l
à
t
a
m
t
h
ứ
c
b
ậ
c
h
a
i
đ
ó
c
ó
g
i
á
t
r
ị
n

h
ỏ
n
h
ấ
t
l
à
1
s
ố
d
ơ
n
g
.

Bài toán quy về tìm GTNN của một đa thức

</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13>

<b>Bài tập 19( SGK/Trg49)</b>

<i><b>Đố ?</b></i>

Đố em biết vì sao khi a > 0 và ph ơng trình ax2_{+ bx + c = 0 vô}

nghiệm thì ax2_{+ bx + c > 0 víi mäi x.}

<b>Gi¶i : </b>

Ta cã: ax2_{+ bx + c =} <i>a x</i>( 2 <i>b</i> <i>x</i> <i>c</i> )

<i>a</i> <i>a</i>

 

2 2

2

2 2

( 2 )

2 4 4

<i>b</i> <i>b</i> <i>b</i> <i>c</i>

<i>a x</i> <i>x</i>

<i>a</i> <i>a</i> <i>a</i> <i>a</i>

     2 2

2
4

( )

2 4

<i>b</i> <i>b</i> <i>ac</i>

<i>a x</i>
<i>a</i> <i>a</i>
  
 _   _
 
2
2 4
( )
2 4

<i>b</i> <i>b</i> <i>ac</i>

<i>a x</i>

<i>a</i> <i>a</i>



  

ph ¬ng trình ax2_{+ bx + c = 0 vô nghiệm}
2

2 4

0 4 0 0

4

<i>b</i> <i>ac</i>

<i>b</i> <i>ac</i>

<i>a</i>


        _{( do a > 0 )}

2 ₄
0
4
<i>b</i> <i>ac</i>
<i>a</i>

  
2
2 4

( ) 0

2 4

<i>b</i> <i>b</i> <i>ac</i>

<i>a x</i>

<i>a</i> <i>a</i>



</div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>

<b>CHÚC</b>

<b> CÁC </b>

<b>EM </b>

<b>HỌC </b>

<b>TỐT</b>

<b>H ớng dẫn về nhà: </b><i><b>( Chuẩn bị cho giờ học sau )</b></i>

Học thuộc các công thức nghiệm,

</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15></div>

<!--links-->