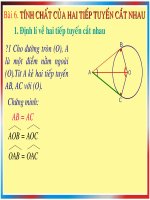<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>

<b>Líp 9d</b>

</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

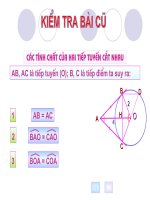
<b>KiĨm tra bµi cị.</b>

- Phát biểu định lí về dấu hiệu nhận biết tiếp

tuyến của đ ờng trịn?

</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

<b>KiĨm tra bµi cị.</b>

- Nếu một đ ờng thẳng đi qua một điểm của đ

ờng trịn và vng góc với bán kính đi qua

điểm đó thì đ ờng thẳng ấy là một tiếp tuyn

ca ng trũn.

Trả lời:

d

</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

ã Trên hình vẽ ta có AB và AC là hai tiếp

tuyến tại B và tại C của đường trịn (O).

A

B

C

O

Em có nhận xét gì về quan h của AB và AC đối với

ệ

đường tròn(O) ?

</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

<b>1. Định lí về hai tiếp tuyến cắt </b>

<b>nhau.</b>

<b>?1</b>

Cho hình 79 trong đó AB,

AC theo thø tự là các tiếp tuyến

t¹i B, t¹i C cđa ® êng trßn (O).

H·y kĨ tên một vài đoạn thẳng

bằng nhau, mét vµi gãc b»ng

nhau trong h×nh?

A

O

B

C

OB = OC =R

AB = AC

BAO = CAO

ABO = ACO = 90

0

BOA = COA

<i><b>TIẾT 28</b></i>

<b>: </b>

§

<b>6 TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU</b>

Chøng minh đ ợc:

</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

<b>1. Định lí về hai tiếp tuyến cắt </b>

<b>nhau.</b>

A

O

B

C

<i><b>TIT 28</b></i>

<b>: </b>

Đ

<b>6 TNH CHT CA HAI TIP TUYN CT NHAU</b>

Định lí:

Nếu hai tiÕp

tuyÕn

cña mét đ ờng tròn cắt nhau

tại một ®iĨm th×:

<i> - Điểm đó cách đều hai tiếp </i>

<i>điểm.</i>

<i> -Tia kẻ từ điểm đó đi qua </i>

<i>tâm là tia phân giác của góc </i>

<i>tạo bởi hai tiếp tuyến.</i>

<i> - Tia kẻ từ tâm đi qua điểm </i>

<i>đó là tia phân giác của góc </i>

<i>tạo bởi hai bán kính đi qua </i>

<i>các tiếp điểm.</i>

GT

KL

AB vµ AC lµ hai tiếp

tuyến của đ ờng tròn (O)

tại B và C.

</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

Ta

cã AB BO; AC CO (t/c tiÕp tuyÕn)

=> ABO = ACO = 90

0

XÐt



AOB vµ



AOC cã:

ABO = ACO = 90

0

OB = OC ( = R)

OA là cạnh chung

Vậy

AOB =

AOC (Cạnh huyền- cạnh góc vuông)

Suy ra: AB = AC

BAO = CAO

BOA = COA

nên AO là tia phân giác của BAC

nên OA là tia phân giác của BOC

A

O

B

C

</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

c) MO laø tia phân giác c a

ủ

góc

AMB

Chọn khẳng định sai:

a) MA = MB

Cho hỡnh veừ sau:

<b>Baứi taọp </b>

M

A

B

O

H

b)

OM là đ ờng trung trực của AB.

</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

?2.

<b>Thc phõn giỏc</b>

Tõm

HÃy nêu cách tìm tâm của một miếng gỗ

hình tròn bằng th ớc phân giác ?

- Đặt miếng gỗ hình tròn tiếp

xúc với hai cạnh của th ớc.

- Kẻ theo tia phân giác của th

ớc, ta vẽ ® ỵc mét ® êng kÝnh

cđa hình tròn.

-Xoay miếng gỗ rồi làm tiÕp

tơc nh trªn, ta vẽ đ ợc đ ờng

kính thứ hai.

</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

A

B

C

<b>I</b>

D

E

F

?3. Cho tam giác ABC. Gọi I là giao điểm của các đ
ờng phân giác các góc trong của tam giác; D, E, F theo
thứ tự là chân các đ ờng vng góc kẻ từ I đến các cạnh
BC, AC, AB. Chứng minh rằng ba điểm D, E, F cùng
nằm trên một đ ờng trịn tâm I.

<i><b>TIẾT 28</b></i>

<b>: </b>

§

<b>6 TÍNH CHẤT CA HAI TIP TUYN CT NHAU</b>

<b>2. Đ ờng tròn nội tiÕp tam gi¸c</b>

Muèn chøng minh D, E, F cïng n»m trên đ ờng

tròn tâm I ta phải chứng minh những đoạn thẳng

nào bằng nhau?

</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

A

B

C

<b>I</b>

D

E

F

Em cú nhận xét gì về vị trí của đường trịn (I;ID)

đối với ba cạnh của tam giác ABC ?

?3. Cho tam giác ABC. Gọi I là giao điểm của các đ
ờng phân giác các góc trong của tam giác; D, E, F theo
thứ tự là chân các đ ờng vng góc kẻ từ I đến các cạnh
BC, AC, AB. Chứng minh rằng ba điểm D, E, F cùng
nằm trên một đ ờng trịn tâm I.

V× I thuộc phân giác góc A nên IE = IF (1)

Vì I thuộc phân giác góc B nên IF = ID (2)

Tõ (1) vµ (2)=> IE = IF = ID

=> D, E, F cïng

n»m trên một đ ờng

tròn (I; ID).

<i><b>TIT 28</b></i>

<b>: </b>

§

<b>6 TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU</b>

<b>2. Đ ờng tròn nội tiếp tam giác</b>

</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>

<i><b>Đường tròn tiếp xúc với ba cạnh của tam giác </b></i>

<i><b>gọi là</b></i>

<i><b>đường trịn nội tiếp tam giác.</b></i>

<i><b>Khi đó tam </b></i>

<i><b>giác được gọi là</b></i>

<i><b>tam giác ngoại tiếp đường tròn</b></i>

<i><b> </b></i>

<i><b> </b></i>

Tâm của đường tròn

nội tiếp tam giác là

giao điểm của ba

đường phân giác trong

của tam giác đó

E

A

B

_C

<b>I</b>

D

F

</div>
<span class='text_page_counter'>(13)</span><div class='page_container' data-page=13>















<b>A</b>

<b>B</b>

<b>C</b>

<b>BÁN KÍNH (R)</b>

<b>TÂM (O)</b>

<b>O</b>

</div>
<span class='text_page_counter'>(14)</span><div class='page_container' data-page=14>

<b>?4. Cho tam giác ABC, K là giao điểm các đ ờng phân giác của hai góc ngồi tại B và C; D, </b>
<b>E, F theo thứ tự là chân các đ ờng vng góc kẻ từ K đến các đ ờng thẳng BC, AC, AB. </b>
<b>Chứng minh rằng ba điểm D, E, F nằm trên cùng một đ ờng trịn có tâm K.</b>

A

B

C

<b>K</b>

F

E

<b>D</b>

3 . Đường trịn bàng tiếp tam giác

<i><b>TIẾT 28</b></i>

<b>: </b>

§

<b>6 TÍNH CHẤT CỦA HAI TIẾP TUYN CT NHAU</b>

K thuộc tia phân giác của góc CBF nên KD = KF.

K thuộc tia phân giác của góc BCE nªn KD = KE.



_{KD = KE = KF.}

VËy D, E, F cùng nằm trên cùng một đ ờng tròn (K; KD).

</div>
<span class='text_page_counter'>(15)</span><div class='page_container' data-page=15>

• Đường trịn tiếp xúc với một cạnh của tam

giác và tiếp xúc với các phần kéo dài của hai

cạnh kia gọi là

<i><b>đường tròn bàng tiếp tam giác. </b></i>

Tâm của đường tròn bàng

tiếp tam giác là giao

điểm của hai đường phân

giác ngoài của tam giác.

A

F

B

C

<b>K</b>

E

<b>D</b>

</div>
<span class='text_page_counter'>(16)</span><div class='page_container' data-page=16>

<i>Với một tam giác cho trước ta vẽ được mấy </i>

<i>đường trịn bàng tiếp với tam giác đó ?</i>

A

B C

I

J

K

</div>
<span class='text_page_counter'>(17)</span><div class='page_container' data-page=17>



<b>_O</b>

<b>B</b>

<b>A</b>

<b>C</b>

<b>TÂM O</b>

<b>BÁN KÍNH R</b>

</div>
<span class='text_page_counter'>(18)</span><div class='page_container' data-page=18>

.

O

A

B

C

1.

Định lí về hai tiếp tuyến cắt nhau

2. Đường tròn nội tiếp tam giác

K

A

B

_C

<b>I</b>

H

J

D

E

Đường tròn (I;IH) nội tiếp tam giác ABC

Tam giác ABC ngoại tiếp đường tròn (I)

3 . Đường tròn bàng tiếp tam giác

A

B

C

<b>I</b>

H

K

<b>J</b>

ng tròn (I;IK) là đường trịn bàng tiếp

Đườ

trong góc A của tam giác ABC.

Tâm I của đường trịn là giao điểm ba

phân giác trong của tam giác ABC

Tâm của đường tròn bàng tiếp trong góc A là

giao điểm của hai đường phân giác các góc

ngồi tại B và C.

<i>AB = AC</i>

<i>AB ; AC là hai tiếp tuyến của (O)</i>

( ) ;

( )

<i>B</i>



<i>O</i>

<i>C</i>



<i>O</i>

<i>Tia AO laø tia phân giác góc BAC</i>

<i>Tia OA là tia phân giác góc BOC</i>

GT

KL

</div>
<span class='text_page_counter'>(19)</span><div class='page_container' data-page=19>

5) Tâm của đường tròn bàng

tiếp tam giác

4) Tâm của đường tròn nội

tiếp tam giác

3) Đường tròn ngoại tiếp

tam giác

2) Đường tròn bàng tiếp tam

giác

1) Đường tròn nội tiếp tam

giác

a) là đường tròn đi qua ba đỉnh

_{của tam giác}

b) là đường tròn tiếp xúc với ba

cạnh của tam giác

c) là giao điểm ba đường phân giác

trong của tam giác

d) là đường tròn tiếp xúc với một cạnh

của tam giác và phần kéo dài của hai

cạnh kia

e)

là giao điểm hai đường phân giác

ngồi của tam giác

1.Nối mỗi ơ ở cột trái với một ơ ở cột phải để có kết quả đúng

1 - b ; 2 - d ; 3 – a ; 4 – c ; 5 - e

</div>
<span class='text_page_counter'>(20)</span><div class='page_container' data-page=20>

BD

CA

a) CM = ………..; DM =………..

2. Cho hình vẽ sau :

AB là đường kính của (O)

AC ; CD ; BD là các tiếp

tuyến của (O) tại A ; M và B.

A

_B

C

D

M

O

x

y

Điền nội dung thích hợp vào

_{chỗ trống:}

b) …………..= CA + BD

c) OC là tia phân giaực cuỷa

goực

<b></b>

CD

d)

OD là tia phân giác của

góc

...

</div>
<span class='text_page_counter'>(21)</span><div class='page_container' data-page=21>

<b>H ớng dẫn về nhà:</b>

-

<b>_{Nắm vững các tính chất của tiếp tuyến đ}</b>

<b>ờng tròn vµ dÊu hiƯu nhËn biÕt tiÕp tun.</b>

-

<b>_{Phân biệt định nghĩa , cách xác định tâm}</b>

<b>cđa ® êng tròn ngoại tiếp, đ ờng tròn nội </b>

<b>tiếp, đ ờng tròn bàng tiếp tam gi¸c.</b>

</div>
<span class='text_page_counter'>(22)</span><div class='page_container' data-page=22></div>
<span class='text_page_counter'>(23)</span><div class='page_container' data-page=23>

I

A

B

x

C

y

VËy:

I thuộc tia phân giác của

góc xAy suy ra

IB = IC

</div>

<!--links-->