<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>

GV: Trần Xuân Liêm

<b>Tiết 59: KIỂM TRA ĐẠI SỐ CHƯƠNG IV LỚP 9</b>
I - MỤC TIÊU : Qua bài kiểm tra nhằm

- Đánh giá sự nhận thức các kiến thức trong chươngvà kỹ năng thực hành

giải toán của HS qua chương IV

- Rèn tính kỷ luật và trung thực trong học tập, kiểm tra.

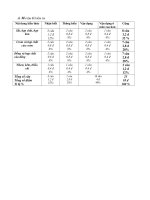
II - MA TRẬN ĐỀ

:

Mức độ

Kiến thức TNKQNhận biếtTL TNKQthông hiểuTL TNKQVận dụngTL Tổng
Hàm số y = ax2

Đồ thị hàm số y =
ax2
2
1
1
1
1
1 3,0

Phương trình bậc
hai 1 ẩn

1
0,5
1
0,5
1
1,5
1
1,5 4,0

Hệ thức Vi - ét
ứng dụng
2
1
2
1
1
1
3,0
Tổng _{5 2,5 5 4,0} _{3 3,5} 10,0
III - ĐỀ BÀI

<b>A - Trắc nghiệm : (3,0đ) </b> Chọn đáp án đúng.

<i><b>Câu 1</b></i> : Cho hàm số y = 0,5x2_{. Kết luận nào sau đây là đúng ?}

A. Hàm số trên luôn đồng biến;

B. Hàm số trên đồng biến khi x > 0 và nghịch biến khi x < 0;
C. Hàm số trên luôn nghịch biến;

D. Hàm số trên luôn đồng biến khi x < 0 và nghịch biến khi x > 0;
<b>Câu 2:</b> Cho phương trình x2 _{+ 5x}_ _{6 = 0 có tích 2 nghiệm là.}

A.  _{6 B. 6 C.} _{5 D. Khơng tìm được tích 2 nghiệm.}
<b>Câu 3:</b> Điểm thuộc đồ thị hàm số y =  2

2
1

<i>x</i> _là

A. (1; 1

2 ) B. ( 1;
1

2) C. (1; 

1

2) D. ( 2; 
1
2)
<b>Câu 4</b>: Phương trình ax2_{+ bx + c = 0 (a}__{0) có a + b + c = 0. Khi đó nghiệm của phương}

trình là:

A. x1 =  1 và x2 = 
<i>c</i>

<i>a</i> B. x1 = 1 và x2 =
<i>c</i>

<i>a</i> C. Chưa chắc có nghiệm.

<b>Câu 5</b>: Phương trình x2_{+ 2x –3 = 0 có hai nghiệm là.}

A. x=1; x = 3 B. x = 1; x =  ₃ _{C. x=} _{1; x=} ₃ _{D. x=} _{1; x = 3.}
<b>Câu 6</b>: Phương trình ax2_{+ bx + c = 0}_{(a 0)}_ _và _b2 _4ac

  

A.  0 phương trình có hai nghiệm phân biệt x₁ b ; x₂ b

2a 2a

     

  .

B.  0 phương trình vơ nghiệm.

C.  0 phương trình có nghiệm kép 1 2
b

x x .

2a



  .
D. Cả 3 câu trên đều sai.

<b>B - Tự luận: ( 7,0đ)</b>

<i><b>Bài 1: </b></i> Cho hàm số y = ax2₍_{a 0}_ ₎

</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

GV: Trần Xuân Liêm

b) Vẽ đồ thị hàm số trên với a vừa tìm được.
<i><b>Bài 2: </b></i> Nhẩm nghiệm các phương trình sau:

a) x

2



7x 6 0

 

b)  2x2 ( 2 6)x 6 0  

<i><b>Bài 3: </b></i> Cho p t bậc hai: _x2 _{2(m 2).x m}2 ₀

    (x là ẩn, m là tham số) (1)

a)

Giải phương trình với m 3 .

b) Tìm m để phương trình (1) có hai nghiệm phân biệt.

c)

Tìm m để phương trình (1) có hai nghiệm x1; x2 thỏa mãn x12x22 16.
<b>HƯỚNG DẪN CHẤM</b>

<b>A - Trắc nghiệm : (3,0đ) Chọn đáp án đúng. Mỗi ý đúng cho 0,5 đ</b>

<b>Câu</b> <b>1</b> <b>2</b> <b>3</b> <b>4</b> <b>5</b> <b>6</b>

<b>Đáp án</b> B A C B B A

<b>B - Tự luận: ( 7,0đ)</b>

<i><b>Bài 1: </b></i> Cho hàm số y = ax2₍_{a 0}_ ₎

a) Tìm a = 2 cho 1 đ

b) Lập bảng giá trị đúng cho 0,5 đ. Vẽ đồ thị hàm số đúng và đẹp cho 0,5 đ
<i><b>Bài 2: </b></i> Nhẩm nghiệm các phương trình sau:

a) x

2



7x 6 0

 

_b) _2x2 _{( 2 6)x 6 0}

    

Có a + b + c = 1 – 7 + 6 = 0 Có a – b + c =  2 2 6 6 0   cho 0,25 đ
1 1; 2 6

<i>x</i> <i>x</i>

   1 2
6
1;

2

<i>x</i> <i>x</i> 

   _{cho 0,5 đ}
<i><b>Bài 3: </b></i> Cho p t bậc hai: _x2 _{2(m 2).x m}2 ₀

    (x là ẩn, m là tham số) (1)

a)

Giải phương trình với m 3 đúng cho 1,5 đ

2 2

2

1 2

x 2(m 2).x m 0

x 10x 9 0 cho 0,5d
có a + b + c = 1 10 + 9 = 0

x 1; x 9 cho 1d

   

   


  

b)

Tìm m để phương trình (1) có hai nghiệm phân biệt đúng cho 1 đ

2 2

2 2

x 2(m 2).x m 0
' m 4m 4 m

' 4m 4 cho 0,5d

   

    
  

Để PT có 2 nghiệm phân biệt thì  0 hay 4m + 4 > 0  <i>m</i> 1 cho 0,5 đ

c)

Tìm m để phương trình (1) có hai nghiệm x1; x2 thỏa mãn x12x22 16. Tìm đúng m
cho 1 đ.

Theo Viét : x1 + x2 = 2m + 4; x1 – x2 = m2









2

2 2

1 2 1 2 1 2

2 ₂

2 2

2

x x 16 x x 2x x 16

2m 4 2m 16

4m 16m 16 2m 16 0

2m 16m 0 2m(m 8) 0

m 0 8 cho 1d

     

   

     

     

  Hoặc m =

</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

GV: Trần Xuân Liêm

Ngày soạn : 04/04/2010

<b>TUẦN 31</b>

<b>KIỂM TRA CHƯƠNG III HÌNH HỌC 9</b>
I<b> . Mục tiêu:</b>

- Kiến thức: Kiểm tra đánh giá về các góc với đường trịn, độ dài đường trịn, diện
tích hình trịn, tứ giác nội tiếp đường trịn…

- Kĩ năng: Rèn luyện kĩ năng trình bày, khả năng tư duy lô-gic.

II. Ma tr n thi t k

ậ

ế ế đề ể

ki m tra:

Kiến thức

Nhận biết Thông hiểu Vận dụng

Tổng

KQ TL KQ TL KQ TL

1. Góc với đường trịn 2 1 1 4

1 0,5 2 3,5

2. Tứ giác nội tiếp 1 1 2

0,5 3 3,5

3. Độ dài đường tròn 1 1 1 3

diện tích hình trịn 0,5 0,5 2 3

Tổng

4 3 2 9

2 4 4 10

<b>III. Đề kiểm tra:</b>

<b>Phần I: Trắc nghiệm khách quan(3,0 đ)</b>: Mỗi câu có 4 đáp án A; B; C; D. Em hãy
khoanh tròn đáp án đúng trong các câu sau:

<b>Câu 1 :</b> Góc nội tiếp chắn nửa đường trịn là

A. góc nhọn B. góc vng C. góc tù D. góc bẹt.
<b>Câu 2 :</b>. Tứ giác ABCD nội tiếp đường tròn có _DAB ₌₁₂₀0_{.Vậy số đo}_

BCDlà:

A . 600_{; B . 120}0_{; C . 90}0_{; D . Kết quả khác.}

<b>Câu 3 : </b>Diện tích của hình quạt trịn 1200_{của đường trịn có bán kính 3cm là:}

A .  _(cm2_{) ; B . 2}__(cm2_{) ; C . 3}_ _(cm2_{) ; D . 4}__(cm2₎

<b>Câu 4 :</b> Hai bán kính OA, OB của đường trịn tạo thành góc ở tâm là 800_{. Số đo cung lớn}

AB là

A1600_{; B. 280}0_{; C . 80}0_{; D . Một đáp số khác.}

<b>Câu 5</b>; AB là một dây cung của (O; R ) với Sđ<i>_AB</i>_{= 80}0

; M là điểm trên cung lớn AB. Góc

AMB có số đo là :
A. 2400

; B. 1600 ; C. 400 ; D. 800

<b>Câu 6 :</b> Hình trịn có diện tích 12,56 cm2_{. Vậy chu vi của đường tròn là :}

A. 25,12cm ; B. 12,56 cm ; C . 6,28 cm ; D . 3,14 cm
<b>B/ Tự luận : (</b>7điểm)

</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

GV: Trần Xuân Liêm

a. Chứng minh: Tứ giác AFHE, tứ giác BFEC nội tiếp.

b.

Hai đường thẳng BE và CF cắt (O) tại P và Q. Chứng minh: sđAQ = sđ_AP
c. Cho biết sđ_AB _{= 90}0_{, bán kính R = 10cm. Tính chu vi hình viên phân giới}

hạn bởi dây AB và cung nhỏ AB.

<b>HƯỚNG DẪN CHẤM</b>

<b>A - Trắc nghiệm : (3,0đ) Chọn đáp án đúng. Mỗi ý đúng cho 0,5 đ</b>

<b>Câu</b> <b>1</b> <b>2</b> <b>3</b> <b>4</b> <b>5</b> <b>6</b>

<b>Đáp án</b> B A C B C B

<b>B - Tự luận: ( 7,0đ)</b>

<i><b> </b></i>Cho tam giác ABC có 3 góc nhọn nội tiếp đường trịn (O; R). Hai đường cao BE và CF
cắt tại H.

a.

Chứng minh đúng Tứ giác AFHE, tứ giác BFEC nội tiếp. Mỗi ý đúng cho 1,5 đ

b.

Chứng minh được sđAQ = sđ_AP _{cho 2 đ}

c. Tính đúng chu vi hình viên phân giới hạn bởi dây AB và cung nhỏ AB cho 1,5 đ
(Vẽ hình đúng cho 0,5 đ)

A

B C

E
F

H

P

</div>

<!--links-->