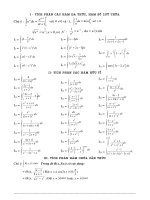chuyen de nguyen ham
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (153.51 KB, 4 trang )
<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>
<i><b>Chuyên đề: Nguyên hàm – Tích phân </b></i><b>Nguyễn Tiên Phong</b>
<b>Mục lục</b>
<b>§1. Nguyên hàm</b>
<b>- Định nghĩa</b>
<b>- Tính chất</b>
<b>- Bảng nguyên hàm</b>
<b>- Phương pháp đơn giản tính ngun hàm.</b>
<b>§2. Tích phân</b>
<b>- Định nghĩa và ý nghĩa</b>
<b>- Tính chất</b>
<b>- Phương pháp tính: Phân tích, đổi biến, tích phân từng phần, liên kết.</b>
<b>- Một số dạng tích phân đặc biệt</b>
<b>§3. Tích phân của một số lớp hàm cơ bản.</b>
<b>- Tích phân của hàm số hữu tỉ.</b>
<b>- Tích phân của hàm số lượng giác</b>
<b>- Tích phân của hàm số vơ tỉ.</b>
<b>§4. Ứng dụng của tích phân</b>
<b>- Tính diện tích hình phẳng</b>
<b>- Tính thể tích vật trịn xoay sinh bởi miền hình phẳng quay quanh trục Ox, Oy.</b>
</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>
<i><b>Chuyên đề: Nguyên hàm – Tích phân </b></i><b>Nguyễn Tiên Phong</b>
<b>§1. Nguyên hàm</b>
<b>1. Định nghĩa:</b>
Hàm số <i>F x</i>( )gọi là một nguyên hàm của hàm số <i>f x</i>( ) trên khoảng ( ; )<i>a b</i> nếu với <i>x</i> ( ; )<i>a b</i> ta có:
'( ) ( )
<i>F x</i> <i>f x</i> .
Nếu thay cho ( ; )<i>a b</i> bằng
<i>a b</i>;
thì phải có thêm: <i>F a</i>'( ) <i>f a</i>( ); '( )<i>F b</i> <i>f b</i>( ) .
Ví dụ: 1) <i>f x</i>( ) 2 <i>x</i>có nguyên hàm là <i><sub>F x</sub></i><sub>( )</sub> <i><sub>x</sub></i>2
2) <i>F x</i>( ) tg <i>x</i> là nguyên hàm của ( ) 1<sub>2</sub>
cos
<i>f x</i>
<i>x</i>
3) <i>f x</i>( ) sin <i>x</i> có nguyên hàm là <i>F x</i>( ) cos<i>x</i>
<b>2. Định lý:</b>
Nếu <i>F x</i>( ) là một nguyên hàm của hàm số <i>f x</i>( ) trên khoảng ( ; )<i>a b</i> thì:
<i>- Với mọi hằng số C, F x</i>( )<i>C</i> cũng là 1 nguyên hàm của <i>f x</i>( )
- Ngược lại, mọi nguyên hàm của <i>f x</i>( ) trên khoảng ( ; )<i>a b</i> đều có dạng <i>F x</i>( )<i>C</i>.
Tất cả các nguyên hàm của <i>f x</i>( ) trên khoảng ( ; )<i>a b</i> gọi là 1 họ nguyên hàm của <i>f x</i>( ), ký hiệu là
<sub></sub>
<i>f x dx</i>( ) .Vậy:
<b>3. Tính chất:</b>
1)
'
( ) ( )
<i>f x dx</i> <i>f x</i>
2)<sub></sub>
<i>af x dx a</i>( ) <sub></sub>
<i>f x dx</i>( ) 3)<sub></sub>
<i>f x</i>( )<i>g x dx</i>( )
<sub></sub>
<i>f x dx</i>( ) <sub></sub>
<i>g x dx</i>( )4) Nếu
<sub></sub>
<i>f t dt F t</i>( ) ( )<i>C</i> thì<sub></sub>
<i>f u du F u</i>( ) ( )<i>C u u x</i>, ( ).<b>4. Bảng các nguyên hàm:</b>
<b>Nguyên hàm cơ bản</b> <b>Nguyên hàm của hàm số hợp</b>
<i>1) dx x C</i>
<sub></sub>
<sub></sub>
<i>du u C</i> 2)
1
, 1
1
<i>x</i>
<i>x dx</i> <i>C</i>
1
, 1
1
<i>u</i>
<i>u du</i> <i>C</i>
2
2
3) ln
4)
5) ,0 1
ln
6) cos sin
7) sin cos
8) tg
cos
9) cotg
sin
<i>x</i> <i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x C</i>
<i>x</i>
<i>e dx e</i> <i>C</i>
<i>a</i>
<i>a dx</i> <i>C</i> <i>a</i>
<i>a</i>
<i>xdx</i> <i>x C</i>
<i>xdx</i> <i>x C</i>
<i>dx</i>
<i>x C</i>
<i>x</i>
<i>dx</i>
<i>x C</i>
<i>x</i>
2
2
3) ln
4)
5) ,0 1
ln
6) cos sin
7) sin cos
8) tg
cos
9) cotg
sin
<i>u</i> <i>u</i>
<i>u</i>
<i>u</i>
<i>du</i>
<i>u C</i>
<i>u</i>
<i>e du e</i> <i>C</i>
<i>a</i>
<i>a du</i> <i>C</i> <i>a</i>
<i>a</i>
<i>udu</i> <i>u C</i>
<i>udu</i> <i>u C</i>
<i>du</i>
<i>u C</i>
<i>u</i>
<i>du</i>
<i>u C</i>
<i>u</i>
<b>5. Ví dụ: Các VD sau sử dụng các tính chất của nguyên hàm và nguyên hàm của hàm số hợp.</b>
<i><b>Trang 2</b></i>
( ) ( )
<i>f x dx F x</i> <i>C</i>
</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>
<i><b>Chuyên đề: Nguyên hàm – Tích phân </b></i><b>Nguyễn Tiên Phong</b>
1)
<sub></sub>
<i>x</i> <i>x</i> <i>dx</i><i>x</i> <i>x</i> 2<i>x</i><i>C</i>2
5
)
2
5
3
(
2
3
2 <sub>2) </sub>
<i>dx</i> <i>x</i> <i>x</i> <i>C</i>
<i>x</i>
<i>x</i> 2 2 2ln
4 2
3)
<sub></sub>
(2<i>ex</i> 5cos<i>x</i>)<i>dx</i>2<i>ex</i> 5sin<i>x</i><i>C</i> 4) <i>dx</i> <i>x</i> <i>x</i> <i>C</i><i>x</i>
<i>x</i>
4sin <sub>cos</sub>32 4cos 3tg5)
<sub></sub>
<sub></sub>
<i>C</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i> <sub>2</sub> <sub>2</sub>
5
2
3
1
3 2 5 3
1
2
1
2
3
2
6)
<sub></sub>
<sub></sub>
<i>x</i> <i>x</i> <i>C</i>
<i>x</i>
<i>d</i>
<i>x</i>
<i>dx</i>
1
2
ln
2
1
1
2
)
1
2
(
2
1
1
2
7)
<sub></sub>
<sub></sub>
<i>C</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
1
ln
1
1
1
2
1
2
3
2 2 2
8)
<sub></sub>
<i>x</i> <i>dx</i><sub></sub>
<i>x</i> <i>d</i> <i>x</i> sin(3<i>x</i>1)<i>C</i>3
1
)
1
3
(
)
1
3
cos(
3
1
)
1
3
cos(
9)
<sub></sub>
<i>x</i> <i>x</i> <i>dx</i><sub></sub>
<i>x</i> <i>d</i> <i>x</i> cos(2<i>x</i> 1)<i>C</i>4
1
)
1
2
(
)
1
2
sin(
4
1
)
1
2
sin( 2 2 2 2
10)
<sub></sub>
<i>x</i> 7<i>dx</i><sub></sub>
<i>x</i> 7<i>d</i> <i>x</i> (5<i>x</i>3)8<i>C</i>40
1
)
3
5
(
)
3
5
(
5
1
)
3
5
(
11)
<sub></sub>
<sub></sub>
<i>x</i><i>C</i><i>x</i>
<i>x</i>
<i>d</i>
<i>x</i>
<i>dx</i>
3
tg
3
1
3
cos
)
3
(
3
1
3
cos2 2
12)
<sub></sub>
<i>x</i> <i>xdx</i><sub></sub>
<i>xd</i> <i>x</i> <i>x</i><i>C</i>4
sin
)
(sin
sin
cos
sin
4
3
3
13)
<sub></sub>
<sub></sub>
<i><sub>dx</sub></i> <i><sub>d</sub></i> <i><sub>x</sub></i> <i><sub>C</sub></i>
<i>x</i> <i>x</i> <i>x</i> <i>x</i>
2
ln
2
2
)
1
(
2
2
1
2
. 1 1 2 1
2
2
2
14)
<sub></sub>
<i>x</i> <i>dx</i><sub></sub>
<i>x</i> 2<i>d</i> <i>x</i> <i>x</i> 3 <i>C</i>1
)
5
3
(
9
2
)
5
3
(
)
5
3
(
3
1
5
3
<b>Bài tập: Tìm các nguyên hàm sau.</b>
<sub></sub> <sub></sub> <sub></sub>
1
1
I
5
2
)
1
2
(
I
cos
sin
sin
I
I1 2 3 4 4
<i>x</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>tgxdx</i>
</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>
<i><b>Chuyên đề: Nguyên hàm – Tích phân </b></i><b>Nguyễn Tiên Phong</b>
<i>x</i>
<i>xdx</i>
<i>e</i>
<i>e</i>
<i>dx</i>
<i>e</i>
<i>dx</i>
<i>e</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>e</i>
<i>dx</i>
<i>e</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>a</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>b</i>
<i>x</i>
<i>a</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>xdx</i>
<i>a</i>
<i>a</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>xdx</i>
<i>x</i>
<i>xdx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>xdx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>x</i>
<i>dx</i>
<i>dx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>xdx</i>
<i>x</i>
<i>x</i>
<i>dx</i>
<i>xdx</i>
<i>xdx</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
<i>x</i>
sin
1
cos
I
1
)
1
(
I
1
I
)
1
3
(
)
1
2
(
I
)
1
(
)
2
3
(
I
)
4
11
(
I
)
1
(
9
3
2
I
1
5
3
I
2
I
)
1
(
I
)
5
1
(
I
5
2
I
)
1
(
I
)
ln(ln
ln
I
1
1
2
I
9
I
1
I
1
I
1
I
)
2
)(
1
(
I
2
I
4
I
9
I
I
1
3
)
3
4
(
I
3
1
I
cos
sin
cos
sin
I
cos
sin
cos
sin
I
2
cos
sin
I
)
0
(
I
cos
sin
cos
sin
I
cos
sin
I
sin
cos
I
cos
sin
I
cos
sin
I
)
tg
(sin
I
tg
I
cos
I
cos
1
I
2
cos
1
I
cos
sin
cos
sin
I
2
sin
1
I
3
cos
sin
I
cos
I
sin
I
cos
I
5
50
49
48
5 4
2
47
5 2
2
46
5 3
45
10
2
44
2
43
5
42
100
2
41
10
2
3
40
39
10
38
37
2
36
3
2
35
2
34
33
32
2
2
31
2
30
8
3
29
2
28
2
2
27
3
26
3
25
2
2
2
2
24
3
23
22
2
2
21
20
2
3
19
3
18
2
17
16
2
15
2
14
13
12
11
2
2
10
9
8
4
7
3
6
2
5
<b>§1. Tích phân</b>
1. Định nghĩa:
Cho hàm số <i>f x</i>( ) liên tục và có nguyên hàm <i>F x</i>( ) trên đoạn
<i>a b</i>;
<i>.Tích phân từ a đến b của hàm số </i> <i>f x</i>( ) là<b>1số, ký hiệu </b> <i>b</i> ( )
<i>a</i> <i>f x dx</i>
,tính theo cơng thức:Ví dụ: 1)
1
3
1 2
0
0
1
3 3
<i>x</i>
<i>x dx </i>
2) 2 20
0 cos<i>xdx</i> sin<i>x</i> sin <sub>2</sub> sin 0 1
3) 1 1 1 0
0 0 1
<i>x</i> <i>x</i>
<i>e dx e</i> <i>e</i> <i>e</i> <i>e</i>
<i><b>Trang 4</b></i>
( ) ( ) ( ) ( )
<i>b</i> <i><sub>b</sub></i>
<i>a</i>
<i>a</i> <i>f x dx F x</i> <i>F b</i> <i>F a</i>
</div>
<!--links-->