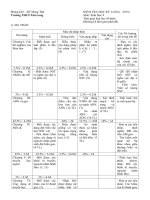
Đề thi khảo sát môn: Sinh học 9 - Trường THCS Lê Quý Đôn
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (137.74 KB, 2 trang )
<span class='text_page_counter'>(1)</span>TƯƠNG GIAO CỦA HAI ĐỒ THỊ Cho 2 đường: (C1) : y = f(x) và (C2) : y = g(x). Pt hoành độ giao điểm của hai đường là : f(x) = g(x) (*) Số nghiệm của Pt (*) là số giao điiểm của hai đường (C1) & (C2). f ( x) g ( x) có nghiệm f '( x) g '( x). Điều kiện tiếp xúc: để (C1) tiếp xúc (C2), điều kiện là hệ Pt : * BÀI TẬP: (42) Cho (C) : y = x 4 - 5x 2 + 4 a) Khảo sát và vẽ đồ thị (C) của hs. b) Tìm m để (C) tiếp xúc với (P) : y = x 2 + m . Tìm tọa độ các tiếp điểm (43) Cho (C) : y = x 4 - (m 2 + 10)x 2 + 9 a) Khảo sát và vẽ đồ thị (C) của hs với m = 0 b) CMR với m 0, đồ thị luôn cắt Ox tại 4 điểm phân biệt. Trong các giao điểm đó có hai điểm nằm trong khoảng (-3 ; 3) và có hai điểm nằm ngoài khoảng (-3 ; 3) (44) Cho (C m ) : y = 2x 3 + 3(m – 3)x 2 + 11 – 3m a) Tìm pt các đường thẳng qua A(. 19 ; 4) và tiếp xúc với đồ thị (C 2 ) của hs 12. b) Tìm m để (C m ) có 2 cực trị, đồng thời các điểm cực trị M 1 ; M 2 và B(0 ; -1) thẳng hàng (45) Cho (C) : y = 2x 3 - x 2 a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm m để (d): y = m cắt (C) tại ba điểm có hoành độ x 1 ; x 2 ; x 3 . Tính tổng: x12 x22 x32 ? (46) Cho (C) : y =. 2x 1 x 1. a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm m để đường thẳng (d): y = mx + 2m - 1 cắt (C) tại hai điểm trên cùng một nhánh. (47) Cho hs : y =. x +1 x -1. a) Khảo sát và vẽ đồ thị (C) của hs b) CMR đường thẳng (d): 2x – y + m = 0 luôn cắt (C) tại hai điểm phân biệt A, B trên 2 nhánh của (C) c) Tìm m để đoạn AB ngắn nhất (48) Cho (C) : y =. 2 x 1 x 1. a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm m để đường thẳng (d): y = – x + 3m cắt (C) tại hai điểm A, B sao cho AB = 2 2 . Tìm tọa độ của A ; B (49) Cho (C) : y =. 2x 1 x2. Lop12.net.
<span class='text_page_counter'>(2)</span> a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm m để đường thẳng (d): y = mx – m + 5 cắt (C) tại hai điểm phân biệt A(x 1 ;y 1 ), B(x 2 ;y 2 ). Tìm hệ thức giữa x 1 ; x 2 độc lập với m (50) Cho hàm số y . x2 2x 4 x2. a) Khảo sát và vẽ đồ thị (C) của hàm số. b) Tìm m để đường thẳng dm: y = mx + 2 – 2m cắt đồ thị (C) tại hai điểm phân biệt. (51) Cho (C) : y =. x2 x m xm. a) Tìm m để tiệm cận xiên đi qua điểm M(2 ;0). Khảo sát và vẽ đồ thị (C) của hs với m tìm được. b) Tìm m để đường thẳng y = x – 1 luôn cắt (C) tại 2 điểm phân biệt A(x 1 ;y 1 ), B(x 2 ;y 2 ). Tìm hệ thức giữa y 1 ; y 2 không phụ thuộc vào m (52) Cho (C) : y =. x2 x 2 x2. a) Khảo sát và vẽ đồ thị (C) của hs b) Gọi A là điểm cực đại của (C). Tìm m để đường thẳng (d) : x + 2y – 2m = 0 cắt (C) tại hai điểm B ; C sao cho ABC vuông ở A. (53) Cho (C) : y =. x2 2x 3 x2. a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm trên (C) hai điểm A ; B sao cho đường thẳng AB cùng phương với y = - x ; đồng thời độ dài AB ngắn nhất (54) Cho (C) : y =. 2x2 2x 1 2x 1. a) Khảo sát và vẽ đồ thị (C) của hs b) Tìm m để đường thẳng y = m cắt (C) tại 2 điểm phân biệt A ; B sao cho OAB có diện tích bằng. 10 (đvdt) 9. Lop12.net.
<span class='text_page_counter'>(3)</span>
![Đề Thi Thử ĐH Môn TOÁN Lần I - THPT Chuyên Lê Quý Đôn [2009 - 2010] pptx](https://media.store123doc.com/images/document/2014_07/02/medium_mad1404310817.jpg)
