ĐÁNH GIÁ TÍNH ổn ĐỊNH của hệ THỐNG (PHẦN 1) (cơ sở tự ĐỘNG SLIDE)
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (428.87 KB, 33 trang )
CHƯƠNG 4
ĐÁNH GIÁ TÍNH ỔN ĐỊNH
CỦA HỆ THỐNG
Nội dung chương 4
4.1 Khái niệm ổn định
4.2 Các tiêu chuẩn ổn định đại số
Điều kiện cần
Tiêu chuẩn Routh
Tiêu chuẩn Hurwitz
4.3 Phương pháp quỹ đạo nghiệm số (QĐNS)
Khái niệm QĐNS
Phương pháp vẽ QĐNS
Xét tính ổn định dùng QĐNS
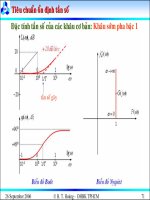
4.4 Tiêu chuẩn ổn định tần số
Khái niệm đặc tính tần số
Đặc tính tần số của các khâu cơ bản
Đặc tính tần số của hệ thống tự động
Khái niệm ổn định
Xét ví dụ
Khái niệm ổn định
Ví dụ
Khái niệm ổn định
Định nghĩa ổn định BIBO
Hệ thống được gọi là ổn định BIBO (Bounded Input Bounded Output)
nếu ngõ ra hệ thống bị chặn khi ngõ vào bị chặn.
Khái niệm ổn định
Cực và Zero
Xét hệ thống có hàm truyền sau
b 0s m + b1s m −1 + L + b m −1s + b m
G(s) =
a 0s n + a1s n −1 + L + a n −1s + a n
Đặt
B(s) = b 0s m + b1s m −1 + L + b m −1s + b m
A(s) = a 0s n + a1s n −1 + L + a n −1s + a n
Zero là nghiệm của pt B(s) = 0. Ký hiệu: zi (i=1÷m)
Cực là nghiệm của pt A(s) = 0. Ký hiệu: pi (i=1÷n)
Khái niệm ổn định
Giản đồ Cực - Zero
Giản đồ Cực – Zero là đồ thị biểu diễn vị trí các cực và zero của hệ
thống trên mặt phẳng phức.
Im
Zero
Cực
Re
Khái niệm ổn định
Điều kiện ổn định
Tính ổn định của hệ thống phụ thuộc vị trí các cực
Hệ thống có tất cả các cực với phần thực âm (tất cả các cực ở bên
trái mp phức): hệ thống ổn định
Hệ thống có cực với phần thực bằng 0, các cực cịn lại có phần thực
âm: hệ thống ở biên giới ổn định
Hệ thống có ít nhất một cực với phần thực dương (ít nhất một cực
ở bên phải mp phức) : hệ thống không ổn định
Khái niệm ổn định
Ví dụ
Xác định sự ổn định của hệ thống có các cực như sau:
a)
b)
c)
-1, -2
e) -2 + j, -2 - j, 2j, -2j
-1, +1
f) 2,-1,-3
-3,-2,0
g) -6,-4,7
d) -1 + j, -1- j
h) -2 + 3j, -2 -3j, -2
Khái niệm ổn định
Ví dụ
Khái niệm ổn định
Phương trình đặc trưng
Phương trình đặc trưng : A(s) = 0
Đa thức đặc trưng : A(s)
R(s)
C(s)
+
G(s)
-
& = Ax(t) + Bu(t)
x(t)
y(t) = Cx(t) + Du(t)
H(s)
Phương trình đặc trưng
1 + G(s)H(s) = 0
Phương trình đặc trưng
det(Is − A) = 0
Tiêu chuẩn ổn định đại số
Điều kiện cần
Điều kiện cần để hệ thống ổn định là tất cả các hệ số của PTĐT
phải khác 0 và cùng dấu.
Ví dụ hệ thống có PTĐT
s3 + 2s2 + 5s - 1 = 0 :
s4 + 3s2 + 6s + 1 = 0 :
s3 + s2 + 4s + 7 = 0 :
Không ổn định
Không ổn định
Chưa kết luận
Tiêu chuẩn ổn định Routh
Quy tắc lập bảng Routh
Cho hệ thống có PTĐT sau
n
n −1
a 0s + a1s + L + a n −1s + a n = 0
s
s
n
c11 = a0
c12 = a2
c13 = a4
…
n-1
c21 = a1
c22 = a3
c23 = a5
…
n-2
c31 = c12 – α3c22
c32 = c13 – α3c23
c33 = c14 – α3c24
…
n-3
c41 = c22 – α4c32
c42 = c23 – α4c33
c43 = c24 – α4c44
…
…
…
…
…
α3= c11/c21
s
α4= c21/c31
s
…
…
αn =
cn-2,1/cn-1,1
s
0
cn1 =
cn-2,2 – αncn-1,2
Tiêu chuẩn ổn định Routh
Điều kiện cần và đủ để hệ thống ổn định là tất cả các
phần tử ở cột 1 bảng Routh phải cùng dấu.
Số lần đổi dấu của các phần tử ở cột 1 bảng Routh
bằng số nghiệm không ổn định của PTĐT.
Tiêu chuẩn ổn định Routh
Ví dụ 1
Cho hệ thống có PTĐT sau
s + s + 4s + 7 = 0
3
s
s
α3= 1
s
α4= -1/3
s
3
2
1
0
2
1
4
1
7
-3
0
7
Hệ thống khơng ổn định, có 2 cực ở nửa phải mp phức
Tiêu chuẩn ổn định Routh
Ví dụ 1
G = tf([1],[1 1 4 7]); pzmap(G); step(G)
Giản đồ cực zero
Đáp ứng nấc
Tiêu chuẩn ổn định Routh
Ví dụ 2
Cho hệ thống có PTĐT sau
s + 2s + 4s + 7 = 0
3
s
s
α3= 1/2
s
α4= 4
s
Hệ thống ổn định
3
2
1
0
2
1
4
2
7
0.5
0
7
Tiêu chuẩn ổn định Routh
Ví dụ 2
G = tf([1],[1 2 4 7]); pzmap(G); step(G)
Giản đồ cực zero
Đáp ứng nấc
Tiêu chuẩn ổn định Routh
Ví dụ 3
Tìm K để hệ thống vịng kín sau ổn định
R(s)
C(s)
+
G(s)
H(s)
s+2
G(s) = 3
s + 4s 2 + 5s + 3
K
H(s) =
s+2
PTĐT của hệ thống
s + 4s + 5s + 3 + K = 0
3
2
Tiêu chuẩn ổn định Routh
Ví dụ 3
s3 + 4s 2 + 5s + 3 + K = 0
s
s
α3= 1/4
s
α4= 16/(17-K)
s
3
2
1
0
1
5
4
3+K
5 – (3+K)/4
0
3+K
Điều kiện để hệ thống ổn định
5 − (3 + K) / 4 > 0
⇒ −3 < K < 17
3+ K > 0
Tiêu chuẩn ổn định Routh
Ví dụ 3
Sơ đồ Simulink
K = 10
K = 17
K = 30
Tiêu chuẩn ổn định Routh
Các trường hợp đặc biệt
Trường hợp 1
Nếu hệ số ở cột 1 của hàng nào đó của bảng Routh bằng 0, các hệ số
còn lại của hàng đó khác 0, ta thay hệ số bằng 0 ở cột 1 bởi số dương
ε nhỏ tùy ý, sau đó q trình tính tốn được tiếp tục
Tiêu chuẩn ổn định Routh
Ví dụ 4
Cho hệ thống có PTĐT sau
s + 2s + 2s + 4s + 8 = 0
4
s
s
α3= 1/2
s
α4= 2/ε
s
s
4
3
2
1
0
3
2
1
2
8
2
4
0
0
8
0
ε >0
8
0
4-16/ε < 0
0
0
8
0
0
Hệ thống không ổn định, có 2 cực ở nửa phải mp phức
Tiêu chuẩn ổn định Routh
Các trường hợp đặc biệt
Trường hợp 2
Nếu tất cả các hệ số của hàng nào đó của bảng Routh bằng 0, ta thực
hiện như sau
• Thành lập đa thức phụ từ các hệ số của hàng trước hàng có tất cả
các hệ số bằng 0, gọi đa thức đó là A0(s)
• Thay hàng có tất cả các hệ số bằng 0 bởi một hàng khác có các hệ số
là hệ số của đa thức dA0(s)/ds, sau đó q trình tính tốn được tiếp
tục.
Tiêu chuẩn ổn định Routh
Ví dụ 5
Cho hệ thống có PTĐT sau
s5 + s 4 + 4s3 + 24s 2 + 3s + 63 = 0
s
s
α 3= 1
s
α4= -1/20
s
α5= -20/21
s
α5= 1/2
s
5
4
3
2
1
0
1
4
3
1
24
63
-20
-60
0
21
63
0
0
0
0
42
0
0
63
0
0
Hệ thống khơng ổn định, có 2 cực ở nửa phải mp phức