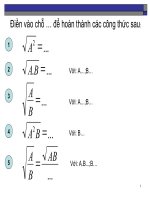<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1></div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>

Phương trình ax

2

+ bx + c = 0 (a ≠ 0)

• Nếu  > 0 phương trình có hai nghiệm phân biệt

x

₁

=

• Nếu  = 0 phương trình có nghiệm kép

x

₁

= x

₂

=

• Nếu  < 0 phương trình vơ nghiệm

2

b

b

; x

2a

2a



 









b

2a



</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>

2.Từ cơng thức nghiệm, hãy tính tổng và tích 2 nghiệm

của phương trình bậc hai một ẩn ax

2

_{+ bx + c = 0 (a  0)}

1 2

b

b

2b

b

x

x

2a

2a

2a

a



























2

1 2 ₂

2 2

2 2

b

b

b

x .x

.

2a

2a

4a

b

b

4ac

4ac

c

4a

4a

a





 





 















Nếu phương trình ax

2

+ bx + c = 0 (a  0) có nghiệm thì dù

đó là hai nghiệm phân biệt hay nghiệm kép ta đều có:

</div>
<span class='text_page_counter'>(4)</span><div class='page_container' data-page=4>

<b> Nếu x₁,x₂là hai nghiệm của phương </b>
<b>trình ax2 _{+ bx + c= 0 (a≠0) thì}</b>

1 2
1 2
b
x x
a
c
x .x
a







<b>?2 Cho ph ơng trình</b> <b>:2x2-5x +3 = 0(1)</b>
<b>a/Xác định a,b,c rồi tính a+b+c </b>

<b>b/ Chứng tỏ x₁=1 là một nghiệm của (1)</b>

<b>c/ Dùng định lí Vi-et để tính x₂</b>

<b> 2x2-5x +3 = 0(1)</b>

<b>a/a = 2;b =-5; c =3 ; a+b+c = 2-5+3 = 0 </b>
<b>b/ Thay x=1 vào (1)có: 2.1-5.1+3 = 0 </b>

<b>nên x =1 là một nghiệm của (1)</b>
<b>c/ Áp dụng định lí Vi-et ta có:</b>
<b>x₁. x₂= mà x</b>c_a 3₂ <b>₁=1 nên x₂=</b> 3₂

<b>Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có :</b>

• <b>a + b + c = 0 thì phương trình có nghiệm :</b>

<b>x₁ = 1 và x₂ =</b> c

a

<b>TỔNG QUÁT:</b>

</div>
<span class='text_page_counter'>(5)</span><div class='page_container' data-page=5>

<b> Nếu x₁,x₂là hai nghiệm của phương </b>
<b>trình ax2 _{+ bx + c= 0 (a≠0) thì}</b>

1 2

1 2
b
x x
a
c
x .x
a







<b>?3 Cho ph ơng trình</b> <b>:3x2+7x +4 = 0 (2)</b>
<b>a/Xác định a,b,c rồi tính a-b+c </b>

<b>b/ Chứng tỏ x₁=-1 là một nghiệm của (2)</b>

<b>c/ Dùng định lí Vi-et để tính x₂</b>
<b> 3x2-7x +4 = 0(2)</b>

<b>a/a = 3;b =7; c =4 ; a-+b+c = 3-7+4 = 0</b>
<b>b/ Thay x = -1 vào (2)có: </b>

<b> 3(-1)+7(-1)+4 = 0 </b>

<b>nên x =-1 là một nghiệm của (2)</b>

<b>c/ Áp dụng định lí Vi-et ta có:</b>

<b>x₁. x₂= mà x</b>_ac 4₃ <b>₁= -1 nên x₂=</b> ₃4

<b>Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có :</b>

• <b>a + b + c = 0 thì phương trình có nghiệm :</b>

<b>x₁ = 1 và x₂ =</b>

<b>a</b>
<b>c</b>

<b>TỔNG QUÁT:</b>

<b>GIẢI:</b>

• <b>a - b + c = 0 thì phương trình có nghiệm :</b>

<b>x₁ = -1 và x₂=</b>

<b>a</b>
<b>c</b>

</div>
<span class='text_page_counter'>(6)</span><div class='page_container' data-page=6>

<b> Giả sử hai số cần tìm có</b> <b>tổng bằng </b>
<b>S vµ tÝch b»ng P. Gäi mét sè lµ x thì </b>

<b>số kia là S - x. Theo giả thiết ta có ph </b>
<b>ơng trình </b>

<b>x(S </b><b> x) = P hay x2_{- Sx + P= 0.}</b>

<b>(1)</b>

<b>NÕu Δ= S2- 4P 0,</b>

<b>thì ph ơng trình (1) có nghiệm . Các </b>
<b>nghiệm này chính là hai số cần tìm</b>

<b> iu kiện để có hai số đó là S2 _-4P≥0</b>
<b>Nếu hai số cú tổng bằng S và tớch </b>

<b>bằng P thì hai số đó là hai nghiệm của </b>

<b>phương trình bậc hai x2_{- Sx + P = 0}</b>

<b>Ví dụ 1: Tìm hai số, biết tổng của </b>
<b>chúng bằng 27, tích của chúng bằng </b>
<b>180.</b>

<b>3</b>
<b>9</b> 



<b>Giải: Hai số phải tìm là nghiệm của </b>
<b>phương trình x2_{- 27x + 180 = 0}</b>

<b> = 272_{- 4.1.180 = 729-720 = 9;}</b>

<b>12</b>

<b>2</b>
<b>3</b>
<b>27</b>
<b>15</b>
<b>2</b>
<b>3</b>
<b>27</b>
<b>2</b>
<b>1</b> 





 <b>;</b> <b>x</b>

<b>x</b>

<b>Hai số cần tìm là 15 và 12</b>

<b>Ví dụ 2:Tính nhẩm nghiệm của phương </b>
<b>trình x2_{- 5x + 6 = 0}</b>

</div>
<span class='text_page_counter'>(7)</span><div class='page_container' data-page=7>

Đối với mỗi phương trình sau, kí hiệu x₁ và x₂ là hai nghiệm
(nếu có). Khơng giải phương trình, hãy điền vào những chỗ
trống (...).

a/ 2x2_{- 17x+1= 0, Δ =... x}

1+x2=... ; x1.x2=...

b/ 5x2_{- x- 35 = 0, Δ =... x}

1+x2=... x1.x2=...

c/ 8x2- x+1=0, Δ =... x

1+x2=... ; x1.x2=...

d/ 25x2_{+ 10x+1= 0, Δ =... x}

1+x2=... ; x1.x2=...

281 17

2

1
2

701 1

5 -7

-31

0 2

5

 1

25

</div>
<span class='text_page_counter'>(8)</span><div class='page_container' data-page=8>

Dùng hệ thức Vi-ét để tính nhẩm các nghiệm của

phương trình: a/ x

2

– 7x+12= 0 (1)

b/ x

2

+7x+13=0 (2)

a/

Δ =(7)2_{– 4.1.12 = 49 – 48 =1 > 0.}

Vì : 3 + 4 = 7 và 3. 4 = 12

nên x

₁

=3, x

₂

=

4

là hai nghiệm của phương trình (1)
b/ Δ =(-7)2_{– 4.1.13 = 49 – 52 = -3 < 0.}

</div>
<span class='text_page_counter'>(9)</span><div class='page_container' data-page=9>

<b>x</b>

<b>₁</b>

<b>= 1; x</b>

<b>₂</b>

<b>= -2</b>

<b>x</b>

<b>₁</b>

<b>= 1; x</b>

<b>₂</b>

<b>= -2</b>

<b>B</b>

<b>B</b>

<b>B</b>

<b>B</b>

<b>C</b>

<b>C</b>

<b>C</b>

<b>C</b>

<b>D</b>

<b>D</b>

<b>D</b>

<b>D</b>

<b> Phương trình vơ nghiệm</b>

<b>x</b>

<b>₁</b>

<b>= -1; x</b>

<b>₂</b>

<b>= -2</b>

<b>x</b>

<b>₁</b>

<b>= -1; x</b>

<b>₂</b>

<b>= -2</b>

<b>A</b>

<b>A</b>

<b>A</b>

<b>A</b>

<b>C</b>

<b>C</b>

<b>C</b>

<b>C</b>

<b>Nghiệm của phương trình 5x</b>

<b>2</b>

<b> – 15x+10 = 0 là:</b>

<b>Nghiệm của phương trình 5x</b>

<b>2</b>

<b> – 15x+10 = 0 l:</b>

<b>TRC NGHIM</b>

</div>
<span class='text_page_counter'>(10)</span><div class='page_container' data-page=10>

<b>Franỗois Viốte</b> (sinh 1540 - mất 13/02/1603)

tại Pháp.

-Ông là người đầu tiên dùng <b>chữ</b> để kí hiệu

<b>các ẩn, các hệ số</b> của phương trình và dùng

chúng để biến đổi và giải phương trình nhờ
cách đó mà nó thúc đẩy Đại số phát triển
mạnh.

</div>
<span class='text_page_counter'>(11)</span><div class='page_container' data-page=11>

<b>1.Cho phương trình 2x2_{- 3x + 1 = 0}</b>

<b>Gọi x₁, x₂ là các nghiệm của phương trình. Khơng giải phương trình; </b>
<b>hãy tính giá trị các biểu thức:</b>

<b>a/ ;</b> <b> b/ </b>
<b>c/ ;</b> <b>d/ </b>

<b>2.Gọi x₁ và x₂ là hai nghiệm của phương trình (k - 1) x2_{- 2kx + k - 4 = 0. Hãy}</b>

<b>tìm một hệ thức liên hệ giữa x₁ và x₂ không phụ thuộc tham số k</b>

1 2

1 1

x  x

1 2

1 2

1 x 1 x

x x

 



2 2

1 2

x x 1 2

2 1

x x

x 1 x 1

•<b> Làm bài tập 28; 29; 30; 33sgk</b>

•

<b> Chuẩn bị ‘‘Luyện tập’’</b>

<b>3.Tìm giá trị của m để phương trình x2_{– mx + m + 1 = 0 có nghiệm x}</b>
<b>1, x2</b>

</div>
<span class='text_page_counter'>(12)</span><div class='page_container' data-page=12>

<b>CHÚC</b>

<b> CÁC </b>

<b>EM</b>

<b> HỌC</b>

</div>

<!--links-->