MA TRẬN ĐỀ KIỂM TRA CHƯƠNG I, II: PHÉP BIẾN HÌNH – QUAN ...
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (107.73 KB, 3 trang )
<span class='text_page_counter'>(1)</span><div class='page_container' data-page=1>
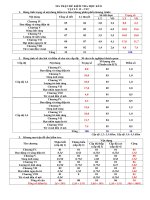
MA TRẬN ĐỀ KIỂM TRA
CHƯƠNG I, II: PHÉP BIẾN HÌNH – QUAN HỆ SONG SONG
Chủ đề/
Chuẩn KTKN
Cấp độ tư duy
Nhận biết Thông hiểu Vận dụng thấp Vận dụng cao Cộng
Phép tịnh tiến 2 3 1 6
Phép quay 2 1 1 4
Phép vị tự
Phép đồng dạng
1 1 2 1 5
Cộng 3
(20%)
6
(40%)
4
(27%)
2
(13%)
BẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎI ĐỀ KIỂM TRA
<i><b>I/ Trắc nghiệm: 6điểm</b></i>
CHỦ ĐỀ CÂU MÔ TẢ
Phép tịnh tiến 1 Nhận biết: Định nghĩa Phép tịnh tiến
2 Thơng hiểu: Tìm ảnh của 1 điểm qua phép tịnh tiến
3 Thơng hiểu: Tìm tạo ảnh của 1 điểm qua phép tịnh tiến
4 Thơng hiểu: Tìm phép tịnh tiến
5 Nhận biết: Tính chất của phép tịnh tiến
6 Vận dụng : Tìm ảnh của 1 đường thẳng qua phép tịnh tiến
Phép quay 7 Thơng hiểu: Tìm ảnh của 1 điểm qua phép quay tâm O một góc?
8 Vận dụng : Tìm ảnh của 1 đường trịn qua quay tâm O một góc ?
9 Thơng hiểu: Tính chất của phép quay
10 <sub>Vận dụng cao: Tìm ảnh của 1 đường thẳng qua quay tâm O một góc </sub> <sub>90</sub>0
<sub>?</sub>Phép vị tự -
phép đồng dạng
11 <sub>Nhận biết: Định nghĩa phép vị tự tâm O tỉ số </sub><i>k</i>
12 Vận dụng: Tìm ảnh của 1 điểm qua phép vị tự
13 Thông hiểu: Tìm ảnh của 1 đường trịn qua phép vị tự
<b>14</b> Vận dụng: Tìm ảnh của 1 đường thẳng qua phép vị tự
15 Vận dụng cao: Tìm ảnh của 1 điểm qua phép đồng dạng
Trắc nghiệm 15 câu mỗi câu 0.4 điểm (6đ)
<i><b>II/ Tự luận : 4 điểm </b></i>
</div>
<span class='text_page_counter'>(2)</span><div class='page_container' data-page=2>
<i><b>ĐỀ</b></i>
<i><b>Câu 1. Trong mặt phẳng tọa độ</b></i>
<i>Oxy</i>, cho phép biến hình
<i>F</i>
xác định như sau: Với mỗi điểm
;
<i>M x y</i>
ta có điểm
<i>M</i>
'
<i>F M</i>
sao cho
<i>M x y</i>
' '; '
thỏa mãn:
<i>x</i>' <i>x</i> 2; <i>y</i>' <i>y</i> 3. Mệnh đề nào sau
đây đúng:
<b>A. </b>
<i>F</i>
là phép tịnh tiến theo
<i>v </i>
2;3
.
<b>B. </b>
<i>F</i>
là phép tịnh tiến theo
<i>v </i>
2;3
.
<b>C. </b>
<i>F</i>
là phép tịnh tiến theo
<i>v </i>
2; 3
.
<b>D. </b>
<i>F</i>
là phép tịnh tiến theo
<i>v </i>
2; 3
.
<i><b>Câu 2. </b></i>
Trong mp Oxy cho điểm A(1; 2). Phép tịnh tiến theo<i>v</i>
1; 2
biến A thành điểm nào ?
<b>A. </b>A’(-2;0) <b>B. </b>A’(2;0) <b>C. </b>A’(0; -4) <b>D. </b>A’(0; 2)
<i><b>Câu 3. </b></i>
Trong mp Oxy điểm A’(2;- 5) là ảnh của điểm nào trong các điểm sau qua phép tịnh tiến theo
1; 3
<i>v</i>
<b>A. </b>A(1; 2) <b>B. </b>A(-3; 8) <b>C. </b>A(3; -8) <b>D. </b>A(1;-2)
<i><b>Câu 4. </b></i>
Trong mp Oxy, cho điểm A(3; -1) và B(1;2). Phép tịnh tiến theo<i>v</i>
biến A thành B thì:<b>A. </b>
<i>v </i>
3; 2
<b>B. </b>
<i>v </i>
2;3
<b>C. </b>
<i>v</i>
2; 3
<b>D. </b>
<i>v</i>
3; 2
<i><b>Câu 5. </b></i>
Trong mp Oxy cho d:2<i>x y</i> 3 0. Phép tịnh tiến theo vectơ<i>v</i>
1;2
biến d thành đt nào ?
<b>A. </b>2<i>x y</i> 2 0 <b>B. </b><i>x</i> 2<i>y</i> 1 0 <b>C. </b>2<i>x y</i> 1 0 <b>D. </b>2<i>x y</i> 1 0
<i><b>Câu 6. </b></i>
Phép tịnh tiến theo <i>v</i>
biến đường thẳng (d) thành (d’) khi đó
<b>A. </b>d’
d <b>B. </b>d’ // d <b>C. </b>d’ // d hoặc d’
d <b>D. </b>d’ cắt d<i><b>Câu 7. </b></i>
Trong mp Oxy cho điểm A(2; -3). Phép quay tâm O một góc
900<sub> biến A thành điểm?</sub><b>A. </b>A’(3; 2) <b>B. </b>A’(3; -2 <b>C. </b>A’(-3;2) <b>D. </b>A’(-3;-2)
<i><b>Câu 8. </b></i>
Phép quay tâm O một góc
900<sub> biến đường thẳng (d) thành (d’) khi đó:</sub><b>A. </b>d’ // d <b>B. </b>d’ d <b>C. </b>Đáp án khác <b>D. </b>d’
d<i><b>Câu 9. </b></i>
Trong mp Oxy cho d:<i>x y</i> 3 0. Phép quay tâm O một góc
900<sub> biến d thành đt nào ?</sub><b>A. </b><i>x y</i> 3 0 <b>B. </b><i>x y</i> 3 0 <b>C. </b><i>x y</i> 3 0 <b>D. </b><i>x y</i> 3 0
<i><b>Câu 10. </b></i>
Cho phép biến hình f biến điểm d thành d’ sao cho d’ d. Vậy f là phép biến hình nào sao đây:<b>A. </b>Phép quay <b>B. </b>Phép vị tự <b>C. </b>Phép tịnh tiến <b>D. </b>Đáp án khác
<i><b>Câu 11. </b></i>
Cho phép biến hình f biến điểm M thành M’ sao cho<i>OM</i>
' 2
<i>OM</i>
(O là điểm cố định cho trước).
Vậy f là phép biến hình nào sao đây:
<b>A. </b>Phép vị tự <b>B. </b>Phép quay <b>C. </b>Phép đối xứng tâm O <b>D. </b>Phép tịnh tiến
<i><b>Câu 12. </b></i>
Trong mp Oxy cho điểm A(2; -4). Phép vị tự tâm O tỉ số1
2
<i>k </i>
biến A thành điểm nào trong các
điểm sau ?
<b>A. </b>A’(1;-2) <b>B. </b>
<i>A</i>
' 4; 8
<b>C. </b><i>A</i>
' 4;8
<b>D. </b><i>A</i>
' 1;2
<i><b>Câu 13. </b></i>
Trong mp Oxy cho (C):
2 2
1 2 4
<i>x</i> <i>y</i>
. Phép vị tự tâm O tỉ số
<i>k </i>
2
biến (C) thành đ.trònnào ?
<b>A. </b>
2 2
2
4
4
<i>x</i>
<i>y</i>
<sub> </sub><b><sub>B. </sub></b>
<i>x</i>1
2
<i>y</i> 2
216<b>C. </b>
2 2
2 4 16
<i>x</i> <i>y</i>
<b>D. </b>
2 2
1 2 4
</div>
<span class='text_page_counter'>(3)</span><div class='page_container' data-page=3>
<i><b>Câu 14. </b></i>
Trong phép vị tự tâm O tỉ số k = 2, nếu điểm M chạy trên đường thẳng d: <i>x</i>3<i>y</i> 4 0 thì ảnh M’của M chạy trên đường thẳng nào sau đây:
<b>A. </b><i>x</i> 3<i>y</i> 8 0 <b>B. </b><i>x</i>3<i>y</i> 8 0 <b>C. </b><i>x</i>3<i>y</i> 8 0 <b>D. </b><i>x</i> 3<i>y</i> 8 0
<i><b>Câu 15. </b></i>
Trong mp Oxy, cho điểm M(1; -4). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếpphép tịnh tiến theo vectơ
<i>v</i>
1; 2
và phép vị tự tâm O tỉ số k = 2 sẽ biến M thành điểm nào trong các điểm sau?
<b>A. </b>C(0; 12) <b>B. </b>D(0; -12) <b>C. </b>B(2; -2) <b>D. </b>A(4;
<i><b>-4)---TỰ LUẬN: 4Điểm</b></i>
<i><b>Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M và N lần lượt là trung điểm của SA, SB,</b></i>
<i>1) Chứng minh: MN // CD .</i>
<i>2) P nằm trên cạnh SD. Tìm giao tuyến của (MNP) và (SCD)</i>
<i><b>Bài 2: Cho tứ diện ABCD . Gọi I, J là trung điểm của BC và CD</b></i>
1) Chứng minh rằng BD//(AIJ).
2) Gọi K là điểm trên cạnh AB. Tìm thiết diện của tứ diện và mp(IJK).
</div>
<!--links-->