T/c hai tiếp tuyến cắt nhau
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (389.2 KB, 11 trang )
KÍNH CHÀO QUÝ THẦY CÔ GIÁM
KHẢO VÀ CÁC EM HỌC SINH
,
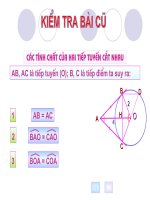
KIỂM TRA BÀI CŨ
Cho AB và AC là hai tiếp tuyến tại B và C
của đường tròn (O) . Chứng minh : AB = AC ,
góc OAB = góc OAC , góc AOB = góc AOC
ĐỊNH LÍ
•
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại
một điểm thì :
•
Điểm đó cách đều hai tiếp điểm
•
Tia kẻ từ điểm đó đi qua tâm là tia phân giác
của góc tạo bởi hai tiếp tuyến
Tia kẻ từ tâm đi qua điểm đó là tia phân giác của
góc tạo bởi hai bán kính đi qua các tiếp điểm
1. Đònh lí về hai tiếp tuyến cắt nhau
§6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU
A
B
C
O
A
B C
D
E
F
Vì I thuộc tia phân giác góc B nên ID = IF (1)
Vì I thuộc tia phân giác góc C nên ID = IE (2)
Từ (1) và (2) suy ra : ID = IE = IF
Hay ba điểm D, E , F nằm trên cùng một đường tròn ( I )
I
§6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU
2. Đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của một tam giác
gọi là đường tròn nội tiếp tam giác , còn tam giác
gọi là ngoại tiếp đường tròn
D
E
F
A
B
C
BÁN KÍNH
TÂM
I
§6. TÍNH CHẤT CỦA HAI TIẾP TUYẾN CẮT NHAU