D01 tìm tâm và bán kính, đk xác định mặt cầu muc do 4
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (230.99 KB, 3 trang )
Câu 42: [2H3-2.1-4](THPT CHUYÊN KHTN - LẦN 1 - 2018) Trong không gian với hệ tọa độ Oxyz ,
cho hai điểm A 5;0;0 và B 3; 4;0 . Với C là điểm nằm trên trục Oz , gọi H là trực tâm của
tam giác ABC . Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán
kính của đường tròn đó bằng
A.
5
.
4
B.
3
.
2
C.
5
.
2
D.
3.
Lời giải
Chọn A
z
C
H
y
O
K
B
E
Ax
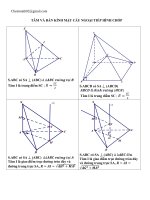
Ta có C 0;0; c . Dễ thấy tam giác ABC cân tại C . Gọi E 4; 2;0 là trung điểm của AB .
AB OC
Ta có mặt phẳng OCE vuông góc với AB (do
) và là mặt phẳng cố định.
AB CE
Gọi K là trực tâm tam giác OAB , do A , B và K cùng nằm trong mặt phẳng Oxy nên
x 3
OK . AB 0
x. 2 y.4 0
3
3 . Tìm được K 3; ;0 .
2
BK .OA 0
x 3 0
y 2
AB OEC HK AB
Ta chứng minh được KH CAB do
.
HK
CA
CA
BHK
Suy ra
KHE 90 . Suy ra
H
thuộc mặt cầu đường kính
KE 1
1
5
và
4
2
3
d B, SCD d H , SCD thuộc mặt phẳng OCE cố định. Vậy H luôn thuộc một
2
5
.
4
Câu 35. [2H3-2.1-4] (Đề thi lần 6- Đoàn Trí Dũng - 2017 - 2018)Trong không gian với hệ trục tọa độ
Oxyz , viết phương trình mặt phẳng P đi qua điểm M 1;1; 2 , đồng thởi cắt 3 trục tọa độ lần
đường tròn cố định có bán kính R
lượt tại các điểm A, B, C sao cho M là trực tâm tam giác ABC .
x y z
A. x y 2 z 6 0 . B. 3 0 . C. x y 2 z 4 0 .
1 1 2
Lời giải
D. x y 2 z 2 0 .
Chọn A
Gọi H là chân đường cao kẻ từ A của tam giác ABC .
OA OB
Ta có:
OA OBC OA BC .
OA OC
Mặt khác: BC AH nên BC OAH BC OM .
Tương tự ta có: AB OM .
Vậy OM ABC . Suy ra nP OM 1;1; 2 .
Phương trình mặt phẳng P : x y 2 z 6 0 .
Câu 39: [2H3-2.1-4] [MINH HỌA L2] [2017] Trong không gian với hệ tọa độ Oxyz, xét các điểm
A 0;0;1 , B m;0;0 , C 0; n;0 , D 1;1;1 với m 0; n 0 và m n 1. Biết rằng khi m ,
n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng ABC và đi qua d . Tính bán
kính R của mặt cầu đó?
B. R
A. R 1 .
2
.
2
C. R
3
.
2
D. R
3
.
2
Lời giải
Chọn A
Gọi I 1;1;0 là hình chiếu vuông góc của D lên mặt phẳng (Oxy)
Ta có: Phương trình theo đoạn chắn của mặt phẳng ( ABC ) là:
x y
z 1
m n
Suy ra phương trình tổng quát của ( ABC ) là nx my mnz mn 0
Mặt khác d I ; ABC
1 mn
m n m n
2
2
2
2
1 (vì m n 1) và ID 1 d ( I ; ABC .
Nên tồn tại mặt cầu tâm I (là hình chiếu vuông góc của D lên mặt phẳng Oxy ) tiếp xúc với
( ABC ) và đi qua D . Khi đó R 1 .
Câu 383: [2H3-2.1-4] [CHUYÊN ĐHKHTN HUẾ - 2017] Trong không gian với hệ tọa độ Oxyz , cho
điểm A 0;0; 4 , điểm M nằm trên mặt phẳng Oxy và M O . Gọi D là hình chiếu vuông
góc của O lên AM và E là trung điểm của OM . Biết đường thẳng DE luôn tiếp xúc với một
mặt cầu cố định. Tính bán kính mặt cầu đó.
A. R 2 .
D. R 2 .
C. R 4 .
B. R 1 .
Lời giải
Chọn A
A
I
D
O
M
E
Ta có tam giác OAM luôn vuông tại O .
Gọi I là trung điểm của OA (Điểm I cố định)
Ta có tam giác ADO vuông tại D có ID là
1
đường trung tuyến nên ID OA 2 1
2
Ta có IE là đường trung bình của tam giác OAM
nên IE song song với AM mà OD AM OD IE
Mặt khác tam giác EOD cân tại E . Từ đó suy ra
IE là đường trung trực của OD
Nên DOE ODE; IOD IDO IDE IOE 90 ID DE 2
Vậy DE luôn tiếp xúc với mặt cầu tâm I bán kính R
OA
2.
2