D01 tìm tâm và bán kính, đk xác định mặt cầu muc do 3
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (210.48 KB, 3 trang )
Câu 38.
[2H3-2.1-3] (THPT Lục Ngạn-Bắc Giang-2018) Trong không gian với hệ tọa
độ Oxyz , cho A 2;0;0 , B 0; 2;0 , C 0;0; 2 . Bán kính mặt cầu nội tiếp tứ diện OABC bằng
2
.
3 3
5
.
62 3
A.
B.
4
.
3 2 3
C.
3
.
62 3
D.
Lời giải
Chọn A
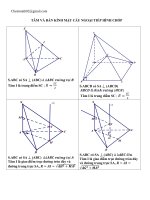
Dễ thấy O. ABC là hình chóp đều, ABC đều cạnh 2 2 .
Do đó diện tích toàn phần của tứ diện OABC là: Stp 3SOAB SABC 6 2 3 .
1
4
Mà VOABC .OA.OB.OC .
6
3
Ta có bán kính mặt cầu nội tiếp tứ diện OABC là r
3VOABC
4
2
.
Stp
6 2 3 3 3
Câu 33. [2H3-2.1-3] (THPT Chuyên Vĩnh Phúc- Lần 3-2018) Trong không gian với hệ trục
tọa độ Oxyz , cho hai điểm A 1;0; 3 , B 3; 2; 5 . Biết rằng tập hợp các điểm M trong
không gian thỏa mãn đẳng thức AM 2 BM 2 30 là một mặt cầu S . Tọa độ tâm I và bán
kính R của mặt cầu S là
A. I 2; 2; 8 ; R 3 .
B. I 1; 1; 4 ; R 6 .
C. I 1; 1; 4 ; R 3 .
D. I 1; 1; 4 ; R
30
.
2
Lời giải
Chọn C
Gọi tọa độ điểm M x; y; z . Khi đó AM 2 BM 2 30
x 1 y 2 z 3 x 3 y 2 z 5 30
2
2
2
2
2
2 x2 2 y 2 2 z 2 4 x 4 y 16 z 18 0
x2 y 2 z 2 2 x 2 y 8z 9 0
x 1 y 1 z 4 9 là phương trình của mặt cầu S , có tâm I 1; 1; 4 và
2
2
2
bán kính R 3 .
Câu 10:
[2H3-2.1-3] (THPT Chuyên ĐHSP Hà Nội - Lần I - 2017 - 2018) Trong không gian
với hệ tọa độ Oxyz , cho các điểm A 0;0; 2 , B 4;0;0 . Mặt cầu S có bán kính
nhỏ nhất, đi qua O , A , B có tâm là
A. I 0;0; 1 .
2
4
I ;0; .
3
3
B. I 2;0;0 .
C. I 2;0; 1 .
D.
Lời giải
Chọn C
Gọi J là trung điểm AB J 2;0; 1
Tam giác ABO vuông tại O nên J là tâm đường tròn ngoại tiếp tam giác OAB .
Gọi I là tâm mặt cầu S , S qua các điểm A, B, O .
Ta có đường thẳng IJ qua J và có một VTCP là j 0;1;0 nên có PTTS
x 2
y b .
z 1
I IJ I 2; b; 1 ,IA b2 5 IA 5 .
Dấu bằng xảy ra khi b 0
Vậy I 2;0; 1 .
Câu 24: [2H3-2.1-3] (THTT - Số 484 - Tháng 10 - 2017 - BTN) Trong không gian với hệ trục
tọa độ Oxyz , cho ba điểm A 1; 2; 4 , B 1; 3;1 , C 2; 2;3 . Tính đường kính l của
mặt cầu S đi qua ba điểm trên và có tâm nằm trên mặt phẳng Oxy .
B. l 2 41 .
Lời giải
A. l 2 13 .
C. l 2 26 .
D. l 2 11 .
Chọn C.
Gọi tâm mặt cầu là : I x; y; 0 .
IA IB
IA IC
x 1 y 2
2
42
x 1 y 3
x 1 y 2
2
42
x 2 y 2
2
2
2
2
2
2
y 2 4 y 3 1
2
2
x 2 x 1 16 x 4 x 4 9
10 y 10
x 2
l 2R 2
2 x 4
y 1
2
2
3 1
2
2
2
2
12
32
42 2 26 .
Câu 8085:
[2H3-2.1-3] [TT Hiếu Học Minh Châu-2017] Trong không gian với hệ trục tọa
độ Oxyz , cho mặt cầu S đi qua điểm A 2; 2;5 và tiếp xúc với các mặt phẳng
: x 1 , : y 1 , : z 1 . Bán kính mặt cầu S bằng.
A. 3 .
B.
33 .
C. 3 2 .
Lời giải
Chọn A
Gọi I a; b; c là tâm mặt cầu.
D. 1 .
a 1 b 1 (*)
Ta có: a 1 c 1 (**)
.
2
2
2
2
a 1 a 2 b 2 c 5 (***)
b c
Từ (*) (**)
.
b c 2 0
Xét b c :
a c
- Từ (**)
.
a c 2
a 4
- Với a c thay vào (***) b 4 R a 1 3 .
c 4
Tương tự các trường hợp khác. Chọn A.
Câu 8090:
[2H3-2.1-3] [Sở GD và ĐT Long An-2017] Trong không gian với hệ tọa độ
x 1 y z 1
. Gọi P là mặt
Oxyz , cho điểm I 2; 1; 6 và đường thẳng :
1
2
2
phẳng thay đổi luôn chứa đường thẳng ; S là mặt cầu có tâm I và tiếp xúc mặt
phẳng P sao cho mặt cầu S có bán kính lớn nhất. Tính bán kính R của mặt cầu
S .
A. R 5 .
B. R 3 2 .
C. R 2 5 .
D. R 2 3 .
Lời giải
Chọn B
Gọi H là hình chiếu của I lên .
Ta có: IH d I , d I , P .
Gọi là mặt phẳng chứa I và vuông góc .
Ta tìm được : x 2 y 2 z 12 0 .
Tọa độ H là giao điểm của và nên là nghiệm của hệ phương trình:
x 1 t
t 1
y 2t
x 2
.
z 1 2t
y 2
x 2 y 2 z 12 0 z 3
Vậy: H 2; 2; 3 .
Bán kính R IH 02 32 32 3 2 .