D11 thiết diện vuông góc với đường thẳng muc do 4
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (247.14 KB, 4 trang )
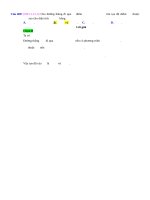
Câu 43: [1H3-3.11-4] (THPT Hậu Lộc 2 - Thanh Hóa - 2017 - 2018 - BTN) Cho hình chóp
S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SB
tạo với đáy góc 450 . Một mặt phẳng đi qua A và vuông góc với SC cắt hình chóp
S. ABCD theo thiết diện là tứ giác ABCD có diện tích bằng:
A.
a2 3
.
4
B.
a2 3
.
2
C.
a2 3
.
6
D.
a2 3
.
3
Lời giải
Chọn C
S
C'
D'
I
B'
A
D
O
B
C
Dễ thấy SBA 45 . Ta có BD SC và BD SC và SC không vuông góc với mặt phẳng
SBD , suy ra BD / / BD . Nên từ I SO AC nên từ I kẻ BD / / BD cắt SB , SD lần lượt
tại B , D .
AB SC
Từ trên suy ra BD AC và
AB SB .
AB BC
Suy ra S ABCD
Vậy S ABC D
Câu 1791.
1
a 6
a 2
BD SB a 2
1
và
.
AC .BD . Mà AC
BD
3
2
2
BD
SB 2.a 2 2
1
3 2
AC .BD
a .
2
6
[1H3-3.11-4] Cho tứ diện SABC có hai mặt ABC và SBC là hai tam giác đều cạnh
3
. M là điểm trên AB sao cho AM b 0 b a . P là mặt phẳng qua M và
2
vuông góc với BC. Thiết diện của P và tứ diện SABC có diện tích bằng?
a , SA
a
3 3 a b
A.
.
.
4 a
2
3 a b
B.
.
.
4 a
2
3 3 a b
C.
.
16 a
2
Lời giải
Chọn C
3 3 a b
D.
.
8 a
2
Gọi N là trung điểm của BC .
SB
AB
SC
AC
BC
BC
Theo bài ra BC
SN
AN
P
Kẻ MI / / AN , MK / / SA
SABC là
BC
M
SAN .
P
P / / SAN
Thiết diện của P và tứ diện
KMI .
ABC
là hai tam giác đều cạnh a
SBC
a 3
2
.
AN
a 3
2
SM
SA
SAN là tam giác đều cạnh
2
3 a b
KMI là tam giác đều cạnh
.
2
a
S
KMI
3 3 a b
.
.
16
a
Câu 15: [1H3-3.11-4] (Chuyên Phan Bội Châu - Nghệ An - Lần 1 - 2017 - 2018 - BTN) Cho hình
chóp đều S. ABCD có tất cả các cạnh bằng a , điểm M thuộc cạnh SC sao cho SM 2MC .
Mặt phẳng P chứa AM và song song với BD . Tính diện tích thiết diện của hình chóp
S. ABCD cắt bởi P .
A.
3a 2
.
5
B.
4 26a 2
.
15
C.
Lời giải
Chọn C
2 26a 2
.
15
D.
2 3a 2
.
5
S
N
A
B
I
M
O
P
C
D
Gọi O AC BD , I AM SO .
Trong SBD từ I kẻ đường thẳng song song với BD cắt SB , SD lần lượt tại N , P .
Suy ra thiết diện là tứ giác ANMP .
BD AC
BD SAC
Ta có:
BD SO
BD AM .
Mặt khác: BD / / NP .
AM NP .
S ANMP
1
NP. AM .
2
+ Tính AM :
SA SC a
Ta có:
SAC vuông cân tại S .
AC a 2
2
a 13
2
AM SA SM a a
.
3
3
2
2
2
+ Tính AM :
Ta có: NP / / BD
Tính
SI
:
SO
NP SI
SI .BD
.
NP
BD SO
SO
S
M
I
A
Gọi
O
SI
k.
SO
Ta có: AI AS SI SA kSO .
2
AM AS SM SA SC .
3
2
A , I , M thẳng hàng AI l AM SA k SO lSA lSC
3
4
1
k
k l 1
k
2
2
5
.
SA SA SC lSA lSC
2
3
l 3
1 k 2 l 0
2
5
3
SI 4
4
4a 2
.
NP BD
SO 5
5
5
S ANMP
1
1 4a 2 a 13 2 26a 2
.
.
NP. AM .
2 5
15
3
2
C