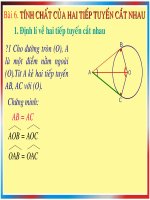Tính chất hai tiếp tuyến cắt nhau
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (857.64 KB, 15 trang )
GD
KI M TRA BAØI CỂ Ũ
•
HS1: Nhắc lại định lí về tiếp tuyến của
đường tròn?
•
HS2: Làm bài tập sau:
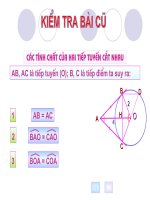
a/ Qua điểm A nằm ngoài đường tròn (O)
hãy kẻ các tiếp tuyến AB, AC tại B và C
của đường tròn (O)?
b/ Có nhận xét gì về hai tam giác OAB và
OAC?
•
Xác định tâm của một hình tròn:
V
ô
ù
i
“
t
h
ö
ô
ùc
p
h
a
ân
g
i
a
ù
c
”
,
t
a
c
o
ù
t
h
e
å
t
ì
m
ñ
ö
ô
ï
c
t
a
â
m
c
u
ûa
m
o
ä
t
v
a
ä
t
h
ì
n
h
t
r
o
ø
n
?
Bµi 6. TÝnh chÊt cña hai tiÕp tuyÕn c¾t nhau
.O
B
C
A
Cho h×nh 79 trong ®ã AB, AC theo
thø tù lµ c¸c tiÕp tun t¹i B, t¹i C
cđa ®êng trßn (O). H·y kĨ tªn mét
vµi ®o¹n thẳng b»ng nhau, mét vµi
gãc b»ng nhau trong h×nh.
?1
H×nh 79
)
)
Khi AB, AC lµ c¸c tiÕp tun t¹i B,
t¹i C cđa ®êng trßn (O):
. AB = AC
. BAO = CAO
. BOA = COA
?1
- Góc BAC là góc tạo bởi hai tiếp tuyến
- Góc BOC là góc tạo bởi hai bán kính
* §Þnh lÝ:
NÕu hai tiÕp tun cđa mét ®êng trßn c¾t nhau t¹i mét
®iĨm th×:
. §iĨm ®ã c¸ch ®Ịu hai tiÕp ®iĨm.
. Tia kỴ tõ ®iĨm ®ã qua t©m lµ tia ph©n gi¸c cđa gãc t¹o bëi
hai tiÕp tun.
. Tia kỴ tõ t©m ®i qua ®iĨm ®ã lµ tia ph©n gi¸c cđa gãc t¹o
bëi hai b¸n kÝnh ®i qua c¸c tiÕp ®iĨm.
Bµi 6. TÝnh chÊt cđa hai tiÕp tun c¾t nhau
XÐt ∆OAB vu«ng t¹i B vµ ∆OAC vu«ng t¹i C cã:
OA lµ c¹nh chung
OB = OC (b¸n kÝnh (O))
Do đoù:∆OAB = ∆OAC (c¹nh huyÒn- c¹nh gãc vu«ng)
*§Þnh lÝ (SGK/114)
B, C
∈
(O)
AB, AC lµ hai tiÕp tuyÕn cña (O)
Ta cã: AB, AC lµ hai tiÕp tuyÕn cña (O) t¹i B vµ C (gt)⇒ AB ⊥ OB, AC ⊥
OC.
Chøng minh
+ AB = AC
+ Tia AO lµ ph©n gi¸c BAC
+ Tia OA lµ ph©n gi¸c BOC
⇒
⇒
AB = AC
AB = AC
BAO = CAO nªn AO lµ tia ph©n gi¸c cña BAC
BOA = COA nªn OA lµ tia ph©n gi¸c cña BOC.
GT
KL
.O
B
C
A
)
)
Bµi 6. TÝnh chÊt cña hai tiÕp tuyÕn c¾t nhau