GS. TS. PHẠM NGỌC KHÁNH (Chủ biên)
Th.s. VŨ VĂN THÀNH

BÀI TẬP
SỨC BỂN VẬT LIỆU
■

(Tái bản)

NHÀ XUẤT BẢN XÂY DựNG
HÀ N Ộ I-2010

■


LỜI NÓI ĐẦU

&'ểc bền vật liệu là m ôn cơ sở kỹ th u ậ t quan trọng của n hiều n g à n h chuyên môn,
đậc úột là các ngà n h xây dựng công trình ưà c h ế tạo cơ khí, được g iả n g dạy trong
nhừ.i trường đ ai hoc kỹ thuật. Nó củng là m ột m ôn học có tín h thực hàn h, đòi hỏi
ngưd học p h ả i biết vận đ ụ n q lý thuyết dê g iải n h ữ n g bài toán đa d ạ n g của thực tế
hoặ gầ n g ũ i với thực tế.
làm công tác g iả n g d ạ y nhiều năm , chúng tôi th ấy sin h viên còn rấ t n h iều lú n g
túỉiị trong việc g iả i bài tập m ôn sức bền vật liệu, trong k h i các sách th a m khảo lại
quáít, đặc biệt là các sách bài tập. Đây là m ột khó k h ă n rất lớn đôi với sin h viên,
đặc'liệt hiện na y hệ đào tạo tại chức, hệ đào tạo từ xa của các trường kỹ th u ậ t đã
m ở ' h ầ u hết trên các vùng, m iền của đ â t nước. Đỗi với các hệ đào tạo n à y lại càng
khó th ă n hơn .
ỉ ỉ g iá m bớt m ộ t p h ầ n khó kh ă n trên, chứng tôi biên soạn cuốn sách "B à i tậ p
S ứ íb è n v â t liêu".
N )1 d u n g cuốn sách trước hết là những bài tập về các kiến thức cơ bần của môn

học nà ch úng tôi đã trin h bày các bước giải cụ th ế n h ằ m giúp các bạn sin h viên nắm
đượ các kiến thức cơ bản môn học, các phương p há p g iả i bài tập đê nâ ng cao kỹ năng
th ự ih à n h , sau đỏ còn có các bài tập chọn lọc khác và các đ ề thi, đáp án thi O lym pic
cư h c toàn quốc m ôn Sứ c bền vật liệu từ năm 1989 đến n ă m 2005 - đây là các bài tộ.p
ở irìc độ cao hớn đ ế giú p các sinh viên giỏi rèn luyện thêm năng lực của m inh.
(uôh sách gồm 3 p h ẩ n : Phần A - Tóm tắt lý thuyết, P hầ n B - H ướng d ẫ n giả i và
bài ập chọn lọc, P h ẩ n c - Đề thi O lym pic cơ học toàn quốc m ôn S B V L và đáp án từ
năn 1989 đến 2005.
l y vọng rằng cuôh sách này sẽ g iú p ích cho sin h viên trong quá trìn h học tập
môì học, nó có thê là m ột "người thày" luôn luôn bên cạnh các bạn. N ó củ ng có thê
làirdài liệu th a m khảo cho nhữ ng người muôn đi sâu nghiên cứu m ôn học này.
lo trìn h độ và thời g ia n hạn c h ế nên cuốn sách này chắc chắn vòn n hiều khiếm
kh ư ết, ch ủ n g tôi, m ong nhận được nhiều ý kiến đóng góp q u ý báu của bạn đọc đ ể
sứa^hữa và hoàn thiện cho lần x u â t bản sau. Mọi ý kiến đóng góp xin g ử i về: N hà
xuâ bàn X à V dựng, 37 Lẻ Đ ại H ành, H à Nội.

C á c t á c g iả

3


PHẨN A

TÓM TẮT LÝ THUYẾT

Chương 1
KÉO NÉN ĐÚNG TÂM
+ Nội iực trên mặt eắí ngang: Chỉ có lực dọc Nz. Nz > 0 khi là lực kéo, N z < 0 khi là
lực nén.
* Xác định nội lực bằng phương pháp mặt cắt.

+ ứng suất trên mặt cắt ngang:

ơ z > 0 khi là ứng suất kéo, ơ z < 0 khi là ứng suất nén.
+ Ưng suất trẽn mật nghiêng u:
ơ u = ơ z cos (X

trong đó: a là góc hợp bởi phương của các pháp tuyến của mặt cắt nghiêng u và mặt cắt
ngang z. I > 0 khi nó làm cho phần xét quay thuận chiều kim đồng hồ.
* Biến dạng:
+ Biến dạng dọc:
trong đó n là số đoạn của thanh.
Nếu đoạn nào có N z, EF = const thì:

EF
+ Điều kiện bền cứa thanh:

ơ m.ix - H
ơ mm ^ M n

+ Điều kiện cứng của thanh: ầC < [Aí]
+ Theo dạng hình học:
Có 2 loại bài tập: Loại một thanh và loại hệ thanh.
5


+ Theo dạng kết cấu:
Có 2 loại: Loại kết cấu tĩnh định và loại kết cấu siêu tĩnh. Với loại bài toán siêu tĩnh,
ngoài các phương trình cân bằng tĩnh học ta còn phải thêm các phương trình bổ sung, đó
là các điều kiện biến dạng của hệ.


Chương 2
TRANG THÁI ÚNG SUÂT
+ Trạng thái ứng suất (TTUS) tại một điểm: Là tập hợp tất cả các ứng suất trên các mặt của
phân tô'hình hộp bao quanh điểm đó, bao gồm: ơ x, ơ , a z, T , T x, ĩ
Tuy nhiên do luật đối ứng của ứng suất tiếp đã có: T

, T , Tzx , Txz .

= Tyx, Tyz = T , Txz = Tzx.

+ Các loại TTUS. Gồm có 3 loại: TTUS khối, TTUS phảng, TTUS đơn. Chú V rang
trong trong tất cả các TTUS thì các ứng suất chính (USC) đều là các ứng suất cực trị.
+ Nghiên cứu TTUS: Mục đích nhàm xác định các ứng suất pháp cực trị (các USC),
ứng suất tiếp cực trị và phương của chúng.
+ TTUS phẳng:
Phân tố ở TTUS phẳng bao gồm các ứng suất (nếu đầy đủ): ơ x, ơ y,Txy = Ty x .
Úng suất trên mặt nghiêng u:
ơ

u

ƠX4 Ơ V ỡ - 0
— ^— 1^ + — ------ —c o s 2 a - Txv sin 2 a

2

2

~ ơ y


Xuv

2

sin 2 a + Txy c o s 2 a

Úng suất chính:

Phương của USC:

tg a m u x

Tx ỵ

ơ

Txy
ơ y

ơ x

^m in

Luât bất biến của TTUS có: ơ v + ơ v = ơ m, t + ơ mi„ = const
A

Úng suất tiếp cực trị:

Y


m ax

rnm

Tmux = ±
min

Phương của UST cực trị: Pmax = a mux + 45°
Cũng có thế xác định tất cả các đại lượng trên bằng vòng tròn Mo ứng
vòng Mo. Có thể vẽ vòng Mo bằng cách dựng hình hoặc xác định
cực p nằm trên vòng tròn (xem hình 1):
6

suất. Cách vẽ

tâm c vàmột

điếm


H ình 1
l ầ m c có toạ độ c

/ ơ_ . +, ơ_ v
-

'

\


> ,0

, cực p có toạ độ p ( ơ y, Txy)

V

ứng suất tiếp, các u s c ơ n

= - ơ min = M

v à

a max =

450

n ế u

T < 0

và cxmax -

- 4 5 °

nếu

X> 0 .
+ TTƯS khối:
Định luật Hooke:


8, = —[ơ ị

+ ơ 3)]

_Ị_
e2 = g [ ơ 2 - ^ ( ơ ^ + ơ , ) ]
E
_Ị_
= - ^ [ ơ , - ^ ( ơ , + ơ 2)]
b
E
hoặc:

1
8 X

x

=

x - ^ ( ơ y + ơ z)

E

ỵ
8y = p [ ơ y ~ ^ K + ơ *)]
E
1
e7 = — y? - n ( ơ x + ơ y)
E

va:

*y
Yxy =

Yyz = ■

G
T ,v

trong đó:

G=

2(l+n)
7


Chương 3
CÁC THUYẾT BỂN
+ Thuyết bền (TB) ứng suất pháp lớn nhất (TB1):
<*max ^

H

k

ơ » n in ^ H N
+ Thuyết bền biến dạng dài tương đối lớn nhất (TB2):
a gh

ơ„ = ơ , - f i ( ơ 2 + ơ , ) < ^ = [ơ]K

:

ơ„ = ơ 3 - ^ ( ơ , + ơ 2) < ^ = [ ơ ] n

+ Thuyết bền ứng suất tiếp lớn nhất (TB3):
ơ„ = ơ, - ơ 3 < [ơ ]
+ Thuyết bền thế năng biến đổi hình dáng (TB4):

Ơ<’ = ] Ị Ị ( ơ * - ơ y ) M ơ y " ơ /J? + ( ơ /.-"ơ *)2 + 3 ( Tỉ y +1i

+ Thuyết bển Mo:

ơ„ = ƠJ -

+ T» )

j^ -ơ 3 < [ ơ |
M

n

Chương 4
ĐẶC TRƯNG HÌNH HỌC CỦA HÌNH PHANG
+ Mômen tĩnh:

s x = jyd F ;

Sy = JxdF


F

F

Gọi C(xc , yc ) là trọng tâm mặt cắt thì:

Y c=^
c
F
xc

8

F

(m')

< [crj


và nỉu hình phảng F được chia thành n hình đơn giản thì:
Ẻ y ClF,

Ỉ * G F|
;
Ẻ F ,i
i=i

y c = - v ẳF,

ỉ—I

-+ Mômen quán tính (MMQT):
MMQT trục:

K - f y 2dF
F
Jy =

j x 2dF
F

MMQT ly tâm:

■^xy == jxydF
F

MMQT cực:

J p = J p 2dF
F

hoặc:

(m 4)
(m 4)
(m 4)

J p = | ( x 2 + y 2)dF = J x + J


4 Hệ trục quán tính chính trung tâm và M M QT chính trung tâm:
Hệ trục xy là hệ trục quán tính chính trung tâm nếu có: J xy = 0 và gốc toạ độ tại
trọng tâm c của mặt cắt.
Chú v: Nếu hệ trục xy có một trục là trục đối xứng của mạt cắt và có gốc toạ độ tại
trọng tâm c của mặt cắt thì nó là hẹ trục quán tính chính trung tâm của mật cắt đó.
MMQT của hình F đối với hệ trục quán tính chính trung tâm được gọi là M M Q T
chírh trung tâm của hình F.
MMQT của một sô hình thường gặp:
• Hình chữ nhật:
J _ bh3 ;
12
V

-

J y -_ hb3
12

'Hình vành giếng:
J D
J v

=

2

7ĩ R

j


4

b

JP * 0 .1 D 4(1 - V )
J ~ 0 , 1D4 (1 - I ] 4) với r| =

Ilình 2

Hình 3

D

' ới hình tròn thì ỉ] = 0

9


yn

Hình tam giác:
_ bh3
X -

—

_ bh3
;

Xo -


—

trong đó: x0 là trục trung tâm.
• Nửa hình tròn:
y iL

4R
yc = — = 0,4244R.
3n

'

y

*T T

8

c

0

X

Hình 5

+ Bán kính quán tính:
/I
ly


\I p

+ Công thức chuyển trục song song của MMQT:
Jx = Jx + b2F

JY= Jy + a2F
J XY =

J xy +

a b F

Công thức trên ứng với trường hợp hệ xy là hệ trục
Hình 6

trung tâm của hình F.

Chương 5
XOẮN THUẦN TUÝ THANH THANG
+ Nội lực trên mặt cắt ngang Mz:
M >0
M|

m2

_________

M.<0


_________

CB o
Hình 7
Mỵ> 0 khi nhìn vào mật cắt thấy M, quay thuận chiều kim đồng hồ.

10


+ Tính mômen xoắn từ công suất:

w
M = 9550—
n

(Nm); W(kW); n(vòng/phút);

w
M = 7 02 9—
n

(Nm); w (mã lực); n (vòng/phút);

+ ứng suất trên mặt cắt ngang
M,

• Thanh mặt cắt tròn:

M,


w„

Thanh mật cắt chữ nhật:

M,

Tm a x

, , 2

ahb

^1 =y^ma>

’

x r ĩ T Ĩ Ĩ I T I Ụ Ĩ Ỉ T ỉ Tt x

í
Ằ
A

.

A

•

Hình 8
Hình 9


Các hẹ số cx, p và Y phụ thuộc tỷ số các cạnh b và h:
h/b

1

1,5

1,75

2

2,5

3

6

10

cc

a

0,208

0,231

0,239


0,246

0,258

0,267

0,299

0,313

0,333

(3

0,141

0,196

0,214

0,229

0,249

0,263

0,299

0,313


0,333

Y

1,000

0,859

0,820

0,759

0,776

0,753

0,743

0,742

0,742

Khi — > 10 có thế lấy (X = p = 0,333.
b
+ Biến dạng:
• Thanh tròn:
i: Thanh
1 nann co
có n ao;
đoạn:

JL 'í. M'

i=l ()

■Thanh chữ nhật:
bì
M,

e=|3Ghb

Hình 10

11


+ Điều kiện bền:

Tmax < [ĩ]

+ Điều kiện cứng:

9 max < [9]

+ Tính lò xo hình trụ bước ngắn:
M = P — Q = P;
2
^ D
_ 2
T max = T I + T 2

PD

p

0 ,2 d 3 + nd2

v 7ĩd

0 , 4d

4
Còn khi tính toán nếu kể đến các ảnh hưởng của lực cắt, độ cong của vòng dây, thì
thường sử dụng công thức sau:
D
trong đó k =
nd

Độ co (dan) của lò xo: X =

+ 0,25
D

-1

8PD3n p
G dậ
. = —; với c =
--- 201 là đô cứng của lò xo.
Gd

c
8D n

■T-, =■

Chương 6
UỐN PHẲNG
+ Nội lực trên mặt cắt ngang: Lực cắt Qy và mômen uốn Mx.
Dấu cúa nội lực: M x > 0 khi nó làm căng thớ dưới, Q > 0 khi nó làm phần xét quay
thuận chiều kim đồng hồ.
Qy > 0

Cách xác định nội lực: Sử dụng phương pháp mặt cắt.
12


+ Quan hệ vi phân giữa nội lực và tải trọng phân bố:

dz
Chú ỷ: Một số điểm cần nhớ khi vẽ biếu đồ nội lực:
- Nêu q là hàng sô' thì biểu đồ Q là hàm bậc nhất, biểu đồ M là hàm bậc 2 và nếu q có
chiếu di từ trẽn xuống dưới thì biểu đồ Q có chiều dốc từ trái sang phải, biểu đồ M có bể
lõm quav lên phía trên.
- Nếu q = 0 thì biểu đổ Q là hằng số, biếu đồ M là hàm bậc nhất.
- Tại mặt cắt nào đó có Q = 0 thì mômcn có giá trị cực trị (tiếp tuyến với biếu đồ M
lại mặt cắt này có phương nằm ngang).
+ Ung suất trên mặt cắt ngang:
• Úng suất pháp

với hình c h ữ nhật:

y xn

6

với hình tròn:

• ứiig suất tiếp:
• úhg suất c h ín h và phương chính tại một điểm:

tga max

ơ max
13


+ Điều kiện bền:
. Theo ứng suất pháp:

ơ max < [ơ]K

ơn ,^ W N
• Theo ứng suất tiếp:

I m.ix < [x]

• Theo thuyết bền:
TB3:

ơ„3

<[ơ]

ơ u4 = ^ a ; + 3 x ị < [ơ]

TB4:

Chương 7
CHUYỂN VỊ CỦA DẦM c h ị u u ố n
+ Các thành phần chuvển vị:
dy
2 thành phần chuyên vi là đô võng y và góc xoay (p'= —
đz
1
—= —
p EJX

+ Đô c o n g cua truc dầm khi bi uốn:

+ Phương trình vi phân đường đàn hổi của dám:
d 2y _

Mx

d z2 ~~

EJ

EJ gọi là độ cứiig chống uốn của dầm.
+ Xác định đường đàn hổi của dầm: 3 phương pháp:

/) Phương pháp tích pliân khôìii> xác dịnlì:
M,
(p= J _ M ĩ . ddz
z + cC :: vV = jI fI-- ^ d z dz + Cz + D
J EJ
CT
• J J EJ

c và D là 2 hằng số tích phân được xác định từ các điều kiện biên của dầm.
2)

Phươniị pháp thôn li s ố ban dầu:

Phương trình độ võng cúa đoạn thứ i+1 theo đoạn thứ i:
y j...l (z) = y, ( z) + A y i, + AOa( z - a ) - ^ [ K M M i. , ( a ) - K iM i ( a ) ] . - - ~ í l -

hJ

- ^P[JK ^ Q
^ U O - K . Q I. C
a ) ] . Ẩ ^I - - i 7 [ K ,.1q M ( a ) - K ,*q11| ( a ) l.( / ~ a)
I- 1 - 1 - 1
- 1
1

14


Với EJ là độ cứng quv ước (chắng hạn EJ = HịJ,) và ký hiệu:

^ L = K. •
E J

E

EJ
J

- Y
i+l

Nếu các đoạn đểu có EJ = const thì:
y i+1(z) = y i(z) + Aya +A 0 a( z - a ) - ^ - . ^ ^ — ^ p ( z ~ a)
EJ
2!
EJ
3!
\5
Aqa (z -a )4 Aq; (z-a )5
EJ
4!
EJ
5!
3) PhươìiíỊ pỉìáp đồ ìtìún (phương piiáp lải trụng giả)
, ,
,
M
,
,,
Cường đô của tải trong giả tao: q . = — — đãt lên dấm giả thì chuyến vi góc xoay (p

EJ
lại mật cắt nào đó sẽ tương đương với lực cắt giả tạo Q gt, còn độ võng y sẽ tương đương
với mômen giả tạo M gl.
Bảng 1. Sơ đồ các dầm thật và dầm giả tạo
Dầm thật

i A ...................... 777777/

Dầm giả tạo

■"Tj?
7777/

=0
Qtl * 0

rù> z

y =0
0*0

M k, = 0

M sl=0

Qg. *■0

Qg, * 0

A | ------------------------------- B

A ------------------------------- ^ R
Ku

y =0
0=0

M ,= 0
Q„ = 0

y*0
0*0

y =0
0*0

c

y = 0 y^O
0 ^0 0 ^ 0

,,

y# ũ y = ũ
0 * 0 0^0

.

n

y=0 y 0
0*0 0*0

M sl* 0
Q „ í0

AX T
M K1= 0

B ■ |c
M sl = 0 M ^ 0

Q„ . *0

Qgĩ* 0 Qg' * 0

c ^------- o------------ o--------R L>
*•
Ã
B
K
M g, * 0
QSr * °

M„, = 0
Q s’ * 0

= 0 M ul* 0
Q ^ o Qgr* 0

15


Một số trường hợp đáng nhớ:

i

A

A

/

Vb =

3EJ

tp -1

pứ
A

'q
B

Pa2 ( í + a)

Bf

48EJ

b

yc =

..

y ma . \

c

3ẼĨ

Bài toán kiếm tra độ cứng: y m.K < [y] hay:

trong đó [y] và

/

P f3

—

y

8EJ

..I
7 - 1.12

yc =

-V J
384E.I

qa
24EJ

<

lần lượt là độ võng tuyệt đối cho phép và độ võng tương đối cho phép.

Chưomg 8

CHỊU L ự c PHỨC TẠP
1. Uốn xiên
- Các thành phần nội lực trên mặt cắt ngang: M x và M y (trong
chương này thường bỏ qua ảnh hướng của lực cắt), với quv ước đầu:
M x > 0. M v > 0 khi các mômen này làm căng thớ dương của trục y,
X tương ứng, X, y là hệ trục quán tính chính trung lâm củ a mặt cắt.

Trên hình vẽ các mômen đều dương.
- ứng suất pháp trên mặt cắt ngang:
M.

M

J.

J„

ơ, = —- y + —

X

Hình 13

Trong công thức trẽn dấu của ơ z phụ thuộc dấư cùa M x , M v và dấu cúa toạ độ (x, >)
của điếm tính ứng suất. Cũng có thê tính theo còng thức kỹ thuật:
i
ơ , = ± J— —|yju± K
J— l—|x|
J.
Jy
16


Trong công thức trên lấy dấu của các số hạng bằng cách dựa vào phân vùng ứng suất.
Ví dụ trên hình 14, ứng suất tại A:
_A

KI , , M
J X

. X,

J y

M

M

1

a)
- Đường trung hoà và biểu đồ ứng suất:
+ Phương trình đường trung hoà: ơ 2 = 0
hay:

M

M

—— ■y + —-Í-- X = 0

JX
Rút ra:

với:

y=

J

y

M

J

M x

Jy

• X = tgp.x

tg p = -^ A
M v J„

Hình 15

4- Biểu đồ ứng suất pháp phảng có dạng tam giác, cách vẽ giống như vẽ biểu đồ ứng
suất trong uốn phẳng.
- Điểu kiện bền:
Với vật liệu dòn:
1m a x ơ 7k < [ơ ]k

[maxơ" < [ ơ ] n
Với vật liệu déo:

m a x I ơ l < [ơ]

2. T h a n h chịu uốn và kco (nén) đồng thòi
- Nội lực trên mặt cắt ngang: N z , M x và M y .
N z> 0 khi nó là ỉực kéo, còn dấu của mômen uốn như quy định ớ phần 1. Cũng có
thế trẽn mặt cắt ngang chỉ có N z và M x ; hoặc N z và My như trên hình 16.

17

-t-

h

z .y
A

1

t y

^

Hình 16
- ứng suất pháp trên mặt cắt ngang:
ơ7

N,

M

F

J x

J

1

_ M

~.y + — -.X
J.
J v

Trong công thức trên dấu của ơ z phụ thuộc dấu của N,, M x , M y và dấu của toạ độ
(x, y) của điểm tính ứng suất. Cũng có thc tính theo công thức kỹ thuật:
|n 1 |M j . . ỈM ị
ơz= ± - ^ ± ^ -U y ± ^ . X

F

Jx ựlJy 11

Trong công thức trên lấy dậu của CỊÚ' số Ị ìp g bằng cách dựa vào phân vùng ứng suát.
- Đường trung hoà và biểu đồ ứng suất:
+ Phương trình đường trung hoà: ơ , = 0
hay:

N,
F

ơ7 = — +

z

M
Mv _ n
—.y + — —.X = 0
J

Đường trung hoà là đường thẳng không đi
qua gốc toạ độ.
+ Biểu đồ ứng suất pháp phẳng có dạng
t X

tam giác, cách vẽ giống như vẽ biểu đồ trong
uốn xiên.
- Trường hợp riêng: Nén (kéo) lệch tâm:
Đó là trường hợp ngoại lực S0112 song với
trục thanh nhưng không đi qua trọne tàm mặt
cắt. Phương trình đường trung hoà có dạng:

a

18

b


với:

a=

và b =

ĨL

yK
Ý nghĩa củ a a, b và biểu đồ ứng suất như trên hình 17.

- Điều kiện bền:
+ Với vật liệu dòn:
j m a x ơ zk < [ơ]k

[ max ơ" < [ ơ ] n
+ Với vật liệu dẻo:

max I ơ I < [ơ]

- Lõi của mặt cắt ngang:
+ Định nghĩa:
Lõi của mặt cắt là một miền khép kín bao lấy tâm của mặt cắt sao cho khi điểm đặt
lực lệch tâm nằm bên trong hoặc nằm trên chu vi của miền đó thì trên mặt cắt ứng suất
chi có một dấu.
+ Cách vẽ lõi:
Đế xác định lõi của mặt cắt ta lần lượt cho các đường thẳng tiếp xúc với đường bao
chu vi của mặt cắt ngang mà không cắt mặt cắt và coi chúng ỉà các đường trung hoà của
mạt cắt. Chảng hạn ứng với đường trung hoà thứ i nào đó (ký hiệu là Aj), ta hoàn toàn có
ihc xác định được toạ độ của điểm đặt lực tương ứng Kj (xKi và y Kị) theo các hệ số 'àx và
b, của đường trung hoà đã cho như sau:
;2

:2
*x

XK,

— và y Kl =■
b;
a,

Nối tất cả các điểm đật lực Kị được xác định theo cách vừa nêu trên ta được chu vi loi
của mặt cắt cần tìm.
Ví dụ lõi của mặt cắt chữ nhật và mật cắt hình tròn cho trên hình 18.
b/2

b/2

ũi.
► X

a)

b)
Ilình 18
19


3. Thanh chịu uốn và xoán đồng thời
- Nội lực trên mặt cắt ngang: M x, M v và Mz.
- ứ n g suất pháp trên mặt cắt ngang:

M x, M y gây ra ứng suất pháp ơ z giống như trong uốn xiên.
M z gây ra ứng suất tiếp như trong chương xoắn. Ta phải xét riêng loại mặt cắt tr òn
và mặt cắt chữ nhật.
4. Trường hợp chịu lực tổng quát
Là tổng của các trường hợp trên.

Chương 9
DẦM TRÊN NỂN ĐÀN HỚI

1. Định nghĩa
Dầm đặt trực tiếp trên nền gọi là dám trên nén đàn hổi. Trong chương này chỉ irìinh
bày dầm trên nền Winkler với phản lực nền:
Po = k..y
trong đó:
p(1 - phản lực của nên tại điểm xét (N/rrr);
y - độ lún của nền tại chính điểm xét (m);

k,, - hệ số nền (N/m3).
Nếu gọi b là chiều rộng của dầm thì cường dộ phản lực nền được viết là:
p = ky với k = k0.b
Hộ số nên k,, cho trong bảng 2.
Bảng 2. Hệ sô nền k0
Đặc tính chung của nền

Tên đất nền

Hệ số nền k0(MN/rr')

1

2

3

Đất có độ chặt kém

Đất chảy
Đất mới đắp

1-5

Đất sét ướt và mềm nhão
Đất Có độ chật trung bình

Sỏi đắp (nhân tạo)
Đất sét ẩm

20

5 -10


/
ỉ)â chật

2

3

Sạn,sỏi

L/1
o
■I5
o

Cát đầm chặt

Đá dăm

Đất sét có độ ẩm bé
Đâ rất chặt

Đất sét pha cát dầm kỹ

1 0 0 -2 0 0

Đất sét cứng
Nề cứng

Đá mềm có vết nứt

200 -ỉ- 1000

Đá vôi
Đá dá sa thạch
Né- rất cứng

Đá rất rắn

Nể- nhân tạo

Nền cọc

Nểí từ vật liệu xây dựng

Gạch

4000 * 5000

Đá xây

5000 - 6000

Bê tông và bẽ tông cốt thép

8000-í- 15000

o

L/ì
o
•I-

1000- 15000

_ Tính dầm trên nền đàn hồi YVinkler
Phưưng trình vi phân đường dàn hổi củii dầm trên nền đàn hồi:
y lv(Z) + 4 m\ y ( Z) = - ^
n r
với m = ỉ —— có thứ nguyên là m4;
V4EJ
q - cường độ của lực phàn bô tác dụng lên dầm;
EJ - độ cứng chống uốn của dầm.
Phương trình đường đàn hồi của dầm:
v(z) = c m/(Cị cosm z + C 7 sinmz) + e"mi' (Cs cosm z + C 4s i m z ) - ^ ^ k
tioiíỉ đó: c ,, C2. c ;, c là các hằne sỏ tích phân được xác định từ các điều kiện biên của
từn bài toán cụ thế.
ư phưons trình đường đàn hồi, dựa vào các mối liên hệ vi phân của dầm chịu uốn dể
dàrỊ có thể xác dịnli được nội lực trong dầm.

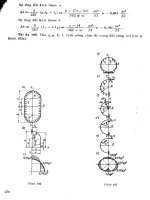
Bài toán dám dài vô hạn:
lét mội dầm (rên nền đàn hổi dài vô hạn chịu lực tập trung p như trên hình 19.
21


1r
a)

ìm ầ w M

y /m ỂI m m ấ m Ê ế ấ
I

3 71

b)
ìxrPm

y(
c)

'*-m ] I I I LU-*"

2k

^ fĩílM lT ĩỉW
' N
.

7T,Ĩ

; 4m
4m

dì

—- r n T ì ! l-)\

ÍTTTt^.

—

' / Jĩ

i i i l i i i r * ' ©
nL
L_______Z
111

^-rm m iirm -1-^
i-y^trrnTĩĩTĩTrn-r^^,
—

Hvl )
w

i4m
m

n
2m """*

e)

m ITmxu-LJ-

^mTl 11!n 1rr>w

í
m

Hình 19
Chuyển vị và nội lực của dầm:
Pm

Pm 2

2k

k

yU) =■— n ; 0U) = — — Th
p
p
M(zì = - — r|| Q(z) = -T-T|2
4m
2
với ký hiệu các hàm:

r| = e ~mz (cos mz + sin m z)
TỊI = e rri' ' ( c o s m z - s i n m z )

ĩ]2 = e„mz cosmz
TỊ-, = e"mz sin mz
Chú ý: Các hàm số r|, rịp r|2, rị., có thế tính trực tiếp bằng máy tính hoặc tra bảng điã
lập sẵn ở cuối cuốn sách này.
Các biểu đồ biểu diễn độ võng, góc xoay, mômen uốn và lực cắt của dầm được v/ẽ
trên hình 19b, c, d, e. Từ các biểu đồ này ta đưa ra các nhận xét sau đây:
+ Tại mặt cắt đặt lực tập trung p thì độ võng, mốmen uốn và lực cắt đạt giá trị cụíc
đại bằng:

22


Pin

M

^2k~
p
=
4m
p

Qmax

+ Các biểu đồ trên đều có dạng tuần hoàn tắt dần theo thời gian với chu kỳ T =

2n
m

71

Thật vậy, tại mặt cắt cách gốc toạ độ o một nửa chu kỳ z = — thì độ võng chỉ còn bằng
m
4% độ võng lớn nhất, tại mặt cắt cách gốc toạ độ o một chu kỳ z = — thì độ võng chỉ
m
còn bằng 0,2% độ võng lớn nhất và có thể coi như bằng không.
Có thế rút ra kết luận rằng dầm được coi là dài vô hạn nếu khoảng cách từ điểm dật
lực p đến các đầu mút của dầm lớn hơn — như trên hình 20. Nếu không thoả mãn thì
m
dầm không được coi là dài vô hạn.
Nếu dầm có nhiều lực tâp trung tác dụng thì ta phải dùng nguyên lý cộng tác dụng:
Phải giải bài toán dầm chịu từng lực rồi cộng các kết quả lại. Chú ý rằng với mỗi lực ta
phải chọn gốc toạ độ tại điểm tác dụng cua lực.
271
m

b>

a>—

i =

p„

271
m

om m ễS ễễẵ ẫ ễễẫ ễm ầ
yir

--------------- c --------------Hình 20

H ình 21

- Bài toán dầm dài bán võ hạn:
Xét một dầm dài bán vô hạn như trên hình 21. Chuyến vị và nội lực của dầm:

y(z) = V ì-(PoTl2 - mMoĩli)
k

2m 2
0(z) = ^ - ( - P oTi + 2 m M t,Ti2)
k
M(z) = — (-p„ri3 + mM0r|)
m

Q(z) = - P j l i - 2 m M 0ri3
23


- Dầm dài hữu hạn:
Xét một dầm dài hữu hạn chịu [ực như trên hình 22. Các phương trình chuyển vị và
nội lực của dầm:
y i+1(z) = y j(z) + ' Av + ^ k ì A .....
y'
k

-

m

mk

B m( z - u )

2T C m(M1- - f T DM,.a r i [ A q , + A q ; ( Z-a)]
fcj m~
bJm
K

7 7

A9 +

0i+|(z) = 0:(z) +

Aq'

T

ạ

EJm

p,.
HJm

M

A

Ay;,+

? '-'m (z-a)

M ]+1 (z) = M, (z) + Ma .Am(,-a,+

Aqa

P=.

1
Bm(/.i0+ - ^ - ( k A y a + Aqa ) Cm(z.a)
m
m

+ -Ịjlk A O a hAq:i)Drn(z.ll)
nr

Qi + |( z ) - Q i ( Z) +

+

m

P a A m( / - M) +

—

m

(ky,, + tló

) B m(/-a)

2 (kA0a + Aq', )Cm(z.a)- 4m M ;iD m(z.a)

với các hàm Crưlốp:
A m(z_;1)= chm(z-a). cosm(z-a)

Ịcosm(z-a).shm(/.-a) + sinm(z - a).chm(z-a)]

CmU..u= —shm(z-a).sinm(/-aj

4
24

[sinm(z-a).chm(/.-a) - cosm(z-a).shm(z-a)]


Hình 22
Các phương trình trên là các phương trình dạng truy hổi, ta có thể viết phương trình
cho đoạn đầu:
Y|(Z):

' \

y„+-

0,(z) = 0 .

M0
mz

bJm

/
M

+-

/

7 ~m z

p„
r,T

EJm

p

EJm

EJm

y„ + -

1

" m z

D„

q„+qỏ-z
k

q«

MI (7) - MưAm/ + — Bni/+ — 7 ( ky0 + q „ ) C1!ư+ — - ( kfì0 + q(,) D„
in
m
m
Q,(z) = PoA mz + — (kytl +q„) Bmz + - | r (k0o + q;,)C mz - 4mM 0D,
in
m
Chú ỳ: Các hàm Crưlốp có thể tính trực tiếp bằng máy tính hoặc tra bảng đã lập sẵn
ờ cuối sách này.

Chương 10
THANH CONG PHANG
1. Nội lực trên mặt cát ngang
Trường hợp tống quát có: Lực dọc Nz, lực cắt Q v và mômen uốn M x (hình 23).
2. Thanh cong chịu kéo (nén) đơn
+ Nội lực trên mặt cắt neang: Chỉ có một thành phđn là Nz.
+ úno suất trên mặt cắt ngang:
- N—/
ơ =
z

F
25


Biểu đồ phân bố ứng suất trên mật cắt ngang như hình 23, 24:

m y>0

N,>0

b)
Hình 23

3. Thanh cong chịu uốn thuần tuy phẳng
+ Nội lực trên mặt cắt ngang: Chỉ có mômen uốn Mx .
+ ứng suất trên mặt cắt ngang:
_M X
Sx

- ' o
•
và các ứng suât cực trị:

y
r+ y

M , y,
M x y7
ơ m;,Y= ——. — — - = —
s x r + y2 s x R 2

_

_ M V y,
min

c

s,

•

_ Mx

r + y,

o

y,
* n

s x R,

trong các công thức trên thì: r là bán kính cong của thớ trung hoà, được xác định từ
biểu thức:
(■

V

_

M — dF = 0
Fr+y
26


Cụ thế cho trong bảng 3.
Sx là inômcn tĩnh của mặt cắt đối với trục trung hoà:

s x = yc . F
(trong đó yc là. khoảng cách từ trọng tâm mặt cắt đến trục trung hoà x)
Rị = r + y, là bán kính cong của thớ gần tâm cong nhất.
R 2 = 1' + y2 là bán kính cong của thó' xa tâm cong nhất.
Ạy
^

m

a

x

)

Hình 25
Bảng 3. Công thức xác định bán kính cong của thớ trung hoà

27