D00 dạng toán khác về cực trị muc do 4
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (98.23 KB, 4 trang )
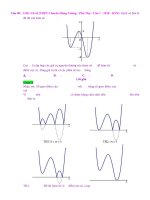
Câu 49: [2D1-2.0-4] (THPT Chuyên Hùng Vương - Phú Thọ - Lần 1 - 2018 - BTN) Hình vẽ bên là
đồ thị của hàm số
Gọi
.
là tập hợp các giá trị nguyên dương của tham số
điểm cực trị. Tổng giá trị tất cả các phần tử của
A.
.
B.
.
Chọn A
Nhận xét: Số giao điểm của
với
.
Vì
nên
đơn vị.
TH1:
. Đồ thị hàm số có
có
bằng
C.
Lời giải
với
để hàm số
.
D. .
bằng số giao điểm của
có được bằng cách tịnh tiến
điểm cực trị. Loại.
lên trên
TH2:
. Đồ thị hàm số có điểm cực trị. Nhận.
TH3:
. Đồ thị hàm số có điểm cực trị. Nhận.
TH4:
. Đồ thị hàm số có điểm cực trị. Loại.
Vậy
. Do
nên
.
Vậy tổng giá trị tất cả các phần tử của bằng .
Câu 48.
[2D1-2.0-4]
(Chuyên
Thái
,
điểm cực trị của hàm số
A. 2.
Nguyên
thỏa mãn
-
2018
,
-
BTN)
Cho
,
C. 3.
D. 5.
Lời giải
Chọn D
- Xét hàm số
.
Ta có:
.
Theo giả thiết, ta được
- Lại do:
.
nên
và
Do đó:
Hay hàm số
Khi đó đồ thị hàm số
có
có đồ thị dạng
có dạng
nghiệm phân biệt thuộc khoảng
số
. Tìm số
.
B. 1.
hàm
.
.
Vậy hàm số
Câu 44:
[2D1-2.0-4]
có
điểm cực trị.
(Chuyên Quang Trung - BP - Lần 4 - 2017 - 2018) Cho hàm số
có đồ thị
như hình vẽ và
với
. Đặt
. Có bao nhiêu giá trị của
để hàm số
có đúng hai
điểm cực trị?
A.
B.
C.
D.
Lời giải
Chọn C
Ta có
.
Đồ thị hàm số
có được bằng cách tịnh tiến đồ thị
Để hàm số
có đúng hai điểm cực trị thì
Dựa vào đồ thị suy ra
Câu 46:
[2D1-2.0-4] (THPT
Có bao nhiêu giá trị
có
A.
.
B.
hoặc
nên có
giá trị thỏa mãn.
Phan Chu Trinh - ĐăkLăk - 2017 - 2018 - BTN)
nguyên dương của tham số
để hàm số
điểm cực trị.
.
C.
.
D.
.
Lời giải
Xét hàm số
.
,
.
Ta có bảng biến thiên
đơn vị.
đổi dấu qua 2 điểm.
. Vì
Chọn B
Ta có
xuống dưới
Xét hàm số
Nên từ bảng biến thiên của hàm số
có
Do đó có
suy ra hàm số
điểm cực trị khi và chỉ khi
giá trị nguyên dương của tham số
có điểm cực trị.
để hàm số
.