Hat dien chuyen dong
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (251.58 KB, 6 trang )
r
r
r r
�
�
f
qE
q
v
Chuyển động của điện tích trong điện từ trường:
�.B �
Bài 1:
Một đi-ốt chân không phẳng (các bản cực là các bản phẳng),
khoảng cách giữa Anốt và Catốt là d = 2cm, được nối với nguồn điện
cao thế. Điốt nằm trong từ trường đều có cảm ứng từ B = 0,1T có
hướng vuông góc với mặt phẳng hình vẽ. Bỏ qua vận tốc ban đầu của
electron khi rời khỏi catốt.
Hãy xác định xem với hiệu điện thế đặt vào hai cực bằng
bao nhiêu thì electron có thể bay tới được anốt.
ĐS: U �3,5.105V
Bài 2:
Một hạt điện tích dương chuyển động phi tương đối tính trong miền có
điện trường và từ trường đều
r rvuôngr góc với nhau. Ở một thời điểm nào đó, vận
r
tốc của hạt bằng v0 ( v0 E ; v0 B ). Hỏi ở thời điểm véc-tơ vận tốc của hạt tạo
r
với véc-tơ v0 một góc 1800 và E = v0B thì độ lớn vận tốc của hạt bằng bao nhiêu?
ĐS: v 3v0
Bài 3:
Một hạt có khối lượng m, điện tích q dương, bắt đầu chuyển động với
vận tốc v theo hướng song song với trục ox trong một từ trường đều có cảm ứng
từ B= ax (x ≥ 0) (hình vẽ).
Hãy xác định độ dịch chuyển cực đại của hạt theo trục Ox.
y
+
B
vx
vy
vt
O
Bài 4:
Trong hình 8, S1 và S2 là hai mặt giới hạn nằm song song và
chia không gian ra làm ba phần khác nhau I, II, III. Trong các vùng I
và II có các từ trường đều, có phương vuông góc với tờ giấy, chiều
hướng ra ngoài, cường độ cảm ứng từ lần lượt là B 1 và B2. Trong vùng
III có điện trường đều cường độ E, chiều hướng từ S2 sang S1.
Người ta phóng một hạt nhỏ khối lượng m mang điện tích
dương q cho nó chuyển động với vận tốc v 0 từ O hướng về phía S1
L
khoảng cách từ O đến S1 là
bỏ qua tác dụng của trọng lực. Để cho
2
hạt có thể chuyển động theo quỹ đạo đó cho trong bài (2 đoạn cong
trên quỹ đạo có bán kính bằng nhau). Hãy xác định:
a) Tỷ số cường độ các cảm ứng từ B1 và B2.
b) Điện trường E phải có trị số nhỏ hơn bao nhiêu?
I
III
B1
S1
O
v0
S2
II
B2
Hình 8
Bài 5:
Một chùm prôtôn đi vào một vùng không gian có bề rộng d
= 4.10-2m và có từ trường đều B 1 = 0,2T. Sau đó prôtôn đi tiếp vào
vùng không gian cũng có chiều rộng d nhưng từ trường B 2 = 2B1.
Lúc đầu, Prôtôn có vận tốc vuông góc với véctơ cảm ứng từ
B và vuông góc với mặt biên của vùng không gian có từ trường
(hình 10).
a) Hãy xác định giá trị của hiệu điện thế V 0 để tăng tốc cho
prôtôn sao cho hạt prôtôn đi qua được vùng đầu tiên.
L
E
Chùm prtôn
r
B 1
ur
B2
d
d
Hình 10
x
b) Hãy xác định hiệu điện thế V 0 sao cho prôtôn đi qua được vùng thứ hai.
c) Hãy xác định hiệu điện thế V 0 sao cho prôtôn sau khi đi qua được vùng thứ hai, thì có vận tốc hợp
với phương của vận tốc ban đầu một góc 60 0.
Bài 6:
Một hạt có điện tích q > 0 và khối lượng m dịch chuyển trong
một môi trường trong đó hạt chịu một lực ma sát có dạng:
y
B
r
r
r
2v
với K > 0. Từ trường đều B không đổi vuông góc
F = - Kv
rv
với vận tốc v0 ban đầu của hạt. Chứng tỏ rằng chuẩn (độ lớn) của
v0
vận tốc hạt giảm theo thời gian. Vận tốc tốc bằng 0 có thể đạt được
sau một thời gian hữu hạn không?
Bài 7:
x
Hình 14
r
Một hạt mang điện tích dương q, khối lượng m chuyển động thẳng đều với vận tốc v0 dọc theo trục
x’Ox nằm ngang trong vùng không gian có tác dụng của điện trường đều và từ trường đều. Vectơ cường độ
r
r
điện trường E cùng chiều với trục Oz, hướng thẳng đứng xuống dưới (hình vẽ). Vectơ cảm ứng từ B vuông
góc với mặt phẳng hình vẽ.
r
1.Hãy xác định chiều và độ lớn của vectơ cảm ứng từ B
x
v0
O
(theo q, m, E và gia tốc rơi tự do g).
2. Khi hạt tới điểm O, người ta đột ngột đảo chiều của
B .
r
r
cảm ứng từ B (làm B đổi hướng ngược lại, nhưng vẫn giữ
vx
nguyên độ lớn ban đầu của nó). Chọn gốc thời gian là lúc hạt tới z
O. Hãy thiết lập phương trình chuyển động của hạt ở thời điểm t
FL
và phác hoạ quỹ đạo của hạt. Xem rằng thời gian làm đảo chiều
r
vz
v
của B là nhỏ không đáng kể.
P +Fđ
3. Xác định thời điểm gần nhất để hạt lại tới trục x’Ox.
Tìm vị trí của hạt và vectơ vận tốc của hạt lúc đó.
Bài 8:
z
Một chùm tia hẹp gồm các ion 39K và 41K đi vào khe hẹp
2α
của khối phổ kế, động năng của các ion là T = (500 �5) eV. Chùm
0
tia có góc mở là 2α = 6 khi bắt đầu đi vào khối phổ kế.
B
Từ trường B = 0,7T có phương vuông góc với mặt giấy. Đặt
tấm phim lên mặt phẳng AM (hình vẽ).
1. Các ion 39K và 41K với năng lượng 500eV, khi đi vào theo
A
N1 N2 M
phương vuông góc với AM, rơi vào hai điểm N 1 và N2 trờn tấm
phim. Hãy xác định các khoảng AN1; AN2 và N1N2.
2. Hãy xác định bề rộng của các vết trên phim ứng với từng
đồng vị. Muốn vậy, hãy tính:
a) Bề rộng D x1 của vết tạo ra do tính phân kỳ của chùm tia (tất cả các ion đều có năng lượng 500eV).
b) Bề rộng D x2 do sự khác nhau về ion. Cho biết tất cả các ion xuất phát từ A theo phương vuông góc
AM. Tổng chiều rộng các vết là D x �D x1 + D x2.
3. Liệu với khối phổ kế trên có thể phát hiện hai đồng vị 39K và 41K trong chùm tia trên không?
Bài 9:
Hai hạt mỗi hạt khối lượng m, được tích điện trái dấu nhưng có độ lớn bằng nhau. Ban đầu các điện
tích được giữ đứng yên trong từ trường đều có phương vuông góc với đường thẳng nối các điện tích. Sau đó,
hai điện tích được thả tự do cùng lúc. Hỏi ban đầu hai điện tích phải có khoảng cách L nhỏ nhất bằng bao
nhiêu để chúng không thể dính vào nhau sau khi được thả tự do. Bỏ qua hiệu ứng hấp dẫn.
Bài 10:
Một từ trường đều không đổi có cảm ứng từ B 0 hướng theo trục
x, một điện trường cũng có thành phần x và biến thiên điều hòa theo quy
luật E Ex E0 cos t . Một hạt có khối lượng m và điện tích q > 0
r
bay vào vùng của hai trường với vận tốc v0 vuông góc với trục x. Tính
khoảng cách cực đại từ hạt đến chỗ nó bay vào hai trường. Biết rằng tần
số góc của điện trường
ĐS: Lmax
qB0
. Bỏ qua tác dụng của trọng lực.
m
2mv0
E02
1 2 2
qB0
B v0
Bài 11:
Cho một tụ điện mà hai bản của nó là một phần của hai mặt trụ bán kính R 1=5cm, R2=6cm. Tụ điện
ur
được đặt trong từ trường đều có cảm ứng từ B = 0,2T và phương của B song song với trục chung của hai bản
tụ điện. Một chùm hạt α có năng lượng mỗi hạt W=1000eV, bay vào trong một tụ điện qua khe hẹp ở cách đều
hai bản tụ điện, biết rằng khi chuyển động hạt α luôn cách đều hai bản. Cho biết bản ngoài mang điện thế âm,
2 0l
C
R
điện dung của tụ điện
ln 2 , với l là chiều dài của các mặt trụ, hạt α có điện tích +2e và có khối lượng
R1
-27
mα =6,64.10 kg; bỏ qua hiệu ứng bờ ở các mép bản và tác dụng của trọng lực. Tính hiệu điện thế giữa hai bản
tụ.
ĐS: U=258V
Bài 12:
Máy phát điện từ thủy động (MHD: Magnetohydrodynamics). Tụ phẳng có diện tích mỗi bản là S,
khoảng cách giữa hai bản là d được đặt trong một dòng plasma dẫn điện có điện trở suất ρ. Plasma chảy với
r
ur
vận tốc v không đổi song song với hai bản. Hệ thống được đặt trong từ trường có B song song với hai bản
r
và vuông góc với v . Hai bản tụ được nối với điện trở R.
a) Giải thích tại sao tụ điện lại có tác dụng như một nguồn điện cung cấp dòng điện
không đổi cho R.
b) Với giá trị nào của R, công suất là cực đại? Tính giá trị cực đại này.
ĐS:
v 2 B 2 dS
d
a) b) Pmax
khi R
4
S
Bài 13:
Khoảng không gian giữa một cặp vật dẫn hình trụ đồng trục đã được rút chân không. Bán kính hình trụ
trong là a, bán kính hình trụ ngoài là b. Hình trụ ngoài gọi là anốt và có thể đặt ở điện thế dương V so với hình
ur
trụ trong. Người ta thiết lập một từ trường không đổi, đồng nhất (đều) B song song với trục hình trụ và
hướng vuông góc với mặt hình trụ như hình vẽ . Bỏ qua các điện tích cảm ứng trên các vật dẫn. Trong bài này,
ta nghiên cứu phương trình động lực học của êlectrôn khối lượng nghỉ m, điện tích –e, các êlectrôn này được
phát ra từ bề mặt trong của hình trụ.
ur
a) Thoạt đầu ta đặt điện thế V nhưng B =0. Các êlectrôn từ bề mặt trong của hình trụ
với vận tốc không đáng kể. Hãy tính tốc độ của nó khi đập vào anốt; cho kết quả trong hai
trường hợp: phi tương đối tính và tương đối tính.
Trong các phần còn lại của bài toán chỉ cần tính tới trườngurhợp phi tương đối tính.
b) Bây giờ cho V=0 và cho tác dụng của từ trường B . Một êlectrôn theo phương bán
uu
r
kính với vận tốc vo . Khi từ trường có giá trị một giá trị tới hạn Bc, êlectrôn không về được
anốt. Vẽ quỹ đạo của êlectrôn u
khi
r B hơi lớn hơn Bc. Từ đây về sau, ta cho tác dụng đồng thời
của V và từ trường đồng nhất B .
c) Từ trường sẽ gây cho êlectrôn một mômen động lượng đối với trục hình trụ khác
dL
không. Hãy viết một phương trình cho ta tốc độ thay đổi
của mômen động lượng. Chứng
dt
tỏ rằng phương trình này nói lên đại lượng (L-KeBr2) không thay đổi khi êlectrôn chuyển
động, trong đó K là một số xác định không có thứ nguyên, r là khoảng cách tính từ trục của
hình trụ. Xác định giá trị của K.
d) Xét một êlectrôn được phát ra từ hình trụ trong với tốc độ không đáng kể và không
đến được anốt, nhưng đạt được khoảng cách tối đa rm đối với trục hình trụ. Xác định tốc độ v
tại điểm mà khoảng cách theo phương bán kính là lớn nhất theo rm.
e) Chúng ta muốn dùng từ trường này để điều khiển dòng êlectrôn đi tới anốt. Với B>Bc
thì êlectrôn phát ra từ mặt trong của khối trụ với vận tốc không đáng kể sẽ không tới được
anốt. Xác định Bc.
f) Nếu êlectrôn được phát ra bằng cách đốt nóng khối trụ trong, thì chúng có thể
ur có vận
tốc khác không ở bề mặt khối trụ trong. Thành phần vận tốc ban đầu song song với B là vB,
ur
thành phần vuông góc với B là vr(theo phương bán kính) và vφ(theo phương vuông góc với
bán kính). Hãy xác định từ trường tới hạn để êlectrôn đạt tới anốt khi đó.
ĐS:
2
� mc 2 �
2eV u c 1 � 2
�
v
mc eV �
�
a)
m
b2 a 2
b) Quỹ đạo là một đường tròn bán kính R
2b
2
2
d
r
r
1
c) ( L eB ) 0 � L eB const K ; K
dt
2
2
2
2
2
eB(rm a )
d) v
2mrm
2b
2mV
2
b a
e
� 2
2b
2eV
2
v
v
v
f) Bc
�
r
m
e b2 a 2 �
e) Bc
2
a�
�
b�
Bài 14:
Xiclôtrôn là máy gia tốc gồm hai hộp rỗng bằng kim loại hình chữ D, cách nhau một khe hẹp. Có một
ur
từ trường với cảm ứng từ B không đổi vuông góc với bề mặt hộp. Gần tâm của 2 hộp có một nguồn phát ra
r
ur
điện tích với vận tốc v vuông góc với B . Biết khối lượng m và điện tích q của hạt.
a) Chứng minh rằng quỹ đạo của hạt trong từ trường là đường tròn. Tìm bán kính của
đường tròn này.
b) Có một hiệu điện thế xoay chiều đặt vào 2 hộp D với tần số thích hợp để tăng tốc
được hạt mỗi lần đi qua khe. Quỹ đạo của hạt gần giống đường xoắn ốc. Chính xác quỹ đạo ấy
có dạng như thế nào?
c) Tính tần số quay của hạt, cho nhận xét về tần số này. Tần số của hiệu điện thế xoay
chiều phải bằng bao nhiêu để hạt được tăng tốc mỗi lần đi qua khe? Trong phần dưới đây, xét
trường hợp gia tốc hạt prôtôn có mp=1,66.10-27kg, e=1,6.10-19C. Hiệu điện thế đặt vào D có tần
số f=107Hz. Vòng cuối cùng của prôtôn trước khi ra khỏi xiclôtrôn có bán kính 0,42m.
d) Tính cảm ứng từ B và động năng cuối cùng của prôtôn.
e) Cực đại của hiệu điện thế giữa các D là 20kV. Tính số vòng cuối cùng mà prôtôn đã
quay trước khi ra khỏi xiclôtrôn.
ĐS:
mv
qB
b) Trong không gian của mỗi nửa hộp thì quỹ đạo là nửa cung tròn, cung tròn ở nửa hộp sau
có bán kính lớn hơn cung tròn ở nửa hộp trước.
1
qB
c) f
= hằng số.
T 2 m
d) B 0,65155 T ;Wmax 3,6.108 eV
e) 9.107 vòng
a) R
Bài 15:
Dọc theo một ống thoát dài hình trụ bán kính R, người ta tạo ra một dòng electron ổn định, đối xứng
trục các e sẽ được gia tốc khi có hiệu điện thế U đi qua. Tìm sự phân bố mật độ e phụ thuộc vào bán kính r
trong một tiết diện ngang bất kì của dòng nếu kết quả đo từ trường theo hàm của r trong tiết diện này có dạng
q
�r �
B B0 � � với r < R và q >0 trong đó B0 và q là các hằng số. Xác định cường độ điện trường E theo r. Giả
�R �
thiết rằng các thông số của dòng electron không thay đổi dọc theo trục của nó.
c 1 q �r �
B0 � � ;
ĐS: n r
4 evR
�R �
q
c
2eU
�r �
E r .B0 .� � trong đó: v
là vận
v
m
�R �
tốc của electron
q 1
Bài 16:
Máy li tâm hoạt động như sau: Các Ion
có khối lượng khác nhau bay vào đầu của một
tụ trụ có bán kính ngoài r1 và bán kính trong r2.
Sau khi chuyển động theo đường tròn chúng
r
M
bay vào một từ trường B . Hỏi tỉ số giữa khối lượng và điện tích q của Ion bằng bao nhiêu
nếu nó bay qua máy li tâm khi hiệu điện thế giữa hai bản tụ là U còn bán kính quỹ đạo của nó
trong từ trường là RT ?
M RT2 B 2 r2
2 ln
ĐS:
q
cU
r1
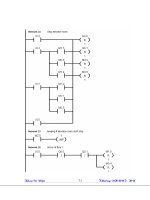
Bài 17:
r
Trong lòng một buồng hình xuyến có từ trường với cảm ứng từ B có độ
lớn B không đổi. Từ nguồn điểm P phát ra một chùm electron theo phương các
đường sức, electron đã được tăng tốc bởi hiệu điện thế V 0. Góc mở của chùm 20
rất nhỏ ( 20 << 1). P ở trên bán kính chính R của hình xuyến. Bỏ qua các tương
tác giữa các electron.
r
1. Để giữ chùm electron trong hình xuyến phải có một từ trường lái B1.
Tính B1 cho một electron chuyển động trên quỹ đạo tròn bán kính R.
2. Tính B sao cho chùm electron hội tụ ở 4 điểm cách nhau /2 như trong
hình. Khi xét quỹ đạo của electron thì có thể bỏ qua sự cong của các đường sức
từ trường.
3. Không thể giữ chùm electron trong hình xuyến nếu không có từ trường
r
20
R
P
Hình 20
lái B1. Nhưng electron vẫn có một chuyển động theo phương vuông góc với mặt phẳng của hình xuyến, gọi là
sự trôi (drif).
a) Chứng minh rằng độ lệch của bán kính quỹ đạo electron so với bán kính ban đầu R là hữu hạn.
b) Xác định chiều của vận tốc trôi
Chú thích: Có thể bỏ qua góc mở của chùm electron.
Sử dụng các định luật bảo toàn năng lượng và mômen động lượng.
Dữ kiện cho biết là
e
= 1,76.1011C / kg, V 0 = 3kV , R = 50mm
m