LỜI CAM ĐOAN

Tôi xin cam đoan những kết quả nghiên cứu trong luận văn là hoàn toàn
trung thực, của tôi, không vi phạm bất cứ điều gì trong luật sở hữu trí tuệ và pháp
luật Việt Nam. Nếu sai, tôi hoàn toàn chịu trách nhiệm trƣớc pháp luật.
TÁC GIẢ LUẬN VĂN

Nguyễn Tuấn Hải


LỜI MỞ ĐẦU
Trong thế giới hiện đại, cùng với sự bùng nổ về công nghệ, con ngƣời ngày
càng quan tâm đến các vấn đề nhƣ y sinh, địa chất học, viễn thám,…. Chính vì vậy
mà các phƣơng pháp xử lý ảnh, mà cụ thể hơn là xử lý biên ảnh và xử lý nhiễu ảnh
ngày càng cần thiết.
Trong những thập niên gần đây, biến đổi Curvelet-một dạng đặc biệt của
biến đổi Wavelet đang nổi lên nhƣ là những công cụ rất mạnh trong kỹ thuật xử lý
hình ảnh, đặc biệt trong lĩnh vực y sinh, viễn thám, quân sự, địa chất,…, do hiệu
quả của kỹ thuật này đối với xử lý nhiễu biên ảnh. Không chỉ ở các nƣớc phát triển
mà ở một số nƣớc đang phát triển gần chúng ta nhƣ Trung Quốc, Thái Lan, Ấn
Độ,... phép biến đổi Wavelet và Curvelet đang đƣợc nghiên cứu rất nhiều.
Trong khuôn khổ nghiên cứu của luận văn này, tôi xin phép đƣợc giới thiệu
những vấn đề cơ bản và ứng dụng điển hình trong kỹ thuật xử lý ảnh đa phân giảiảnh SAR sử dụng biến đổi Curvelet nhằm nâng cao chất lƣợng ảnh phục vụ cho
việc khai thác thông tin ảnh SAR trong các ứng dụng địa chất, quân sự...
Vì vậy, tôi quyết định chọn đề tài: “Xử lý ảnh Radar đa phân giải bằng
phương pháp curvelet ”, làm đề tài nghiên cứu cho luận văn tốt nghiệp.
Trong quá trình hoàn thành luận văn, tôi xin đặc biệt cảm ơn tới PGS.TS.
Nguyễn Thúy Anh. Tôi cũng gửi lời cảm ơn tới Ban giám hiệu Trƣờng Đại Học
Bách Khoa Hà Nội đã hỗ trợ, tạo điều kiện cho tôi trong thời gian học tập. Tôi xin
cảm ơn các bạn đồng nghiệp và ngƣời thân trong gia đình đã luôn động viên, khích
lệ tôi.

Hà nội, ngày 15 tháng 9 năm 2015
Học viên


TÓM TẮT NỘI DUNG LUẬN VĂN
Khử nhiễu ảnh, tăng cƣờng cấu trúc ảnh, là một trong những vấn đề đƣợc
nghiên cứu phổ biến và quan trọng nhất trong xử lý ảnh và tầm nhìn máy tính.
Hƣớng tới tác vụ khôi phục ảnh, nâng cao chất lƣợng ảnh phục vụ cho các quá trình
khai thác thông tin, xử lý thông tin trong các ứng dụng y khoa, viễn thám, địa
chất…. Đã đƣợc nghiên cứu ở nhiều nƣớc phát triển, Curvelet đã trở thành một
công cụ xử lý ảnh rất hiệu quả trong những năm gần đây.
Mục tiêu của nghiên cứu này là ứng dụng những ƣu điểm của Curvelet vào
xử lý ảnh SAR. SAR đã đƣợc áp dụng rộng rãi trong các vấn đề quân sự và lĩnh vực
dân sự nhƣ lập bản đồ, xác định mục tiêu tự động,…, vì độ phân giải cao của nó về
không gian, thời gian, hƣớng phƣơng vị. Tuy nhiên, ảnh SAR chịu tác động của
nhiễu đốm bội, một hiện tƣợng hỗn loạn là kết quả của sự kết hợp bƣớc sóng radar.
Sự tồn tại của nhiễu đốm bội ảnh hƣởng đến nhận thức và tầm nhìn máy tính, và các
kết quả xử lý thông tin từ ảnh SAR. Vì vậy, giảm nhiễu là quan trọng và cần thiết
cho các mục đích phát hiện mục tiêu, nhận dạng, và các hệ thống phân loại. Kỹ
thuật giảm nhiễu ảnh SAR điển hình có hai loại: một là các kỹ thuật xử lý đa tầm
nhìn trƣớc khi chụp ảnh và hai là các kỹ thuật lọc sau khi chụp ảnh. Các kỹ thuật xử
lý đa tầm nhìn gây ra các ảnh hƣởng không tốt, làm giảm độ phân giải của ảnh. Các
kỹ thuật sử dụng bộ lọc dựa trên thống kê cục bộ, đƣợc tính toán trong một cửa sổ
vuông cố định. Bằng cách này, nhiễu đốm giảm đi nhƣ là một chức năng của sự
không đồng nhất đƣợc đo bằng hệ số cục bộ của biến.
Nội dung nghiên cứu của đề tài:
CHƢƠNG 1. GIỚI THIỆU CHUNG VỀ ĐỀ TÀI
CHƢƠNG 2. GIẢI PHÁP XỬ LÝ ẢNH RADAR ĐA PHÂN GIẢI BẰNG
PHƢƠNG PHÁP CURVELET
CHƢƠNG 3. THỰC NGHIỆM, ĐÁNH GIÁ VÀ KẾT LUẬN



ABSTRACT
Image noise reduction, image enhancement structure, is one of the issues to
be studied popularly and the most important factor in image processing and
computer vision. Heading to restore image, improve images‟ quality for information
extraction process, information processing in medical applications, remote sensing,
geological .... Studied in many developed countries, curvelet became a very
effective tools for image processing in recent years.
The objective of this study is to apply the advantages of curvelet in SAR
image processing. SAR has been widely applied in military field and civil sectors
such as mapping, automatic target identification, ..., thanks to its high resolution in
space and time, the azimuthal direction. However, SAR images are affected by
multiple interference spot, a chaotic phenomenon as a result of a combination of
radar wavelengths. The existence of multiple spots interference affects cognition
and vision of computers, and the results of processing information from SAR
images. Therefore, noise reduction is important and necessary for the purpose of
target detection, identification, and classification systems. SAR image noise
reduction techniques typically have two kinds: one is the multi-processing
techniques before taking photos and the other is the masking technique after
shooting. Techniques for handling multiple views cause negative impacts such as
reducing the image resolution. The techniques using filters based on local statistics,
calculated in a fixed square window. In this way, interference spots decreases as a
function of the inhomogeneity is measured by local coefficient of variations.
Content of this study:
CHAPTER 1. AN OVERVIEW OF THIS STUDY
CHAPTER 2. SOLUTIONS TO PROCESSING RADAR MULTI-RESOLUTION
BASED ON CURVELET METHOD
CHAPTER 3. EXPERIMENTS, EVALUATION AND CONCLUSION



MỤC LỤC
LỜI CAM ĐOAN ........................................................................................................
LỜI MỞ ĐẦU ..............................................................................................................
TÓM TẮT NỘI DUNG LUẬN VĂN.........................................................................
ABSTRACT .................................................................................................................
MỤC LỤC ....................................................................................................................
DANH MỤC CÁC TỪ VIẾT TẮT ............................................................................
DANH MỤC CÁC HÌNH ẢNH .................................................................................
CHƢƠNG 1. GIỚI THIỆU CHUNG VỀ ĐỀ TÀI ................................................ 1
1.1 Nguyên lý radar ...............................................................................................1
1.1.1 Giới thiệu....................................................................................................1
1.1.2 Nguyên tắc .................................................................................................1
1.1.3 Ảnh radar ....................................................................................................4
1.2 Lý thuyết Wavelet ...........................................................................................7
1.2.1 Biến đổi Wavelet liên tục ...........................................................................8
1.2.2 Biến đổi Wavelet rời rạc ..........................................................................10
1.2.3 Wavelet và phân tích đa phân giải ...........................................................13
1.2.4 Phân tích gói Wavelet ..............................................................................15
1.2.5 Các họ Wavelet ........................................................................................19
1.2.6 Ứng dụng của Wavelet .............................................................................20
1.3 Lý thuyết Curvelet ........................................................................................20
1.3.1 Mối quan của Curvelet với Wavelet ........................................................21
1.3.2 Biến đổi curvelet ......................................................................................23
1.4 Mục đích đối tƣợng và phạm vi nghiên cứu của đề tài ..............................30
1.5 Phƣơng pháp nghiên cứu đề tài ...................................................................30
1.6 Ý nghĩa khoa học và thực tiễn của đề tài ...................................................31


1.7 Kết luận chƣơng ............................................................................................31

CHƢƠNG 2. GIẢI PHÁP XỬ LÝ ẢNH RADAR ĐA PHÂN GIẢI BẰNG
PHƢƠNG PHÁP CURVELET .............................................................................. 32
2.1 Các phƣơng pháp xử lý ảnh radar hiện nay ...............................................32
2.1.1 Những biến dạng hình học cơ bản của ảnh radar .....................................32
2.1.2 Phƣơng pháp xử lý hình học ảnh radar ....................................................35
2.2 Nhiễu và các phƣơng pháp xử lý nhiễu trên ảnh radar đa phân giải .....41
2.2.1 Nhiễu của ảnh radar .................................................................................41
2.2.2 Xử lý nhiễu trên ảnh radar - các loại phin lọc ..........................................42
2.3 Biểu diễn ảnh đa phân giải ............................................................................44
2.3.1 Các tiên đề của phân tích đa phân giải ................................................45
2.3.2 Biểu diễn Pyramid ..................................................................................47
2.3.3 Biểu diễn wavelet ....................................................................................50
2.4 Giải pháp xử lý ảnh radar đa phân giải bằng phƣơng pháp Curvelet ....60
2.4.1 Giới thiệu..................................................................................................60
2.4.2 Biến đổi Curvelet rời rạc nhanh (FDCT) .................................................60
2.4.3 Giảm nhiễu đốm trên ảnh SAR dựa trên FDCT.......................................62
2.5 Kết luận chƣơng ............................................................................................63
CHƢƠNG 3. THỰC NGHIỆM, ĐÁNH GIÁ VÀ KẾT LUẬN .......................... 64
3.1 Giới thiệu........................................................................................................64
3.2 Xử lý tín hiệu một chiều (1-D signal)...........................................................64
3.3 Xử lý ảnh 2D sử dụng Curvelet ...................................................................66
3.3.1 Khử nhiễu và khôi phục ảnh 2D ..............................................................66
3.3.2 Tách biên và khôi phục biên ....................................................................68
3.4 Xử lý ảnh radar đa phân giải bằng Curvelet..............................................69
3.4.1 Khử nhiễu và khôi phục ảnh SAR ...........................................................69


3.4.2 Tăng cƣờng cấu trúc ảnh SAR .................................................................71
3.5 Kết luận chƣơng ...........................................................................................72
KẾT LUẬN CHUNG .............................................................................................. 73

DANH MỤC CÁC KÝ HIỆU .................................................................................. 1
TÀI LIỆU THAM KHẢO ........................................................................................ 2


DANH MỤC CÁC TỪ VIẾT TẮT
Viết tắt

Tiếng Anh

Tiếng Việt

CCT

Continuous Curvelet Tranform

Biến đổi Curvelet liên tục

CWT

Continuous Wavelet Transform

Biến đổi Wavelet liên tục

DCT

Discrete Curvelet Transform

Biến đổi Curvelet rời rạc

DFT


Discrete Fourier Transform

Biến đổi Fourier rời rạc

DST

Discrete Shearlet Transform

Biến đổi Curvelet rời rạc

DWT

Discrete Wavelet Transform

Biến đổi Wavelet rời rạc

FDCT

Fast discrete Curvelet Transform

Biến đổi Curvelet rời rạc nhanh

FFT

Fast Fourier Transform

Biến đổi Fourier nhanh

FIR


Finite-Impulse Response

Bộ lọc có đáp ứng xung hữu hạn

FT

Fourier Transform

Biến đổi Fourier

IFFT

Inverse Fast Fourier transform

Biến đổi Fourier nhanh ngƣợc

LIDAR

Light Detection And Raging

MRA

Multi Resolution Analyzing

Dò tìm bằng ánh sáng và tập hợp
ánh sáng
Phân tích đa phân giải

PSNR


Peak Signal to Noise Ratio

Tỷ lệ tín hiệu trên nhiễu đỉnh

RMSE

Root Mean Square Error

Căn trung bình bình phƣơng lỗi

SAR

Synthetic Aperture Radar

Radar khẩu độ tổng hợp

UWT

Undecimated Wavelet Transform

Biến đổi Wavelet không phân rã

WPA

Wavelet Package Analyzing

Phân tích gói Wavelet

WT


Wavelet Transform

Biến đổi Wavelet


DANH MỤC CÁC HÌNH ẢNH
Hình 1.1 Hấp thụ và phản xạ sóng radio của địa hình ............................................5
Hình 1.2 Một số ảnh LIDAR chụp bề mặt địa hình ................................................6
Hình 1.3 Không gian và các không gian con trong đa phân giải ..........................13
Hình 1.4 Phân tích gói wavelet sử dụng các ký hiệu toán tử ................................16
Hình 1.5 So sánh biểu diễn trên mặt phẳng thời gian - tần số của Wavelet và gói
Wavelet .................................................................................................................16
Hình 1.6 Các nguyên tử gói Wavelet sinh ra từ Wavelet Daubechies 2 ...............17
Hình 1.7 Các họ Wavelet (a) Haar (b) Daubechies4 (c) Coiflet1 (d) Symlet2 .....19
(e) Meyer (f) Morlet (g) Mexican Hat ..................................................................19
Hình 1.8 Các phần tử của các wavelet( bên trái) và các curvelet với các tỷ lệ khác
nhau, các hƣớng và các chuyển dời trong miền không gian ( bên phải )..............21
Hình 1.9 Cửa sổ V(t) (trái) và W(r) (phải) ............................................................25
Hình 1.10 Cửa sổ

(bên trái) và hình chiếu đứng (bên phải) ........................25

Hình 1.11 Cửa sổ

(bên trái) và hình chiếu đứng (bên phải) .........................27

Hình 2.1 Khác biệt về kích thƣớc giữa cạnh gần và cạnh xa trên ảnh radar.........33
Hình 2.2 Sự nén đối tƣợng cạnh gần so với cạnh xa của ảnh radar ......................33
Hình 2.3 Hiện tƣợng co ngắn phía trƣớc...............................................................33

Hình 2.4 Hiện tƣợng chồng đè trên ảnh radar .......................................................34
Hình 2.5 Hiện tƣợng bóng trên ảnh radar .............................................................35
Hình 2.6 Ảnh hƣởng của chênh cao địa hình tới vị trí điểm trên thực địa............40
Hình 2.7 Sự tạo thành nhiễu trên ảnh SAR ...........................................................41
Hình 2.8 Mối tƣơng quan giữa độ lệch chuấn và giá trị trung bình cục bộ ..........42
Hình 2.9 Vị trí của một tín hiệu trong mặt phẳng thời gian-tần số đƣợc giới hạn
bởi định lý bất định Heisenberg. ............................................................................52
Hình 2.10 Những ví dụ về hàm wavelet mẹ và hàm scaling. Hàng thứ nhất: Haar.
Hàng thứ hai: Daubechie 6. Hàng thứ ba: trực giao 2.8. Hàng thứ tƣ: Meyer 8...53
Hình 2.11 A) Biểu diễn tín hiệu lấy mẫu trong miền thời gian B) Biểu diễn theo
biến đổi Fourier C) Biểu diễn theo cửa sổ Fourier D) Biểu diễn theo wavelet. ...53
Ad f
Hình 2.12 Phân rã một xấp xỉ rời rạc 2 j1 thành một xấp xỉ ở độ phân giải thô
D f
A2dj f
và tín hiệu chi tiết 2 ...............................................................................56
j


Hình 2.13 Tái tạo xấp xỉ rời rạc
chi tiết

D2 j f

A2dj1 f

từ xấp xỉ ở mức thô hơn

A2dj f


và tín hiệu

. .........................................................................................................57

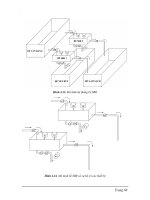
Hình 2.14 (a) Sử dụng phân đoạn W. (b) Sử dụng phân đoạn định hƣớng V ......62
Hình 2.15 Sơ đồ diễn tiến của khử nhiễu trên ảnh SAR dựa trên FDCT..............63
Hình 3.1 Biểu diễn tín hiệu 1D và nhiễu...............................................................64
Hình 3.2 Biểu diễn quy luật ngƣỡng của một vector ............................................65
Hình 3.3 Biểu diễn ngƣỡng cứng và ngƣỡng mềm ...............................................65
Hình 3.4 Biểu diễn khử nhiễu tín hiệu 1D ............................................................66
Hình 3.5 Kết quả khôi phục ảnh 2D sử dụng Curvelet .........................................66
Hình 3.6 So sánh chi tiết ảnh ban đầu và ảnh khôi phục ......................................67
Hình 3.7 Kết quả RMSE và PSNR trên ảnh 2D với Curvelet ..............................67
Hình 3.8 Kết quả RMSE và PSNR trên ảnh 2D với Wavelet ...............................67
Hình 3.9 Kết quả tách biên ảnh 2D sử dụng Curvelet ..........................................68
Hình 3.10 Kết quả khôi phục ảnh tách biên ..........................................................68
Hình 3.11 So sánh chi tiết ảnh tách biên và ảnh tách biên đƣợc khôi phục..........68
Hình 3.12 Kết quả RMSE và PSNR trên ảnh tách biên đƣợc khôi phục ..............69
Hình 3.13 Kết quả khử nhiễu và khôi phục ảnh SAR với Curvelet ......................69
Hình 3.14 So sánh chi tiết ảnh ban đầu và ảnh khôi phục ....................................70
Hình 3.15 Kết quả RMSE và PSNR giữa Curvelet và Wavelet ...........................71
Hình 3.16 Các cấu trúc ảnh khôi phục với Curvelet .............................................72


CHƢƠNG 1. GIỚI THIỆU CHUNG VỀ ĐỀ TÀI
1.1 Nguyên lý radar
1.1.1 Giới thiệu
Ra đa (phiên âm từ tiếng Pháp: radar) là thuật ngữ viết tắt của cụm từ tiếng
Anh: Radio Detection and Ranging (dò tìm và định vị bằng sóng vô tuyến) hay của
Radio Angle Detection and Ranging (dò tìm và định vị góc bằng sóng vô tuyến)

trong tiếng Anh. Đây là một hệ thống sử dụng để định vị và đo khoảng cách và lập
bản đồ các vật thể nhƣ máy bay hay mƣa.
Ảnh radar cung cấp nhiều thông tin về đất, nƣớc, rừng... Lần đầu tiên các nhà
khoa học dùng radar đặt trên vệ tinh để phát hiện nguồn nƣớc ngầm. Chi phí tìm
kiếm chỉ bằng 1% so với phƣơng pháp truyền thống chụp ảnh trên không.
Kỹ thuật này dựa trên nguyên lý: khi lớp đất, đá bên dƣới thấm nƣớc mƣa thì
bề mặt đất sẽ phồng lên, ngƣợc lại khi nguồn nƣớc ngầm nhiều, bề mặt đất sẽ bị lún
xuống. Những thay đổi trên có thể phát hiện và đo đƣợc bằng cách xem các ảnh
chụp một vị trí nhƣng tại các thời điểm khác nhau do radar khẩu độ tổng hợp (SAR)
thực hiện.
Đây là phƣơng pháp nhanh chóng và kinh tế mà các nhà khoa học Mỹ vừa
mới đƣa tìm ra. Họ dùng những hình ảnh có độ phân giải cao do SAR đặt trên các
vệ tinh của Cơ quan Hàng không châu Âu (ESA) chụp đƣợc để tìm ra những thay
đổi trên bề mặt đất. Kỹ thuật mày đã đƣợc ứng dụng chụp các vùng Bangkok (Thái
Lan), Thƣợng Hải (Trung Quốc) và Jakarta (Indonesia). Trƣớc đây, radar SAR mới
chỉ đƣợc sử dụng để theo dõi những thay đổi ở bề mặt đất, nhƣng chỉ nhằm phát
hiện đất bị lún.
1.1.2 Nguyên tắc
Trong kỹ thuật radar, ngƣời ta truyền đi một chùm xung vô tuyến có cƣờng
độ lớn và thu sóng phản xạ lại bằng máy thu. Bằng cách phân tích sóng phản xạ, vật
phản xạ đƣợc định vị, và đôi khi đƣợc xác định hình dạng. Chỉ với một lƣợng nhỏ
sóng phản xạ, tín hiệu radio có thể dễ dàng thu nhận và khuếch đại. Sóng radio có

[ Trang 1 ]


thể dễ dàng tạo ra với cƣờng độ thích hợp, có thể phát hiện một lƣợng sóng cực nhỏ
và sau đó khuếch đại vài lần. Vì thế radar thích hợp để định vị vật ở khoảng cách xa
mà các sự phản xạ khác nhƣ của âm thanh hay của ánh sáng là quá yếu không đủ để
định vị.

Tuy nhiên, sóng radio không truyền xa đƣợc trong môi trƣờng nƣớc, do đó,
dƣới mặt biển, ngƣời ta không dùng đƣợc radar để định vị mà thay vào đó là máy
sonar dùng siêu âm.
Sự phản xạ
Đặc trƣng vật lý cho khả năng mà một vật phản xạ hay tán xạ sóng radio là
diện tích phản xạ hiệu dụng.
Sóng điện từ phản xạ (tán xạ) từ các bề mặt nơi có sự thay đổi lớn về hằng số
điện môi hay hằng số nghịch từ. Có nghĩa là một chất rắn trong không khí hay chân
không, hoặc một sự thay đổi nhất định trong mật độ nguyên tử của vật thể với môi
trƣờng ngoài, sẽ phản xạ sóng radar. Điều đó đặc biệt đúng với các vật liệu dẫn điện
nhƣ kim loại hay sợi cacbon, làm cho radar đặc biệt thích hợp để định vị các máy
bay hay tàu thuyền. Các vật liệu hấp thụ radar, gồm có các chất có điện trở và có từ
tính, dùng trong các thiết bị quân sự để giảm sự phản xạ radar, giúp cho chúng khó
bị phát hiện hơn trên màn radar. Phƣơng pháp trong kỹ thuật sóng vô tuyến này
tƣơng đƣơng với việc sơn vật thể bằng các màu tối trong sóng ánh sáng.
Sóng radar tán xạ theo nhiều cách phụ thuộc vào tỷ lệ giữa kích thƣớc của
vật thể tán xạ với bƣớc sóng của sóng radio và hình dạng của vật. Nếu bƣớc sóng
ngắn hơn nhiều so với kích thƣớc vật, tia sóng sẽ dội lại tƣơng tự nhƣ tia sáng phản
chiếu trên gƣơng. Nếu nhƣ bƣớc sóng lớn hơn so với kích thƣớc vật, vật thể sẽ bị
phân cực, giống nhƣ một ăngten phân cực. Điều này đƣợc miêu tả trong hiện tƣợng
tán xạ Rayleigh (một hiệu ứng làm bầu trời có màu xanh lam). Khi 2 tia có cùng
cƣờng độ thì có hiện tƣợng cộng hƣởng. Bƣớc sóng radar càng ngắn thì độ phân
giải hình ảnh trên màn radar càng rõ. Tuy nhiên các sóng radar ngắn cần nguồn
năng lƣợng cao và định hƣớng, ngoài ra chúng dễ bị hấp thụ bởi vật thể nhỏ (nhƣ

[ Trang 2 ]


mƣa và sƣơng mù....), không dễ dàng đi xa nhƣ sóng có bƣớc sóng dài. Các radar
thế hệ đầu tiên dùng sóng có bƣớc sóng lớn hơn mục tiêu và nhận đƣợc tia phản hồi

có độ phân giải thấp đến mức không nhận diện đƣợc, trái lại các hệ thống hiện đại
sử dụng sóng ngắn hơn (vài xentimét hay ngắn hơn) có thể họa lại hình ảnh một vật
nhỏ nhƣ bát cơm hay nhỏ hơn.
Sóng radio phản chiếu từ bề mặt cong hay có góc cạnh, tƣơng tự nhƣ tia sáng
phản chiếu từ gƣơng cầu. Ví dụ, đối với tia sóng radio ngắn, hai bề mặt tạo nhau
một góc 90° sẽ có khả năng phản chiếu mạnh. Cấu trúc bao gồm 3 mặt phẳng gặp
nhau tại 1 góc, nhƣ là góc của hình hộp vuông, luôn phản chiếu tia tới trực tiếp trở
lại nguồn. Thiết kế này áp dụng cho vật phản chiếu góc dùng làm vật phản chiếu với
mục đích làm các vật khó tìm trở nên dễ dàng định dạng, thƣờng tìm thấy trên tàu
để tăng sự dò tìm trong tình huống cứu nạn và giảm va chạm. Cùng một lý do đó, để
tránh việc bị phát hiện, ngƣời ta có thể làm cho các bề mặt có độ cong thích hợp để
giảm các góc trong và tránh bề mặt và góc vuông góc với hƣớng định vị. Các thiết
kế kiểu này thƣờng dẫn đến hình dạng kỳ lạ của các máy bay tàng hình. Các thận
trọng nhƣ thế không hoàn toàn loại bỏ sự phản xạ gây ra bởi sự nhiễu xạ, đặc biệt
với các bƣớc sóng dài. Để giảm hơn nữa tín hiệu phản xạ, các máy bay tàng hình có
thể tung ra thêm các mảnh kim loại dẫn điện có chiều dài bằng nửa bƣớc sóng, gọi
là các miếng nhiễu xạ, có tính phản xạ cao nhƣng không trực tiếp phản hồi năng
lƣợng trở lại nguồn.
Phân cực
Sự phân cực thể hiện hƣớng dao động của sóng; với sóng điện từ, mặt phẳng
phân cực là mặt phẳng chứa vector dao động từ trƣờng. Radar sử dụng sóng radio
đƣợc phân cực ngang, phân cực dọc, và phân cực tròn tùy theo từng ứng dụng cụ
thể để định vị tốt hơn các loại phản xạ. Ví dụ, phân cực tròn dùng để làm giảm thiểu
độ nhiễu xạ tạo bởi mƣa. Sóng phản xạ bị phân cực phẳng thƣờng cho biết sóng
đƣợc dội lại từ bề mặt kim loại, và giúp radar tìm kiếm vƣợt trở ngại mƣa. Các sóng
radar có tính phân cực ngẫu nhiên thƣờng là cho biết bề mặt phản xạ nhƣ đất đá, và
đƣợc sử dụng bằng radar cho tàu bè.

[ Trang 3 ]



Hiện tƣợng nhiễu sóng
Hệ thống radar phải vƣợt qua một số nguồn sóng khác để tập trung trên mục
tiêu thật sự. Các sóng làm nhiễu bắt nguồn từ các nguồn bên trong và bên ngoài,
gồm chủ động và bị động. Khả năng vƣợt qua các sóng không mong đợi đƣợc định
nghĩa là tỉ số tín hiệu trên nhiễu (signal-to-noise ratio hay SNR). Trong cùng một
môi trƣờng nhiễu, tỉ số SNR càng lớn, thì hệ thống radar càng dễ định vị vật.
Sóng nhiễu
Sóng nhiễu luôn đƣợc phát ra kèm theo tín hiệu từ nội nguồn của sóng,
thƣờng gây ra bởi thiết kế điện tử không thực sự đồng bộ sử dụng các linh kiện điện
tử chƣa tối ƣu. Nhiễu chủ yếu xuất hiện nhƣ là sóng dội nhận đƣợc từ đầu thu vào
thời điểm thật sự không có sóng radar nào đƣợc nhận. Vì thế, hầu hết các nhiễu đều
xuất hiện ở đầu thu và các nỗ lực để giảm thiểu yếu tố này tập trung trong thiết kế
đầu thu. Để lƣợng hóa độ nhiễu, ngƣời ta đƣa ra chỉ số nhiễu, là tỷ số giữa cƣờng độ
sóng nhiễu thu đƣợc trên đầu nhận so với một đầu nhận lý tƣởng. Chỉ số này cần
đƣợc giảm thiểu.
1.1.3 Ảnh radar
Ảnh Rada có những đặc điểm khác biệt cơ bản so với ảnh quang học, đó là
năng lƣợng sóng điện từ do chính vệ tinh chủ động phát đến các vật thể trên bề mặt
trái đất, bƣớc sóng thƣờng đƣợc sử dụng nằm trong dải tần sóng vô tuyến cao tần (1
cm đến 1m). Hình ảnh của vật thể đƣợc thể hiện trên ảnh rada rất khác so với cảm
nhận của mắt ngƣời quan sát. Độ xám của ảnh phụ thuộc rất nhiều vào năng lƣợng
tán xạ ngƣợc của sóng siêu cao tần và các bóng thể hiện trên ảnh chỉ liên quan đến
góc tới của của sóng do vệ tinh phát ra. Ảnh rada có ƣu điểm là ít chịu ảnh hƣởng
của khí quyển, không lệ thuộc vào bức xạ mặt trời nên có thể thu đƣợc ảnh cả ngày
lẫn đêm và bƣớc sóng đƣợc sử dụng trong thu ảnh rada thƣờng đƣợc xác định trƣớc
và kiểm soát dễ dàng.
Viễn thám RADAR có một số đặc điểm:
 Hoạt động trong một dải sóng rộng từ band radio đến band cực ngắn (với


[ Trang 4 ]


bƣớc sóng từ micromet đến vài milimét);
 Có thể thu và phát các tần số radio phân cực theo cả chiều ngang lẫn thẳng
đứng;
 Đo đƣợc độ mạnh của backscatter (một phần năng lƣợng mà ăngten radar
nhận đƣợc và thời gian kéo dài giữa quá trình nhận và truyền tín hiệu);
 Do bƣớc sóng radio thƣờng dài hơn bƣớc sóng của ánh sáng nhìn thấy và ánh
sáng hồng ngoại nên chúng có thể xuyên qua đƣợc tán cây của lớp phủ thực
vật nên chất lƣợng ảnh RADAR không phụ thuộc thời tiết nhƣ ảnh viễn thám
quang học. Chƣa kể với những hệ thống RADAR có bƣớc sóng dài hơn có
thể xuyên qua lớp phủ bề mặt. Một số hệ thống RADAR có thiết bị có thể đo
đƣợc độ ẩm của đất;
 Cách thức tƣơng tác của các tín hiệu RADAR phụ thuộc vào kích thƣớc vật
thể, hình dạng, độ nhẵn bề mặt, góc tiếp xúc với các mức năng lƣợng sản
sinh từ sóng cực ngắn và hằng số điện môi;
 So với các hệ thống viễn thám khác, viễn thám radar ghi tƣ liệu trên cơ sở
của thời gian hơn là khoảng cách. Radar có thể ghi lại hình ảnh ở bƣớc sóng
dài hơn với độ phân giải cao hơn vì ở vùng sóng cực ngắn, sự hấp thụ và tán
xạ ánh sáng là nhỏ nhất. Thiết bị “chụp” ảnh RADAR có thể đặt trên máy
bay hay vệ tinh.

Hình 1.1 Hấp thụ và phản xạ sóng radio của địa hình
RADAR thƣờng đƣợc dùng để thành lập bản đồ che phủ đất, xác định cấu

[ Trang 5 ]


trúc thảm thực vật và lập mô hình số độ cao (DEM).

Các loại ảnh RADAR hay đƣợc dùng là RADARSAT, ERS, Envisat, Space
Shutle.
Gần đây còn có ảnh LIDAR (Light Detection And Raging, tạm dịch là dò
tìm bằng ánh sáng và tập hợp ánh sáng), cũng thuộc loại bộ cảm chủ động nhƣng sử
dụng sóng LASER
Ảnh LIDAR có một số đăc điểm:
 Sử dụng bƣớc sóng trong khoảng xanh biển đến cận hồng ngoại (from blue
to near- infrared).
 Đo khoảng cách giữa bộ cảm và đối tƣợng.

Hình 1.2 Một số ảnh LIDAR chụp bề mặt địa hình
 Có thể triển khai hệ thống quét (scan) và chụp ảnh.
 Có khả năng đo/ghi lại những tín hiệu phản hồi rời rạc, hệ thống hiện đại hơn
có thể đo/ghi lại toàn bộ các dạng sóng từ tín hiệu phản hồi.
 Sử dụng phổ biến trong thu thập thông tin về mô hình số độ cao (DEM), và
cũng có thể sử dụng để đo chiều cao và cấu trúc thảm thực vật.
Xử lý ảnh RADAR cũng nhƣ LIDAR cần có những phần mềm chuyên biệt,
khác với các phần mềm xử lý ảnh viễn thám quang học.
Về giá cả ảnh vệ tinh có thể dao động từ miễn phí đến hơn 100 USD/1 km2

[ Trang 6 ]


tuỳ theo thời gian cung cấp cũng nhƣ mục đích sử dụng ảnh.
Có rất nhiều công ty kinh doanh đƣợc phép bán ảnh. Ngƣời dùng cần thoả
thuận bản quyền quy định rõ cách thức sử dụng cũng nhƣ phân phối ảnh vệ tinh để
đƣợc phép sở hữu thông tin tối đa của ảnh cho hoạt động của mình.

1.2 Lý thuyết Wavelet
Ý tƣởng cơ bản của Wavelet là phân tích theo tỷ lệ. Các hàm Wavelet thoả

mãn các yêu cầu về mặt toán học đƣợc sử dụng để biểu diễn dữ liệu hay các hàm
khác.Ý tƣởng về phép xấp xỉ sử dụng các hàm xếp chồng đã tồn tại từ đầu thế kỉ 18
khi Joseph Fourier phát hiện ra có thể xếp chồng các hàm sin và cosin với nhau để
biểu diễn một hàm khác. Tuy nhiên, trong phân tích Wavelet, tỷ lệ đƣợc sử dụng để
phân tích dữ liệu theo một cách đặc biệt. Các thuật toán Wavelet xử lý dữ liệu theo
các tỷ lệ khác nhau hoặc các độ phân giải khác nhau. Khi quan sát tín hiệu với một
cửa sổ lớn, chúng ta sẽ nhận đƣợc các đặc điểm chung. Tƣơng tự, nếu chúng ta quan
sát dữ liệu với một cửa sổ nhỏ hơn, chúng ta sẽ nhận ra những đặc điểm chi tiết hơn.
Quy trình phân tích wavelet là chọn một hàm Wavelet nguyên mẫu, đƣợc gọi
là Wavelet phân tích (analyzing wavelet) hay Wavelet mẹ (mother wavelet). Phân
tích thời gian đƣợc thực hiện với dạng (version) co lại, tần số cao của Wavelet mẹ,
trong khi phân tích tần số đƣợc thực hiện với dạng giãn ra, tần số thấp của cùng
Wavelet mẹ. Vì tín hiệu nguyên bản hay hàm có thể đƣợc biểu diễn dƣới dạng một
khai triển Wavelet (sử dụng các hệ số trong tổ hợp tuyến tính của các hàm
Wavelet), các tính toán dữ liệu có thể đƣợc thực hiện sử dụng các hệ số Wavelet
tƣơng ứng. Và nếu nhƣ chọn đƣợc Wavelet phù hợp với dữ liệu, hay bỏ bớt các hệ
số dƣới một ngƣỡng nào đó, chúng ta thu đƣợc dữ liệu đƣợc biểu diễn rời rạc. Mã
hoá rời rạc (sparse coding) làm cho Wavelet trở thành một công cụ tuyệt vời trong
lĩnh vực nén dữ liệu.
Các lĩnh vực ứng dụng khác sử dụng Wavelet bao gồm thiên văn học, âm
học, kỹ thuật hạt nhân, mã hoá băng con, xử lý tín hiệu và xử lý ảnh, bệnh học thần
kinh, âm nhạc, ảnh cộng hƣởng từ (magnetic resonance imaging), quang học,
fractals, turbulence, dự báo động đất, radar, và các ứng dụng thuần tuý toán học nhƣ

[ Trang 7 ]


giải phƣơng trình vi phân từng phần (partial differential equation).
1.2.1 Biến đổi Wavelet liên tục
Biến đổi Wavelet liên tục (CWT) đƣợc định nghĩa:



W (a, b)   f (t ) * a ,b (t )dt

(1.1)



với a là hệ số tỷ lệ (scaling) và b là hệ số dịch (translation), với ψ*a,b(t)là liên
hợp phức của hàm wavelet ψa,b(t). Các phiên bản khác nhau của hàm Wavelet

 a ,b (t ) có thể thu đƣợc từ Wavelet cơ bản:


t b

 a 

1
2

 a ,b (t )  a  

(1.2)

với a, b là các số thực (a  0),  a ,b (t ) là hàm Wavelet gốc, có giá trị trung bình


bằng không:  (t )dt  0 . Hàm Wavelet  a ,b (t ) có dạng bất biến trong không gian



L2(R) của các hàm tích phân bình phƣơng vì có hệ số chuẩn hoá a



1
2

Tín hiệu có thể đƣợc khôi phục nhờ biến đổi Wavelet ngƣợc:
f (t ) 

1
C



 W (a, b)

a ,b

(t )



dadb
a2

(1.3)

trong đó C phải thoả mãn điều kiện:

ˆ ( )
C  
d  


2



(1.4)

với ˆ ( ) là biến đổi Fourier của hàm Wavelet  a ,b (t ) . C là hằng số phụ
thuộc vào hàm Wavelet  a ,b (t ) . C là hữu hạn chỉ khi hàm ˆ (0)  0 hay điều kiện
tƣơng đƣơng:


 (t )dt  0

(1.5)



Để chắc chắn rằng các hàm Wavelet phân rã nhanh chóng tới không và do vậy

[ Trang 8 ]


chúng đƣợc khu biệt rõ ràng trong miền thời gian, hàm Wavelet cần thoả mãn điều
kiện:



 (1  t



 t  dt  , > 0

(1.6)



Một chuỗi Wavelet có đƣợc nhờ gián đoạn hoá CWT. Sự gián đoạn hoá CWT
đƣợc thực hiện nhờ lấy mẫu trên mặt phẳng thời gian-tỷ lệ. Tốc độ lấy mẫu có thể
thay đổi theo sự thay đổi tỷ lệ với điều kiện không vi phạm tiêu chuẩn Nyquist. Tiêu
chuẩn Nyquist: tốc độ lấy mẫu tối thiểu cho phép tái xây dựng lại tín hiệu nguyên
bản là 2f, với f là tần số lớn nhất của tín hiệu[8]. Do vậy, khi tỷ lệ cao lên (tần số
thấp đi) tốc độ lấy mẫu có thể giảm nhƣ vậy số lƣợng phép tính giảm.

1.2.2.1 Tính tuyến tính
Tính chất tuyến tính của biến đổi Wavelet có tính chất tuyến tính của tích vô
hƣớng.

W f  g (a, b)   W f a, b    W g (a, b)

(1.7)

1.2.2.2 Tính dịch (translation)






W Du f (a, b)  W f (a, b  u)

(1.8)

Nhƣ vậy việc dịch tín hiệu ban đầu trong miền thời gian sẽ tƣơng ứng với dịch
trong biến đổi Wavelet liên tục.

1.2.2.3 Tính tỷ lệ (scaling)

W f (a, b)  W f (v




v

1

a, vb), f v t  

v f vt

(1.9)

Tính chất tỷ lệ làm cho biến đổi wavelet thực sự phù hợp để phân tích các cấu
trúc dạng bậc. Nó nhƣ là một kính hiển vi toán học với các đặc tính không phụ
thuộc vào sự phóng đại .


1.2.2.4 Tính bảo toàn năng lượng
Biến đổi wavelet liên tục cũng có tính chất bảo toàn năng lƣợng giống nhƣ
công thức Parseval của biến đổi Fourier.

[ Trang 9 ]


Định lý: Nếu hàm f (t )  L2 ( R) và có biến đổi Wavelet liên tục là Wf(a,b) thì:






1
f t  dt 
C
2

 

  W a, b
f

  

2

dadb
a2


(1.10)

1.2.2.5 Tính định vị (localization)
Biến đổi Wavelet liên tục có tính định vị tốt, đặc biệt là với những thay đổi
đột ngột trong miền thời gian ở tần số cao (hay tỷ lệ thấp), đây là một ƣu điểm so
với các phép biến đổi truyền thống.
1.2.2 Biến đổi Wavelet rời rạc
Vì những hàm Wavelet đƣợc định nghĩa đối với mọi điểm trong không gian
(a, b) nên rõ ràng việc áp dụng những cơ sở Wavelet rất dƣ thừa. Do vậy, để giảm
bớt sự dƣ thừa đó biến đổi Wavelet rời rạc (DWT) đƣợc giới thiệu[8]. Biến đổi
DWT dựa trên cơ sở mã hoá băng con, có thể đƣợc thực hiện dễ dàng, giảm thời
gian tính toán và tài nguyên yêu cầu.
Cơ sở của DWT đƣợc xây dựng từ năm 1976, khi các kỹ thuật phân tích tín
hiệu rời rạc đƣợc phát triển. Các nghiên cứu về DWT cũng đƣợc thực hiện trong
lĩnh vực mã hóa tín hiệu tiếng nói còn đƣợc gọi là mã hoá băng con (sub-band
coding). Năm 1983, các kỹ thuật tƣơng tự kỹ thuật mã hoá băng con đƣợc phát triển
đƣợc gọi là mã hoá hình chóp (pyramidal coding) và dẫn đến sơ đồ phân tích đa
phân giải (MRA).
Trong biến đổi Wavelet liên tục, tín hiệu đƣợc phân tích sử dụng một tập hợp
hàm cơ sở liên quan với nhau bởi hệ số tỷ lệ (a) và hệ số tịnh tiến (b). Trong DWT,
biểu diễn thời gian-tỷ lệ của tín hiệu số thu đƣợc nhờ sử dụng các kỹ thuật lọc số.
Tín hiệu đƣợc phân tích qua các bộ lọc với tần số cắt khác nhau ở các tỷ lệ khác
nhau.
Chúng ta có hàm rời rạc f(n) và định nghĩa biến đổi Wavelet rời rạc DWT đƣa
ra bởi:
C a, b   C  j , k    f n  j ,k n 
nZ

[ Trang 10 ]


(1.11)


với  j ,k là Wavelet rời rạc đƣợc định nghĩa:

 j , k ( n) 

1
2j

 n  2jk 
  2  j / 2 2  j n  k
j
 2




 



(1.12)

Các tham số a, b đƣợc xác định: a = 2j, b = 2j k.
Biến đổi DWT có thể biến đổi ngƣợc nếu nhƣ tập hợp tƣơng ứng của các mẫu
xác định một khung Wavelet:

A f


2

  f , a, b 

2

B f

2

(1.13)

a ,b

với A và B là hai hằng số dƣơng gọi là giới hạn của khung (framebounds).
Biến đổi ngƣợc đƣợc xác định nhƣ sau:

f n   C j, k  j ,k n

(1.14)

jZ kZ

Nếu giới hạn khung (framebounds) trong (1.13) là A=B=1, thì phép biến đổi
là trực giao.
Đây là tổng vô hạn theo cả chỉ số thời gian k và chỉ số tỷ lệ j. Tuy nhiên tổng
này có thể đƣợc tính hữu hạn với sai số rất nhỏ trong trƣờng hợp các hàm Wavelet
với toàn bộ năng lƣợng tập trung trong một khoảng nào đó, nhƣ vậy phép tổng hữu
hạn (1.14) theo k là đúng với một số xấp xỉ.

Để tìm hiểu tại sao phép tổng (1.14) theo j là hữu hạn với một số xấp xỉ, phần
tiếp theo của chƣơng sẽ đƣa ra khái niệm đa phân giải MRA. Khái niệm MRA đƣợc
phát triển bởi Mallat và Meyer, đây là nền tảng lý thuyết để xây dựng các Wavelet
sau này.
Tính chất biến đổi Wavelet
Wavelet đƣợc xác định bởi một số xác định các hệ số khác không M. Số hệ
số này đại diện cho số momen triệt tiêu (vanishing moments) đƣợc xác định nhƣ
sau: Nếu  x  là khả vi M lần và phân rã đủ nhanh, thì M-1 mômen Wavelet đầu
tiên triệt tiêu, nghĩa là:

dk
 x    tức là
dt k

 x  xdx  0 với 1  k  M
k

[ Trang 11 ]

(1.15)


Wavelet phải thoả mãn hai phƣơng trình tỷ lệ:

 x   2  hk  x  k 

(1.16)

k


 x   2   1k h k  1 x  k 

(1.17)

k

Ngoài ra, hàm tỷ lệ là trực giao với phép tịnh tiến của nó:

  x x  k dx  0

(1.18)

Và các Wavelet cần phải trực giao với hàm tỷ lệ của chính nó, ví dụ:

 x 2x  k dx  0

(1.19)

Các hệ số tỷ lệ phải thoả mãn điều kiện admissbility cũng nhƣ điều kiện trực
giao:
M

 hk  

 hk hk  2m   m

2

0m


k 1

(1.20)

k

có nghĩa rằng tổng trên là không với mọi m khác không. Một biểu thức quan
trọng khác, là hệ quả của điều kiện trên là:

 hn hn  2k   0

(1.21)

n

Nhƣ vậy, có thể kết luận rằng mọi tính chất của Wavelet đƣợc quyết định bởi
dãy h(k) và để biểu diễn sự phân tích và khôi phục Wavelet chúng ta chỉ cần các hệ
số của bộ lọc h(k).
Hàm tỷ lệ:

1,0  t  1
0, t  0,1

 t   

(1.22)

Hàm Wavelet mẹ:
1,0  t  1 / 2


 t    1,1 / 2  t  1
0, t  0,1


[ Trang 12 ]

(1.23)


1.2.3 Wavelet và phân tích đa phân giải
Định nghĩa: Không gian L2 = L2(R) là không gian của các tín hiệu tƣơng tự.
Phân tích đa phân giải MRA của L2 là một họ các không gian con V j  L2 R :
V2  V1  V0  V1  V2 

Các tính chất của họ không gian V j :
 V j  V j 1 , j  Z


V

nZ

n

 L2 và  nZ Vn  0

(1.24a)
(1.24b)

 f t   V j  f 2t   V j 1 , j  Z


(1.24c)

 f t   V0  f t  k   V0 , k  Z

(1.24d)

  t  k kZ xác định một cơ sở trực chuẩn cho V 0
(1.24e)
Nhƣ vậy họ  t  k , k  Z  tạo thành một cơ sở trực giao cho không gian
tham chiếu V 0 . Các không gian V j lồng vào nhau. Không gian L2(R) đóng kín tập
hợp mọi V j .

Hình 1.3 Không gian và các không gian con trong đa phân giải
Không gian L2 biểu diễn toàn bộ không gian. Vj biểu diễn một không gian
con, Wj biểu diễn chi tiết.
Hàm tỷ lệ  t  :

[ Trang 13 ]


Hàm  t  trong định nghĩa đa phân giải MRA đƣợc gọi là hàm tỷ lệ (scaling
function) hay hàm cha (father function) đôi khi còn đƣợc gọi là hàm xấp xỉ.

 j ,k t   2 j / 2  2 j t  k ,

j, k  Z

(1.25)


Với V j  span j ,k : k  Z .
Hàm  t  :
Hàm  t  đƣợc gọi là hàm Wavelet hay hàm mẹ (mother function).

 j ,k t   2 j / 2 2 j t  k ,

j, k  Z

(1.26)

Họ  j ,k : k  Z  tạo thành một cơ sở trực chuẩn cho Wn .
Theo định nghĩa đa phân giải, ta có phƣơng trình tỷ lệ:

 t   2  hk 2t  k 

(1.27)

k

Đặt không gian W j là phần bù của V j với V j 1 , V j 1  V j  Wj . Các hàm 

j ,k

là một cơ sở trực chuẩn của W j .
Với các tín hiệu thực tế có dải thông giới hạn, có một tỷ số j = J cho các hệ số
wavelet w j ,k là đủ nhỏ. Do đó có thể viết hàm f J  V J thành f J t   k s J ,kJ ,k t  .
Tƣơng tự nhƣ vậy hàm W j có thể đƣợc viết thành dạng d J t   k wJ ,k J ,k t  .
Tổng hợp lại, ta có:

f j  V J  V J 1  WJ -1  V J  2  W J  2  W J 1

   V j 0  W j0  W j 01    W J 1

(1.28)

và có thể viết:

f j  d J 1  d J  2    d j 0  f j 0


J 1

 w

j j0 k

 j ,k   s j 0,k  j 0,k , f J  V J

j ,k

k

với j0 là độ phân giải nhỏ nhất đƣợc chọn trong phân tích.

[ Trang 14 ]

(1.29)


Vì   W0  V1 , và  2t  k  là một cơ sở trực chuẩn của V1 ,  có thể đƣợc
viết thành:


 t   2  g k 2t  k 

(1.30)

k

đƣợc gọi là phƣơng trình Wavelet.
Các hệ số hk  và  g k  từ các phƣơng trình tỷ lệ và phƣơng trình Wavelet
tƣơng ứng với các bộ lọc thông thấp (xấp xỉ) và thông cao (chi tiết). Những bộ lọc
này đƣợc sử dụng trong thuật toán Mallat.
1.2.4 Phân tích gói Wavelet
Phân tích gói Wavelet (WPA) là sự khái quát hoá phân tích Wavelet cho
những thủ tục phân tích phức tạp hơn. Trong thủ tục phân tích Wavelet trực giao,
bƣớc chung là phân chia các hệ số xấp xỉ thành hai phần. Sau khi phân chia chúng
ta thu đƣợc vectơ của các hệ số xấp xỉ và vectơ của các hệ số chi tiết, cả hai ở tỷ lệ
thô. Thông tin bị mất giữa hai bƣớc xấp xỉ kế tiếp đƣợc giữ lại trong các hệ số chi
tiết.
Bƣớc tiếp theo bao gồm phân chia vectơ hệ số xấp xỉ mới, các chi tiết kế tiếp
không đƣợc phân tích lại. Theo trạng thái gói Wavelet tƣơng ứng, mọi vectơ hệ số
chi tiết cũng đƣợc phân tích thành hai phần sử dụng cùng phép tính gần đúng nhƣ
trong sự phân chia vectơ xấp xỉ. Điều đó dẫn đến phân tích phức tạp, cây nhị phân
đầy đủ đƣợc đƣa ra nhƣ trong hình 3.12. Sự so sánh giữa biểu diến trên mặt phẳng
thời gian-tỷ lệ của Wavelet và gói Wavelet đƣợc mô tả trong hình 3.13.
Các hàm cơ bản w n với n

ỉ số tần số danh định:

w n x  2  hk wn 2 x  k 


(1.31)

wn1 x  2  g k wn 2 x  k  n  0,1,2...

(1.32)

kZ

kZ

[ Trang 15 ]