Header Page 1 of 258.

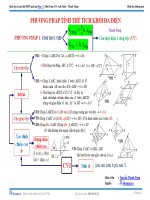
PHƢƠNG PHÁP PHẦN BÙ
TÍNH THỂ TÍCH KHỐI ĐA DIỆN PHỨC TẠP
Tác giả: Vương Thanh Bình
Bản Full đáp án tại Facebook: />Link video full miễn phí tại : />Mọi góp ý và bài tập liên quan đến phương pháp vui lòng Inbox Facebook
A-LÝ THUYẾT CHUNG
1) Khái niệm khối đa diện phức tạp : Là khối đa diện không cơ bản ( không phải chóp tam
giác, chóp tứ giác, hình lăng trụ, hình hộp, hình lập phương ... ) Hoặc cơ bản nhưng khó tính
chiều cao và diện tích đáy.
2) Ý tƣởng : Ta sẽ xây dựng khối đa diện phức tạp  H  nằm trong khối chóp cơ bản  A  . Ví
dụ dụ khối chóp  A  gồm khối đa diện phức tạp  H  và khối chóp cơ bản  B  khi đó
VH  VA  VB

3) Các dạng thƣờng gặp : +) Dạng 1: (Cơ bản) A  H  B  VH  VA  VB
+) Dạng 2: (Nâng cao) A  H  B  C  VH  VA  VB  BC
+) Dạng 3: (Sao) A  H  B  C  D  VH  VA  VB  VC  VD
4) Kiến thức liên quan :
4.1. Định lý Talet: Cho tam giác ABC , đường thẳng d song song với BC đồng thời cắt các
AM AN
cạnh AB, AC hoặc các đường kéo dài của 2 cạnh này tại M , N thì ta có tỉ lệ :

AB AC

4.2. Định lý 3 đƣờng giao tuyến: Cho 3 mặt phẳng  P  ,  Q  ,  R  giao nhau theo 3 giao tuyến
d1 , d2 , d3 thì 3 giao tuyến này một là đôi một song song hai là đồng quy.

Footer Page 1 of 258.


Header Page 2 of 258.

DẠNG 1: V H   V A  V B
Ví dụ minh họa: Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB  3a ,
4a
đáy nhỏ CD  a , cạnh bên AD  2a, BC 
. Chiều cao SA  3a . Tính thể tích của khối chóp
3
S. ABCD
A.

8a 3 2
3

B.

16a 3 2
9

C.

11a 3 3
9

D.

7a3 5
9

 Phân tích ý tƣởng
+) Để tính thể tích khối chóp S. ABCD ta phải tính được diện tích đáy ABCD là một

hình thang rất khó tính diện tích ( Vì không phải hình thang cân, không phải hình thang
vuông và chiều cao trong hình thang khó tính được )
+) Trong trường hợp này ta sẽ sử dụng phƣơng pháp phần bù tính thể tích
Ta xây dựng khối chóp S. ABCD nằm trong khối chóp S.IAB khi đó
V S . ABCD  V S .IAB   V S .ICD
Đương nhiên ta phải chọn sao cho khối chóp S.IAB và khối chóp S.ICD đều dễ dàng
tính được thể tích.

Footer Page 2 of 258.


Header Page 3 of 258.

 Giải
+) Kéo dài AD và BC cắt nhau tại I. Khi đó
1
V S . ABCD   V S .IAB   V S .ICD   SA.  S IAB  S ICD 
3
ID IC CD 1
1
8
+) Theo định lý Talet ta có:


  S ICD  S IAB hay S ABCD  S IAB
IA IB AB 3
9
9
4a
+) Từ AD  2a, BC 

dễ tính được IA  3a, IB  2a .
3
+) Theo định lý Herong ta có: SIAB 

p  p  IA p  IB  p  IC   2 2a 2

1
8
1
8
16 a3 2
Vậy VABCD  SA. SIAB  .3a. .2 2a 2 
3
9
3
9
9
BÀI TẬP TƢƠNG TỰ

Bài 1: Cho hình chóp S.ABCD có thể tích là a 3 đáy ABCD là hình bình hành tâm O. Mặt phẳng

 

qua AM và song song với BD cắt SB, SD tại E và F. Tính thể tích của khối đa diện AEMCB

Footer Page 3 of 258.


Header Page 4 of 258.


A.

a3
2 2

B.

a3
3

C.

a3 2
2 3

D.

5a 3
14

GIẢI

+) Ta xây dựng khối đa diện AEMCB nằm trong khối chóp S.ABC.
Khi đó: VAEMCB  VS . ABC  VS . AEM
+) Ta có:

VS . AEM SE SM 2 1 1
1

.

 .   VS . AEM  VS . ABC
VS . ABC SB SC 3 2 3
3

2
1
a3
 VAEMCB  VS . ABC  VS . AEM  VS . ABC  VABCD 
3
3
3
Bài 2: Cho lăng đứng ABC. A ' B ' C ' có đáy ABC là tam giác vuông cân, AB  BC  a cạnh bên
B'M B'N 1
AA '  2a . Gọi M và N là 2 điểm thỏa mãn sao cho

 . Tính thể tích khối đa điện
BA ' B ' C ' 3
B ' MNCBA

13a 3
9a 3 2
D.
27
28
GIẢI
+) Ta xây dựng khối đa diện B ' MNCBA nằm trong khối chóp tam giác I . ABC
V
1
26
IM IN IB ' 1 1 1 1

. .
 . . 
+) Ta có I .B ' MN 
 VIB ' MN  VIABC  VB ' MNCBA  VI . ABC
VI . ABC
IA IC IB 3 3 3 27
27
27
A.

a3
2

B.

4 3a 3
15

C.

1
1
1
1
a3
+) Mà VI . ABC  IB. BA.BC  .3a. .a.a 
3
2
3
2

2

Footer Page 4 of 258.


Header Page 5 of 258.

+) Vậy VB ' MNCBA 

26 a3 13a3
. 
27 2
27

Bài 3: Cho hình hộp chữ nhật ABCD. A ' B ' C ' D ' có AB  3a, AD  4a, AA '  3a . Gọi G là
trọng tâm tam giác CC ' D . Măt phẳng chứa B ' G và song song với C ' D chia khối hộp thành 2
V H 
phần. Gọi  H  là khối đa diện chứa C . Tính tỉ số
với V là thể tích khối hộp đã cho.
V

25a 3
A.
2

Footer Page 5 of 258.

57 a 3
B.
5


38a 3
C.
3

23a 3 3
D.
4


Header Page 6 of 258.
+) Khối đa diện  H  chứa C là: CMNABB '
+) Ta xây dựng khối đa diện  H  nằm trong khối chóp I . ABB '
Khi đó VH  VI .BB ' A  VICMN
1
1
1
1
+) Tính VI .BB ' A  IB. BB '.BA  .12a. .3a.3a  18a 3
3
2
3
2
V
8
19
38
+) Tính ICMN 
 VH  VIBB ' A  a3
VIBB ' A 27

27
3

DẠNG 2: V H   V A  V B  VC 
Ví dụ minh họa: [THPT THĂNG LONG 2016] Cho hình lập phương ABCD. A ' B ' C ' D ' cạnh a
có M và N lần lượt là trung điểm A ' B ', BC . Mặt phẳng  DMN  chia hình lập phương thành 2
phần. Khối đa diện đỉnh A kí hiệu là  H1  , phần còn lại kí hiệu là  H 2  . Tính tỉ số
A.

V H1 
V H 2 

2
1
37
55
B.
C.
D.
3
2
48
89
 Phân tích tƣ duy
+) Nhìn vào hình vẽ ta thấy mặt phẳng  DMN  chia khối lập phương thành 2 khối đa
diện trong đó khối đa diện  H1  là ABNDENF và phần còn lại
+) Khối đa diện  H1  cực kì phức tạp (không phải chóp, không phải lăng trụ, không phải
hộp...) nên việc tính toán là rất phức tạp
+) Để dễ tính ta sẽ sử dụng phƣơng pháp phần bù tính thể tích khối đa diện phức tạp
Ta sẽ đi xây dựng khối đa diện  H1  nằm trong khối đa diện dễ tính I . ADJ

Khi đó V H1   VI . ADJ  VIANE  VFBNJ

Footer Page 6 of 258.


Header Page 7 of 258.

 Giải
JB JN JF 1
IA ' IN IE A ' N 1


 và




JA JD JI 2
IA IJ ID
AJ
4
a
2a
a
Từ đó ta có thể tích được hết các đoạn thẳng ví dụ như: JB  ; BF 
, IA  ...
2
3
4
1

1 1
1 4a 1
4
+) Tính VIADJ  IA.S ADJ  IA. . AD. AJ  . . .2a.a  a 3
3
3 2
3 3 2
9

+) Theo định lý Talet ta có:

1 1
1 a 1 a a a3
+) Tính VIANE  IA. AE. AN  . . . . 
3 2
3 3 2 4 2 144
1
1
1 2a 1 a
a3
+) Tính VFBNJ  .FB. BN .BJ  . . . .a 
3
2
3 3 2 2
18
55 3
89 3
a  V H2   a3  V H1  
a
Vậy V H1   VI . ADJ  VIANE  VFBNJ 

144
144
V H1  55

Vậy
V H 2  89
BÀI TẬP TƢƠNG TỰ
Bài 1: Cho hình lăng trụ đều ABC. A ' B ' C ' cạnh đáy là a, cạnh bên là 2a . Gọi M và N lần lượt
là trung điểm của các cạnh B ' C ',C C ' . Mặt phẳng  AMN  chia khối lăng trụ thành 2 khối đa

Footer Page 7 of 258.


Header Page 8 of 258.

diện. Gọi  H  là khối đa diện chứa đỉnh B. Tính tỉ số

V H 
V

với V là thể tích của khối lăng trụ

đều.

a3
3

a3 3
4 2


7a3 2
15
GIẢI
+) Khối đa diện chứa đỉnh B là B'MEABCN (khối đa diện H )
+) Ta xây dựng khối đa diện H nằm trong khối chóp I.ABJ
Khi đó: VH  VI . ABJ  VI .EB ' M  VN . ACJ

A.

B.

C.

D.

23a 3 3
72

1
1
1
1 3a 3a3 3
+) Tính VI . ABJ  IB. BA.BJ sin 600  .3a. a. 
3
2
3
2 2
8

+) Theo công thức tỉ số thể tích thì


VIEB ' M
1 V
1
23
23a3 3
 , N . ACJ   VH  VI . ABC 
VIABC 27 VI . ABC 9
27
72

Bài 2: Cho hình lập phương ABCD. A ' B ' C ' D ' cạnh a. Gọi M và N lần lượt là trung điểm
1
A ' B ', A ' D ' và điểm P thỏa mãn CP  CC ' . Mặt phẳng  MNP  chia khối lập phương thành 2
4

Footer Page 8 of 258.


Header Page 9 of 258.
khối đa diện. Gọi  H1  là khối đa diện chứa đỉnh C'. Gọi  H 2  là khối đa diện còn lại. Tính tỉ
số

VH1
VH 2

25a 3
41 3
D.
a

96
155
GIẢI
+) Khối đa diện chứa đỉnh C ' là : PFB'MND'EC' là khối đa diện  H1 
A.

a3
4

B.

4a 3
25

C.

+) Ta xây dựng khối đa diện  H1  trong chóp P.C ' IJ
Khi đó: VH1  VP.C ' IJ  VE.D ' IN  VF .B ' MJ

1
1
1 3a 1 3a 3a 9a3
+) Tính VP.C ' IJ  PC '. CI .CJ  . . . . 
3
2
3 4 2 2 2
32
+) Theo công thức tỉ số thể tích thì: VE .D ' IN  VF .B ' MJ 

1

25
25a3
VP.CIJ  VH  VP.C ' IJ 
27
27
96

DẠNG 3: V H   V A  V B  VC   V D 
Ví dụ minh họa: Cho hình lập phương ABCD. A ' B ' C ' D ' cạnh a, có M và N là trung điểm của
A ' B ' và CD . Mặt phẳng   qua MN và song song với B ' D ' chia khối đa điện thành 2 phần.
Tính thể tích của khối đa diện chứa đỉnh A.
A.

a3
2

Footer Page 9 of 258.

B.

2a 3
3

C.

3a 3
5

D.


4a 3
7


Header Page 10 of 258.
 Phân tích ý tƣởng
+) Xác định thiết diện và ta xác định được khối đa diện chứa A là A'MJINFEBA (ta gọi
đây là khối đa diện H )
+) Đến dạng 3 thì chắc chúng ta đã quen với ý tưởng: Nếu tính thể tích 1 khối đa diện
phức tạp ta sẽ sử dụng phương pháp phần bù
+) Vậy ta sẽ xây dựng khối đa diện H nằm trong khối chóp tam giác S.APQ (dễ tính thể
tích) và V H   VS . APQ  VS . A' MJ  VE.BPF  VIDNQ

 Giải
+) Ta có V H   VS . APQ  VS . A' MJ  VE.BPF  VIDNQ
+) Sử dụng tính chất của quan hệ song song và định lý Talet ta dễ dàng tính được độ dài
các đoạn thẳng SA', A'J, ID....

1
1
1 3a 1 3a 3a 9a3
+) Tính VSAPQ  SA. AP. AQ  . . . . 
3
2
3 2 2 2 2
16
1
1
1 a 1 a a a3
+) Tính VS . A' MJ  SA '. A ' M . A ' J  . . . . 

3
2
3 2 2 2 2 48

Footer Page 10 of 258.


Header Page 11 of 258.

+) Tương tự VE .BPF  VIDNQ 

a3
48

+) Vậy V H   VS . APQ  VS .A 'MJ  VE .BPF  VIDNQ

a3

2

 Bình luận
+) Bài này còn 1 cách làm nhanh nữa là dựa và tính chất đối xứng của 2 khối đa diện tạo
thành bởi mặt phẳng   ta thấy thể tích của 2 khối đa diện này đều bằng nhau và bằng 1
nửa thể tích khối lập phương.
+) Do dạng này khá phức tạp nên ví dụ minh họa tác giả đã cố tính cho các bạn tỉ số rất
đẹp (toàn là trung điểm ) nên mới sinh ra cách đặc biệt kia.
+) Nếu các bạn muốn bài toán mang tính chất tổng quát hơn. Tác giả sẽ sửa lại vị trí điểm
thuộc cạnh A'D' như trong bài tập tự luyện số 2 thì bài toán sẽ căng thẳng hơn rất nhiều.
BÀI TẬP TƢƠNG TỰ
Bài 1: Cho hình lập phương ABCD.A'B'C'D' cạnh a. M, N là trung điểm A ' B ', CD . H là điểm

thuộc cạnh A ' D ' sao cho HA '  3HD ' . Mặt phẳng  HMN  chia khối chóp thành 2 đa diện.
Tính thể tích khối đa diện chứa điểm C.

a3
2

a3
2

a3
a3 2
D.
3
3
GIẢI
+) Khối đa diện chứa điểm C là CNFEB'C'D'HMG gọi tắt là hình  H 
A.

B.

C.

+) Ta có: V H   VJ .CIA  VJCNF  VGD ' IH  VEB ' MA
1
1
1 7a 1 7a 7a 343 3
+) Tính VJ .CIA  JC. CA.CI  . . . . 
a
3
2

3 4 2 4 6 576

1
1
1 3a 1 a 3a 3a3
+) Tính VJ .CNF  JC. CN .CF  . . . . 
3
2
3 4 2 2 4
64
+) Tương tự VE . AB 'M 

3a3
64

1
1
1 a 1 a a a3
. 
+) Tính VG.D ' HI  .GD '. .D ' I .D ' H  . .
3
2
3 4 2 4 6 576
 VEB MA
Vậy V H   VJ .CIA  VJCNF  VGD IH
'
'

Footer Page 11 of 258.


a3

2


Header Page 12 of 258.

Bài 2: Cho hình lập phương ABCD. A ' B ' C ' D ' cạnh a . Gọi M và N lần lượt là trung điểm của

D'E 5

. Mặt phẳng  MNE  chia khối lập phương thành 2
D ' D 12
khối đa diện. Gọi  H  là khối đa diện chứa đỉnh  C ' . Tính thể tích khối đa điện  H 
A ' B ', A ' D ' . E là điểm thỏa mãn

A.

a3
3

Footer Page 12 of 258.

B.

15a 3
37

154a 3
365

GIẢI

C.

D.

1549a 3
3600


Header Page 13 of 258.
+) Khối đa diện chứa đỉnh C' là EPCQFMND'C'B' (khối da diện H )
+) Ta có: VH  VK .C ' IJ  VK .CPQ  VE.D ' IN  VF .B ' MJ

1
1
1 5a 1 3a 3a 15a3
+) Tính VK .C ' IJ  KC '. C ' I .C ' J  . . . . 
3
2
3 4 2 2 2
32
1
1
1 a 1 3a 3a 3a3
+) Tính VK .CPQ  KC. CP.CQ  . .
. 
3
2
3 4 2 10 10 800

+) Tính VK .D ' IN

1
1
1 5a 1 a a 5a3
 .ED '. D ' I .D ' N  . . . . 
3
2
3 12 2 2 2 288

1
1
1 5a 1 a a 5a3
+) Tính VF .B ' MJ  FB '. B ' M .B ' J  . .
. 
3
2
3 12 2 2 2 288
Vậy VH  VK .C ' IJ  VK. CPQ  VE. D' IN  VF. B' MJ 

Footer Page 13 of 258.

1549a3
3600