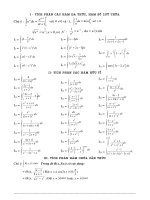Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

Phan Huy Chú- Khánh Xuân - BMT

TRẮC NGHIỆM ÔN KIỂM TRA 1 TIẾT CHƯƠNG TÍCH PHÂN
*NGUYÊN HÀM:
1) Tìm

∫( x

4

+ x3 + x 2 + x + 1) dx = ?

x 5 x 4 x3 x 2
+ + + + x+C
5 4 3 2
C. x 5 + x 4 + x 3 + x 2 + x + C
2
2) Tìm ∫ x ( x + 1) dx = ?

x5 x 4 x3 x 2
+ + + +x
5 4 3 2
D. 4 x 3 + 3 x 2 + 2 x + 1

A.

A. x 3 + x + C

B.

B.

1 4 1 2
x + x +C
4
2

C. 2x + C

 x3 + 2 x 2 + 3x + 4 
3) Tìm ∫ 
÷dx = ?
x2


1 2
4
x + 2 x + 3ln x − + C
A.
2
x
1 2
1
+C
C. x + 2 x + 3ln x −
2
4x
4) Tìm


∫(

B. 1 −
D.

)

D.

1 21 3

x  x + x ÷+ C
2 3


3 2
+ +C
x2 x

1 2
4
x + 2 x + 3ln x + + C
2
x

x + x3 + 3 x + 3 x 4 dx = ?

2 3 2 5 33 4 33 7
x +
x +

x +
x +C
3
5
4
7
1
3
1
4
+
x+
+ 3 x +C
C.
2 x 2
3 3 x2 3
5) Tìm nguyên hàm của hàm số y = 102 x
A.

10 x
102 x
B.
+C
+C
2 ln10
ln10
−x
3 x+2
+ 5x + 42 −7 x ) dx = ?
6) Tìm ∫ ( e + e

A.

2 3 2 5 33 4 33 7
x +
x +
x +
x
3
5
4
7
3 3 5 5 43 4 73 7
x +
x +
x +
x +C
D.
2
2
3
3
B.

C.

102 x
+C
2 ln10

D. 102 x 2 ln10 + C


1
5x 1 42 −7 x
1
5 x 1 4 2 −7 x
B. −e − x + e3 x + 2 +
− .
+C
− .
+C
3
ln 5 4 ln 7
3
ln 5 2 ln 4
1
5x 1 42 −7 x
1
5x 1 42−7 x
C. −e − x + e3 x + 2 +
D. −e − x + e3 x + 2 +
− .
+C
+ .
+C
3
ln 5 7 ln 4
3
ln 5 7 ln 4
1
1

3 
5 1
+
+
+
7) Tìm ∫  +
÷dx = ?
 x 4 x 3x − 8 1 − 2 x 6 − x 
1
1
1
A. 5ln x + ln 4 x + ln 3 x − 8 − ln 1 − 2 x − ln 6 − x + C
4
3
2
1
1
1
B. 5ln x + ln x + ln 3 x − 8 − ln 1 − 2 x − 3ln 6 − x + C
4
3
2
1
1
1
1
C. 5ln x + ln 4 x + ln 3 x − 8 − ln 1 − 2 x − ln 6 − x + C
4
3
2

2
1
1
1
D. ln 5 x + ln 4 x + ln 3 x − 8 + ln 1 − 2 x + 3ln 6 − x + C
4
3
2
A. −e − x + e3 x + 2 +


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
8) Tìm

x

∫ 1 + x dx = ?

A. x + ln 1 + x + C
9) Tìm

Phan Huy Chú- Khánh Xuân - BMT

x

∫ 1+ x

2

B. 1 − ln 1 + x + C


C. 1 + ln 1 + x + C

D. x − ln 1 + x + C

dx = ?

x2
+C
A.
1
x + x3
3

(

)

(

2
B. ln 1 + x + C

)

2
C. 2 ln 1 + x + C

D.


1
ln ( 1 + x 2 ) + C
2

1 + cos 4 x
dx là:
2
x 1
x 1
x 1
x 1
A. + sin 4 x + C
B. + sin 4 x + C
C. + sin 4 x + C
D. + sin 2 x + C
2 8
2 4
2 2
2 8
11) Nguyên hàm của hàm số y = x sin x là:
x
2
A. x s in + C
B. − x.cos x + C
C. − x.cos x + s inx + C
D. − x.s inx + cos x + C
2
1
12) Nguyên hàm của hàm số: f ( x ) =
là:

3x + 1
1
1
1
A. ln 3 x + 1 + C
B. ln 3x + 1 + C
C. ln ( 3x + 1) + C
D. ln 3 x + 1 + C
2
3
3
1
13) Nguyên hàm của hàm số: f ( x ) =
2 là:
( 2 x − 1)
10) Nguyên hàm của

A.

∫

−1
+C
2x −1

B.

−1
+C
2 − 4x


C.

∫

−1
+C
4x − 2

D.

−1

( 2 x − 1)

3

+C

2
14) Nguyên hàm sin x.cos xdx là:

A. cos 2 x s inx + C

B. sin 2 x.cos x + C

15) Tìm họ nguyên hàm của hàm số sau: y =

5x
5.2 x

−
+C
2ln 5 ln 2
2
1
−
+C
C. F ( x) = x
x
5 ln 5 5.2 ln 2
16) Nguyên hàm ∫ x ln xdx là:
3

3

1
.sin 3 x + C
12

D.

1
1
cosx − .cos3 x + C
4
12

2 x +1 − 5 x +1
10 x
5x

5.2 x
+
+C
2 ln 5 ln 2
−2
5
+ x
+C
D. F ( x) = x
5 ln 5 2 ln 2

A. F ( x) =

3

1
4

C. sin x −

B. F ( x ) = −

3

3

3

2
2

2
2
2
2
A. x ln x − 4 x + C B. 2 x ln x − 4 x + C
C. 2 x ln x − x + C
3
9
3
9
3
9
x
x
x
a sin − bx cos + C
3
3
17) ∫ x sin 3 dx =
Khi đó a+b bằng
A. -12
B.9
C. 12
2 x
2
x
18) ∫ x e dx = ( x + mx + n)e + C Khi đó m.n bằng
A. 0
B. 4
C. 6


3

3

2
2
D. 2 x ln x + 4 x + C
3
9

D. 6
D. −4


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
19) Tìm

∫ ( 7 x − 4)

5

dx = ?

6
6
A. . ( 7 x − 4 ) + C
7
20) Cho hàm số f ( x ) =


B.

( 7 x − 4)
6

( 7 x − 4) + C
C. 1 .
7
6

6

6

+C

D.

1
6
.( 7 x − 4) + C
7

1
. Chọn đáp án đúng:
(2 x − 1)2

1
+C
2 − 4x


A.

∫

C.

∫ f ( x )dx = 4 x − 2 + C

f ( x )dx =

Phan Huy Chú- Khánh Xuân - BMT

1

−1

B.

∫ f ( x )dx = (2 x − 1)

D.

∫ f ( x )dx = 2 x − 1 + C

3

+C

−1


21) (Đề thử nghiệm lần 2 BGD) Biết F ( x) là một nguyên hàm của của hàm số f ( x ) =

1
và F (2) =1 . Tính
x −1

F (3)
A. F (3) = ln 2 − 1

B. F (3) = ln 2 + 1

C. F (3) =

1
2

D. F (3) =

7
4

π 
÷.
2

22) Biết F(x) là một nguyên hàm của hàm số f ( x ) = sin ( π − x ) và F ( π ) = 1 . Tìm F 
A. 3

B. 2


C. 0

D. 1

x
và F ( π ) = 0 . Tìm F(x).
2
x
1
x 1
x
1
x 1
A. F ( x ) = 2sin + 2 B. F ( x ) = sin +
C. F ( x ) = 2sin − 2
D. F ( x ) = sin −
2
2
2 2
2
2
2 2
2
24) Biết F(x) là một nguyên hàm của hàm số f ( x ) = ( 1 + x ) và F ( 2 ) = 10 . Tìm F ( −1) .
23) Biết F(x) là một nguyên hàm của hàm số f ( x ) = cos

A. 0

B. 2


25) Gọi F(x) là nguyên hàm của hàm số f ( x) =
A. ln 2

B. 2 ln 2

C. -1

D. 1

1
thỏa mãn F(3/2)=0. Khi đó F(3) bằng
x − 3x + 2
C. − ln 2
D. −2 ln 2
2

26) Cho hàm số f ( x) = x − x 2 + 2 x − 1 . Gọi F(x) là một nguyên hàm của f(x), biết rằng F(1) = 4 thì
3

x 4 x3
49
− + x2 − x +
4 3
12
4
3
x
x
C. F ( x) =

− + x2 − x
4 3
A. F ( x) =

27) Cho hàm số y = f ( x ) có đạo hàm là f ' ( x ) =
A. ln2

B. ln3

x 4 x3
− + x2 − x + 2
4 3
x 4 x3
D. F ( x ) =
− + x2 − x +1
4 3
B. F ( x ) =

1
và f ( 1) = 1 thì f ( 5 ) bằng:
2x −1
C. ln2 + 1

D. ln3 + 1

2
28) Nguyên hàm của hàm f ( x ) =
với F ( 1) = 3 là:
2x −1
A. 2 2 x − 1

B. 2 x − 1 + 2
C. 2 2 x − 1 + 1
D. 2 2 x − 1 − 1
29) Nguyên hàm F ( x ) của hàm số f ( x ) = x + s inx thỏa mãn F ( 0 ) = 19 là:
A. F ( x ) = −cosx+

x2
2

B. F ( x ) = −cosx+

x2
+2
2


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

Phan Huy Chú- Khánh Xuân - BMT

x2
x2
D.
+ 20
F ( x ) = −cosx+ + 20
2
2
30) Cho f ' ( x ) = 3 − 5s inx và f ( 0 ) = 10 . Trong các khẳng định sau đây, khẳng định nào đúng:
C. F ( x ) = cosx+


A. f ( x ) = 3x + 5cosx+2

 π  3π
÷=
2 2

C. f ( π ) = 3π

B. f 

D. f ( x ) = 3 x − 5cosx+2

31) Hàm số f(x) = cos2x có nguyên hàm là:

1
sin 2 x + C
2
C. F ( x) = sin 2 x + C

1
2
F
(
x
)
=
−
sin 2 x + C
D.


A. F ( x ) =

B. F ( x ) = − sin 2 x + C

32) Hàm số nào sau đây là nguyên hàm của hàm số f(x) = (2x – 1)2

1
3
( 2 x − 1) + x + C
6
4 x3
1
D. F ( x) =
+ 2 x2 + x + + C
3
6

4 x3
1
− 2x2 + x − + C
3
6
1
3
C. F ( x) = ( 2 x − 1) − x + C
6

B. F ( x) =

A. F ( x) =


33) Nguyên hàm của hàm số f ( x) =

)

(

1
x2 + 1

là:

2
A. F ( x) = ln x + x + 1 + C

x

C. F ( x) =

x2 + 1

B. F ( x) = ln x 2 + 1 + C

+C

x3
+ x +C
3

D. F ( x) =


34) Một nguyên hàm của hàm số: y = cos5x.cosx là:

11
1

 cos 6 x + cos 4 x ÷+ C
26
4

11
1

C. F(x) =  sin 6 x + sin 4 x ÷+ C
26
4


1
sin5x.sinx +C
5
1  sin 6 x sin 4 x 
+
D. F(x) = − 
÷ +C
2 6
4 

A. F(x) =


35) Một nguyên hàm của hàm số: y =
A. F ( x) = x 2 − x 2 + C
C. F ( x) = −

1 2
x 2 − x2 + C
3

x3
2 − x2

B. F(x) =

là:

36) Một nguyên hàm của hàm số: f ( x ) = x 1 + x 2 là:

(

)

1 2
x 1 + x2 + C
2
3
x2
C. F ( x) =
1 + x2 + C
3
37) ∫ tan 2xdx = ?

A. F ( x) =

(

)

(
(

1 2
x +4
3
1 2
D. F ( x) = − x − 4
3
B. F ( x) = −

(

)
)

)

B.

2 − x2 + C

3
1

1 + x2 + C
3
3
1
D. F ( x) = x 2 1 + x 2 + C
3

B. F ( x) =

(

1
1
ln cos 2x + C
C. − ln cos 2x + C
2
2
2
2
38) Cho ∫ f ( x)dx = x − x + C . Khi đó ∫ f ( x )dx bằng
A. 2 ln cos 2x + C

2 − x2 + C

)

D.

1
ln sin 2 x + C

2


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
A.

2 3
x − x+c
3

Phan Huy Chú- Khánh Xuân - BMT

B. x 4 − x 2 + C

C.

x5 x 3
− +C
5 3

D.

x3 x 2
− +C
3 2

TÍNH NHANH NGUYÊN HÀM (TÍCH PHÂN) CỦA HÀM SỐ HỮU TỶ
1
1
x−a

dx =
ln
+C
Công thức 1: ∫
( x − a)( x − b)
a−b x−b
Công thức 2 :
Ví dụ :

∫x

1

mx + n

∫ ( x − a)( x − b) dx = a − b (ma + n) ln x − a − (mb + n) ln x − b  + C

2x −1
2x −1
dx = ∫
dx
( x − 1)( x + 2)
+ x −2

2


 2x −1 
2 −1 1
=

=
a = 
÷
x
+
2
1
+
2
3



2x −1
a
b
x =1
=
+
●Cách 1 : Ta có
. Nháp tìm a, b . Ta có 
( x − 1)( x + 2) x − 1 x + 2
2(−2) − 1 5
b =  2 x − 1 
=
=

÷

x − 1  x =−2

−2 − 1
3


1 1
2x −1
5 1 
1 1
5
1
1
5
dx = ∫  .
+ .
dx + ∫
dx = ln x − 1 + ln x + 2 + C
Vậy ∫ 2
÷dx = ∫
3 x −1
3 x+2
3
3
x + x −2
 3 x −1 3 x + 2 
●Cách 2 : Áp dụng nhanh công thức 2

∫x

2x −1
2x −1

1
1
5
dx = ∫
dx = 1.ln x − 1 + 5ln x + 2 + C = ln x − 1 + ln x + 2 + C
( x − 1)( x + 2)
3
3
3
+ x −2

(

2

)

2x −1
có nguyên hàm là :
x − x−6
A. F ( x) = ln ( x + 3)( x − 2) + C

39) Hàm số f ( x) =

C. F ( x) = ln

2

x+3
+C

x−2

D. F ( x) = ln

40) Nguyên hàm của hàm số : f ( x) =
A. −

1
+C
x −3

B. F ( x) = ln ( x − 3)( x + 2) + C

B.

41)
Nguyên hàm của hàm số :

1
x − 6 x + 9 là
2

1
+C
x −3

f (x) =

x−3
+C

x+2

1
x − 4x + 3

C. ln x − 3 + C

2

là :

D. - ln x − 3 + C .


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

A.

1 x −3
ln
+C
2
x −1

42) Tính nguyên hàm
A. ln

1
3


2

A. ln

2

x −2
+C
1
x−
2

44) Tính nguyên hàm

1 x−2
ln
+C
2
x −1

B.

∫ 2x

∫x

2
D. ln x − 4 x + 3 + C

C. ln


x−2
+C
x −1

D.

1 x+2
ln
+C
2
x +1

D.

2 x−2
ln
+C
3
x −1

1
dx
− 5x + 2
1 x −2
ln
+C
3 x −1

B.


C.

2
x−2
ln
+C
1
3
x−
2

2x + 3
dx
− x −2

2

A. 7 ln x − 2 − ln x + 1
C.

x −3
+C
x −1

C. ln

1
dx
− 3x + 2


x+2
+C
x +1

43) Tính nguyên hàm

1
x −1
ln
+C
2 x −3

B.

∫x

Phan Huy Chú- Khánh Xuân - BMT

1
7 ln x − 2 − ln x + 1
5

(

)

45) Tìm nguyên hàm của hàm số f(x) biết f ( x) =
A.


x 2 + 3x
+C
x 2 + 4x + 3

C.

1
( ln x + 1 + 3 ln x + 3 ) + C
2

B.

7
1
ln x − 2 − ln x + 1
5
5

D.

7
1
ln x − 2 − ln x + 1
3
3

2x + 3
x + 4x + 3
2


B. −

(x

x 2 + 3x
2

+ 4x + 3

)

2

+C

2
D. ( 2 x + 3) ln x + 4 x + 3 + C

*TÍCH PHÂN
4

46) (Đề thử nghiệm lần 2 BGD)Biết

∫x
3

S = a +b+c

B. S = 2


A. S = 6
a

47) Biết

∫
0

B. a = ln 2
1

∫ (e
48) Tính tích phân sau:
0

2

C. S = − 2

D. S = 0

x +1
dx = e . Giá trị của a là ?
x

A. a = e 2

A. 3

dx

= a ln 2 + b ln 3 + c ln 5 , với a, b, c là các số nguyên. Tính
+x

2

2x

+

3
)dx
x +1

B. 5

2

C. a = e

e2
+ a ln 2 + b
bằng
2
C. 7

2

D. a = ln 5
Giá trị của a+b là :
D. 9


2


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
49) Giả sử

π
4

∫ sin 3x.sin 2 xdx = (a + b)
0

A.

3
5

B.

Phan Huy Chú- Khánh Xuân - BMT

2 . Khi đó giá trị của a + b là
2

6
5

1
5


C.

D.

1
2

2

∫

2
50) Cho tích phân I = 2 x x − 1dx . Khẳng định nào sau đây sai:
1

3

A. I =

∫

2 32
C. I = u
3

2
27
B. I =
3


udu

0

3

D. I ≥ 3 3
0

2

51) Giá trị của

∫x

2

− 1 dx là

−2

A.2

B.4
2

52) Biết I =

D.3


xdx
1
= lnb . Chọn đáp án đúng:
2
+2 a

∫x

−1

A. ab=6

B. a =b
2

53) Biết I =

C.5

∫x

x

5

2

+1


0

dx =

C. 2a – b = 1

D. a>b

1
( 2ln a − b ) . Chọn đáp án đúng:
4

A. a - b = 13

B. a
C. a=3; b = 4

D. a - b=9

1

∫

5
2
54) Cho I = x 1 − x dx . Nếu đặt
0

1

A.

∫ t ( 1 − t ) dt

B.

0

∫e

55) Biết

3x

0

dx =

1

0

2

2

1 − x 2 = t thì I bằng :

∫ t ( 1 − t ) dt

C.

∫ t (1− t )

2 2

2

0

dt

D.

0

1

∫( t
1

4

− t 2 ) dt

e −1
. Tìm khẳng định đúng trong các khẳng định sau?
b
a

A. a = b

B. a < b

π
4

∫

56) I = x(1 + sin 2x)dx =
0

C. a + b = 10

π2 a
+ . Tích a.b là
32 b
B. −4

A. 4

D. a = 2b

D. −2

C. 2

π
2

∫

57) I = x 2 s inxdx . KQ là
0

A. π − 1

B. π − 2

C. π − 3

D. π − 4

π

a
3
58) Kết quả của I = ∫ x sin xdx có dạng π . Tích a.b là :
b
0
A.1

B.3
1

∫

2x
59) Kết quả của I = (x − 2)e dx có dạng

0

C.6

a + be2
. Kết quả a + b là
4

D. 12


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
A. 8

Phan Huy Chú- Khánh Xuân - BMT

B. 2

C. 7

D. 3

C. 10

D. −10

1

b
−x

60) I = ∫ ( 2x + 1) e dx = a + . KQ a.b là
e
0
A. −15

B. 15
e

∫

61) Kết quả của I = x ln x dx có dạng
1

A. 3

a + be2
. Tổng a + b là
4
C. −1

B. 0

D. 2

2

62) Kết quả của I = ∫ (x − 2) ln x dx có dạng a ln 2 + b . Kết quả tích a.b là
1

A.

5
2
e

B. −



C.

5
4

D. −

5
4

D. −

e2
+1
2

3
÷ln xdx KQ là
x

∫

63) I =  2x −
1

A.

5
2

e2
+1
2

B.

e2
−1
2

C. −

1
− ln 2
2

C.

e2
−1
2

1

2
64) I = ∫ x ln(1 + x )dx KQ là
0

1
A. − − ln 2
2

B.

1
+ ln 2
2

1
D. − + ln 2
2

2

ln x
a + b ln 2
dx có dạng
. Tổng a + b là
3
x
16

1

65) Kết quả của I = ∫
A. 0
66) I =

B. 6

π /4

x

∫ 1 + cos 2 x dx

C. 5

D. 1

KQ là

0

1π
2
A. −  + ln
÷
2 4
2 ÷

3

67) Biết tích phân

B.

1

∫9+ x

2

π
2
+ ln
4
2

C.

π
2
− ln
4
2

D.

1π
2
 + ln

÷

2 4
2 ÷


dx = aπ thì giá trị của a là

0

A.

1
12

B.12

C.

1
6

D.6

π
2

68) Tính tích phân sau: (2 x − 1) cos xdx = mπ + n . Giá trị của m + n là:

∫

0

B. −1

A. 2
69) Tính tích phân sau:

e 3

∫1 x

ln 2 xdx =

C. 5
4

b
ae + b
.Giá trị của
là:
a
32

D. −2


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

−1
A. 32

1
B. 32
2

70) Giá trị của tích phân I = ∫
1

A. 5

Phan Huy Chú- Khánh Xuân - BMT

−1

3

C. 5

D. 32

2 x2 − x + 2
dx có dạng a + b 2 + c ln 2 . Tổng a+b+c là
x
D. 1

C. −5

B9
4

71) Tích phân I =

∫

16 − x 2 dx có giá trị có dạng I = aπ + b . Giá trị a+b là

0

A. 2

B. 8
2

∫x

72) Tính I =

0

A.

C. 4

D. 1

2x − x 2 dx có giá trị dạng I = π + b . a + b có giá trị là:
a c
c

14

3

B.

29
4

C.

7
2

D. 2

3

1
dx = a ln 2 + b ln 3 . Tính S = a + b .
−x
2
A. S = 1
B. S = 0
C. S = 2
1
3
x dx 1
= ln 2 . Tìm a để biểu thức trên đúng.
74) Cho biểu thức ∫ 4
x +1 a
0

∫x

73) Biết

2

A. a = 3

B. a = 2

C. a = 1

B. I= −1

C.I=3

D. S = −2

D. a = 4

75) (Đề thử nghiệm lần 2 BGD)Cho hàm số f ( x ) có đạo hàm trên đoạn [ 1; 2] , f (1) =1 và f (2) = 2 . Tính
2

I = ∫ f '( x)dx .
1

A.I=1

D. I =

7
2
3

76) Cho hàm số f(x) có đạo hàm trên đoạn [0;3], f(0) = 2 và f(3) = −7 . Tính I =

∫ f ' ( x ) dx .
0

A. 3

C. −5

B. -9

77) (Đề thử nghiệm lần 2 BGD)Cho
A.I=32
78) Biết

2

0

0

C.I=16
1

0

0

D. 9

∫ f ( x)dx = 16 . Tính I = ∫ f (2 x)dx

B.I=8

3

D. I=4

∫ f ( x ) dx = 12 . Tính I = ∫ f ( 3x ) dx .

A. 3

B. 6
2

79) Biết

4

4

C. 4

D. 36

C. 2

D. 16

 x

∫ f ( x ) dx = 8 . Tính I = ∫ f  2 ÷ dx .
1

2

A. 12

B. 4
4

80) Nếu f(x) liên tục trên đoạn [0; 4] và

2

∫ f (x)dx = 4 thì ∫ f (2x)dx có giá trị là
0

A. 4
81) Tìm hàm số

y = f ( x)

B. 2
biết rằng

0

C. 1

f '( x ) = 2 x + 1 và f (1) = 5

D. 8


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
A. f ( x ) = x 2 + x + 3
82)

Tìm hàm số

Phan Huy Chú- Khánh Xuân - BMT

B. f ( x) = x 2 − x + 3

y = f ( x)

C. f ( x) = x 2 + x − 3

7
3
C. f ( x) = 2 x 3 + x − 3 D. f ( x) = x 3 − x − 3

2
biết rằng f '( x ) = 2 − x và f (2) =

A. f ( x ) = x 3 + 2 x + 3 B. f ( x) = 2 x − x 3 + 1
83) Tìm a>0 sao cho

∫

a

0

A. a = 2

x

xe 2 dx = 4
B. a = 1

4

84) Kết quả tích phân

∫x

2

3

C. a = 3

B. 2 ln 4 − 3ln 3 − ln 2

D. 2ln 4 + 3ln 3 − ln 2
5

∫x

2

4

A. 2ln 3 + 3ln 2
86) Tính tích phân sau:

∫

12

10

A. 35

1
dx bằng:
− 3x + 2
B. 2ln 3 − ln 2
(

131
54
e

∫

C. 12

1 − ln x
x2

1

0

0

B.

1

∫ (1− u) e

−u

0

du

C.

0

∫ ( 1− u ) e du

u

D.

1

e

∫x

88) Nếu đặt t = 3ln 2 x + 1 thì tích phân I =

1

2

D. 2

dx thành:

1

ln x
3ln 2 x + 1

1 1
B. I = ∫ dt
21t

∫ ( 1− u ) e

2u

du

1

dx trở thành:
e2

4

1
A. I = ∫ dt
31

D. ln 3 − 3ln 2

2x +1
a
) dx = ln Khi đó a+b bằng
x + x−2
b
B.

∫ ( 1− u ) du

C. 2ln 3 − 3ln 2

2

87) Đổi biến u = ln x thì tích phân
A.

D. a = 4

x −3
dx bằng:
− 3x + 2

A. 2ln 3 − 3ln 2
C. 2ln 3 + 3ln 2
85) Kết quả tích phân

D. f ( x) = x 2 − x − 3

e

1 t −1
dt
D. I = ∫
41 t

2
C. I = ∫ tdt
31
1

5
2

89) Nếu đặt u = 1 − x thì tích phân I = ∫ x 1 − x dx trở thành:
2

0

1

∫ (

)

2
A. I = u 1 − u du
0

∫

2
2
C. I = u 1 − u
0

1

π
4

2

4

2
B. I = ∫ ( t − 1) dt
31

91) Nếu đặt x = 2sin t , tích phân

∫
0

dx
4 − x2

2

0

du

∫( u

D. I =

4

1

− u 2 ) du

6 tan x
dx trở thành:

3 tan x + 1

2

1

)

∫ cos x
0

1
2
A. I = ∫ 2t dt
30

∫ (

B. I = u ( 1 − u ) du

90) Nếu đặt t = 3 tan x + 1 thì tích phân I =
1

1

0

thành:

3

C. I =

∫
1

2 2
( t − 1) dt
3

3

D. I =

4

∫ 3 t dt
0

2


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

A.

π
6

∫ dt

B.

0

Phan Huy Chú- Khánh Xuân - BMT

π
6

∫ tdt

C.

0

π
6

dt
t
0

∫

D.

∫ dt
0

92) Nếu đặt t = sin x thì tích phân
A.

π
3

bằng

B.

C.
π
2

93) Đổi biến u = s inx thì tích phân

∫ sin

4

D.

x cos xdx thành:

0

1

∫

A. u 4 1− u 2 du

B.

0

π
2

1

C.

∫ u du
4

∫ u du
4

D.

0

0

π
2

∫u

3

1 − u 2 du

0

3

94) Đổi biến u = tan

A.

1
3

dx
x
thì tích phân I = ∫
thành:
cos x
2
0

2du

∫ 1− u

B.

2

0

1
3

du

∫ 1− u

C.

2

0

1
3

2udu

∫ 1− u

D.

2

0

1

3

udu

∫ 1− u

2

0

*ỨNG DỤNG TÍCH PHÂN TÍNH DIỆN TÍCH – THỂ TÍCH
95) Diện tích hình phẳng giới hạn bởi Parabol
A.

125
6

B.

và đường thẳng

65
6

C.

95
6

bằng:

D. −

125
6

96) Công thức nào sau đây là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên [a;b], và các đường
y = 0, x = a, x = b
b

A. S =

∫

B. S = π

f ( x) dx

a

b

∫

b

C. S =

f ( x) dx

a

∫ [ f ( x) ]

2

D. S = π

dx

a

b

∫ [ f ( x) ]

2

dx

a

97) Diện tích hình phẳng giới hạn bởi các đường y = x 2 , trục Ox, và đường thẳng x = 2 là

16
8
D.
3
3
98) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x 2 − 4 x + 5 và hai tiếp tuyến với đồ thị hàm số tại A(1;2) và
A.

8
3

C. −

B. 16

a
. Khi đó a + b bằng
b
9
B. 12
C.
4

B(4;5) có kết quả dạng
A.13

D.

13
12

99) Thể tích của khối tròn xoay do hình (H) giới hạn bởi các đường y = x 3 + 1; y = 0; x = 0 và x = 1 quay quanh trục
hoành là
A. V = π

1

∫(x
0

3

)

2

+ 1 dx

B. V = π

1

∫(x
0

3

)

+ 1 dx

1

C. V =

∫(x

3

)

2

+ 1 dx

0

1

D. V =

∫x
0

100) Thể tích khối tròn xoay khi quay quanh trục Ox hình phẳng giới hạn bởi các đường

y = x ln x, y = 0, x = e có giá trị bằng:

π
(b e3 − 2) trong đó a,b là hai số thực nào dưới đây?
a

3

+ 1dx

Trần Thị Thanh Tuyền (tổng hợp và biên soạn)
A.a=27; b=5

Phan Huy Chú- Khánh Xuân - BMT

B.a=24; b=6

C.a=27; b=6

D.a=24; b=5

101) Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y =
quanh trục ox là:
A. 8π

B. 4π

C. 12π

D. 6π

 y = s inx
 y=0

102) Tính diện tích hình phẳng giới hạn bởi các đường 
 x=0
 x=2π
A.4

B. 0

4
, y = 0 , x =1, x = 4
x

C.2

D. 1

103) Cho hình phẳng giới hạn bởi dường cong y = tan x , trục hoành và hai đường thẳng x = 0, x =

π
. Tính thể tích
4

V khối tròn xoay thu được khi quay hình phẳng này xung quanh trục Ox .




A. V = −π 1 −

π
÷
4




B. V = 1 −

π
÷
4




C. V = π 1 −

π
÷
4




D. V = π  2 −

π
÷
4

104) Tính diện tích hình phẳng giới hạn bởi y = x x 2 + 1 ; x = 1 và trục Ox.
A.

2 2 −1
3

B.

3 2 −1
5

C.

5−2 2
3

D.

5− 2
6

105) Tính diện tích hình phẳng giới hạn bởi y = x² và y = 2x
A.

4
3

B.

8
3

C.

7
3

D. 3

106) Tính diện tích hình phẳng giới hạn bởi ( P ) : y = x 2 + 1 ; trục Oy và tiếp tuyến với (P) tại điểm M(2; 5)
A.

7
3

B.

5
3

107) Cho hình (H) giới hạn bởi y =
quanh trục Ox.
A. π

B. πe

108) Cho hình (H) giới hạn bởi y =

C. 2

D.

8
3

xe x ; x = 0; x = 1; trục Ox. Tính thể tích khối tròn xoay khi quay hình (H)
C. π(e – 1)

D. π(e + 1)

2
; x = 1; x = 2; y = 0 . Tính thể tích vật thể tròn xoay khi quay hình (H) quanh
x

trục Ox.
A. 4π
B. 2π
C. 5π
D. 3π
109) Cho hình (H) giới hạn bởi y = sin x; x = 0; x = π và y = 0. Tính thể tích vật thể tròn xoay khi quay hình (H)
quanh trục Ox.
A. V = 2π
B. V = π²/2
C. V = π²/4
D. V = π/2
110) Cho hình (H) giới hạn bởi các đường y = x và y = x. Tính thể tích vật thể tròn xoay khi quay hình (H) quanh
trục Ox.
A. π
B. π/6
C. π/3
D. π/2
111) Tính diện tích hình phẳng giới hạn bởi y = –2x² + x + 3 và trục hoành là
A. 125/24
B. 135/24
C. 125/12
D. 65/12
112) Tính diện tích hình phẳng giới hạn bởi y = –x³ + 3x + 1 và đường thẳng y = 3 là

A. 57/4.
B. 45/4 .
C. 27/4.
D. 21/4.
113) (Đề thử nghiệm lần 2 BGD)Cho hình thang cong ( H ) giới hạn bới các
đường y = e x , y = 0, x = 0 và x = ln 4 . Đường thẳng

x = k (0 < k < ln 4) chia ( H ) thành hai phần có diện


Trần Thị Thanh Tuyền (tổng hợp và biên soạn)

Phan Huy Chú- Khánh Xuân - BMT

tích là S1 S 2 và như hình vẽ bên. Tìm x = k để S1 = 2 S 2 .

2
ln 4
3
8
C. k = ln
3
A. k =

B. k = ln 2
D. k = ln 3

114) (Đề thử nghiệm lần 2 BGD)Ông An có một mảnh vườn hình elip có độ dài trục
lớn bằng 16m và độ dài trục bé bằng 10m. Ông muốn trồng
hoa trên một dải đất rộng 8m và nhận trục bé của elip làm trục

đối xứng( như hình vẽ). Biết kinh phí để trồng hoa 100.000
đồng/1 m2. Hỏi Ông An cần bao nhiêu tiền để trồng hoa trên
dải đất đó? ( Số tiền được làm tròn đến hàng nghìn)
A. 7.862.000 đồng
B. 7.653.000 đồng
C. 7.128.000 đồng
D. 7.826.000 đồng
115) Cho hình phẳng D giới hạn bởi: y = tan x; x = 0; x =

π
; y = 0 gọi S là diện tích hình phẳng giới
3

hạn bởi D. gọi V là thể tích vật tròn xoay khi D quay quanh ox. Chọn mệnh đề đúng.



A. S = ln 2, V = π  3 +





C. S = ln 3, V = π  3 +




π
π

÷ B. S = ln 2, V = π  3 − ÷
3
3


π
π
÷D. S = ln 3, V = π  3 − ÷
3
3


116) Thể tích khối tròn xoay tạo thành khi cho đường x2+(y-1)2=1 quay quanh trục hoành là
A. 8π 2
B. 4π 2
C. 2π 2
D. 6π 2