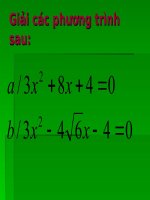Công thức nghiệm
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (652.4 KB, 17 trang )
Thứ 7, ngày 10 tháng 03 năm 2007.
Tiết 53
CÔNG THỨC NGHIỆM CỦA
PHƯƠNG TRÌNH BẬC HAI
(Đại số 9)
Kiểm tra bài cũ:
2. Giải phương trình sau bằng cách biến đổi phương trình
thành phương trình có vế trái là bình phương của 1 biểu
thức, còn vế phải là một hằng số.
3x
2
+ 7x + 1 = 0
1. Phát biểu định nghĩa phương trình bậc hai một ẩn ?
Tiết 53: Công thức nghiệm của phương trình bậc
hai
31
x
2
+
x37
=
x
2
+
2.
x.
3.27
=
x
2
+
2.
x.
+
=
+
3x
2
+ 7x =- 1
3x
2
+ 7x+1=0
+
=
1. Công thức nghiệm:
ax
2
+ bx + c = 0 (a 0) (1)
ax
2
+ bx = - c
x
2
+
a
c
x
a
b
=
a
c
a
b
xx
=+
.2
..2
2
a
c
a
b
a
b
x =
+
2
2
2
42
2
2
2
4
4
2 a
acb
a
b
x
=
+
(2)
2
2
+
a
b
a
b
xx
2
.2
2
+
a
c
=
2
2
+
a
b
3
1
x
2
+
x
3
7
=
x
2
+ 2.x.
3
1
3.2
7
=
3x
2
+ 7x = - 1
2
7 1 49 37
6 3 36 36
x
+ = + =
ữ
Em hãy biến đổi phương trình tổng
quát về dạng có vế trái là bình phư
ơng của một biểu thức, vế phải là
hằng số ?
2
6
7
2
6
7
x
2
+ 2.x.
6
7
3
1
+
=
+
Dựa vào các bước biến đổi đã có
của phương trình
Thứ 5 ngày 27 tháng 3 năm 2008
1. Công thức nghiệm:
ax
2
+bx +c = 0 (a 0) (1)
ax
2
+bx = - c
x
2
+
a
c
x
a
b
=
a
c
a
b
xx
=+
.2
..2
2
a
c
a
b
a
b
x =
+
2
2
2
42
2
2
2
4
4
2 a
acb
a
b
x
=
+
(*)
Người ta kí hiệu
=b
2
-4ac
2
2
+
a
b
a
b
xx
2
.2
2
+
a
c
=
2
2
+
a
b
Như vậy, chúng ta đã biến
đổi phương trình (1) thành
phương trình (*) có vế trái là
bình phương của một biểu
thức, còn vế phải là một
hằng số.
Ta có thể khai phương hai
vế để tìm được x chưa ?
Tiết 53: Công thức nghiệm của phương trình bậc hai
Thứ 5 ngày 27 tháng 3 năm 2008
Ta có:
2
2
42 aa
b
x
=
+
(2)
?1
?1
Hãy điền những biểu thức thích hợp vào các chỗ trống (...) dưới đây:
a) Nếu >0 thì từ phương trình (2) suy ra
...
2
=+
a
b
x
Do đó, phương trình (1) có hai nghiệm: x
1
= ..., x
2
= ...
b) Nếu = 0 thì từ phương trình (2) suy ra
...
2
=+
a
b
x
Do đó, phương trình (1) có nghiệm kép x = ...
?2
?2
Hãy giải thích vì sao khi < 0 thì phương trình vô nghiệm.
Do ®ã, ph¬ng tr×nh (1) cã hai nghiÖm:
±=+
a
b
x
2
a) NÕu ∆ > 0 th× tõ ph¬ng tr×nh (2) suy ra
?1
?1
?2
?2
NÕu ∆ < 0 th× ph¬ng tr×nh (1) v« nghiÖm
(v× ph¬ng tr×nh (2) v« nghiÖm do vÕ ph¶i lµ mét sè ©m cßn
vÕ tr¸i lµ mét sè kh«ng ©m )
a2
∆
b) NÕu ∆ = 0 th× tõ ph¬ng tr×nh (2) suy ra
0
2
=+
a
b
x
Gi¶i:
2
2
42 aa
b
x
∆
=
+
(2)
,
a
b
2
∆+−
x
1
=
a
b
2
∆−−
x
2
=
Do ®ã, ph¬ng tr×nh (1) cã nghiÖm kÐp
a
b
2
−
x =