Tiiệm cậnị( T12 cua Vân - THĐ - HP)
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (379.65 KB, 16 trang )
O
x
y
O
x
y
O
x
y
O
x
y
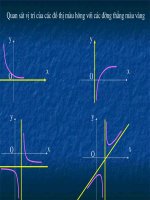
Quan s¸t vÞ trÝ cña c¸c ®å thÞ mµu h«ng víi c¸c ®êng th¼ng mµu vµng
Tiệm cận
Tiệm cận
1.Đinh nghĩa:giả sử hàm số y = f(x) có đồ thị là (C) và M(x;y)
1.Đinh nghĩa:giả sử hàm số y = f(x) có đồ thị là (C) và M(x;y)
là một điểm thay đổi trên (C).
là một điểm thay đổi trên (C).
a)Nhánh vô cực của đồ thị hàm số là gì?
a)Nhánh vô cực của đồ thị hàm số là gì?
Ta nói (C) có nhánh vô cực nếu ít nhất một trong hai tọa độ x, y
Ta nói (C) có nhánh vô cực nếu ít nhất một trong hai tọa độ x, y
dần tới
dần tới
và viết M
và viết M
x
x
hoặc y
hoặc y
O
x
y
d
M
H
M
H
M
H
M
H
M
H
M
H
Cho đường thẳng d
và MH = d(M,d)
D là tiệm cận của (C)
Lim MH = 0
M0
M(C)
b)Tiệm cận của đồ thị hàm số là gì?
O
x
y
O
x
y
O
x
y
O
x
y
Quan s¸t vÞ trÝ cña c¸c ®å thÞ mµu hång víi c¸c ®êng th¼ng mµu vµng
TiÕt:TiÖm cËn
ThiÕt kÕ vµ thùc hiÖn:NguyÔn ThÞ V©n
Gi¸o viªn:THPT TrÇn Hng §¹o
2.Các loại tiệm cận
Giả sử d là một tiệm cận của đồ thị hàm số y = f (x)
a)Nếu d cùng phương với Oy ta gọi d là tiệm cận đứng..
b) Nếu d cùng phương với Ox ta gọi d là tiệm cận ngang.
c) Nếu d không thuộc hai loại trên ta gọi d là tiệm cận xiên.
3.Dấu hiệu tiệm cận của đồ thị y = f (x).
Định lý:Nếu lim f(x) =
xx
0
Thì d : x = x
0
là tiệm cận đứng của (C).
a) Tiệm cận đứng
Chứng minh
Định lý: Nếu lim f(x) =
xx
0
Thì d : x = x
0
là tiệm cận đứng của (C).
O
x
y
x
0
M
x
y
H
lim f(x) = khi xx
0
thì y = f(x)
xx
0
=> M(x;y) => đồ thị có nhánh vô cực
Khi đó MH = |x-x
0
|0 (khi M(x;y) )
lim MH = 0 d có phương trình x = x
0
là một tiệm cận đứng của (C)
M
Chứng minh
3.Dấu hiệu tiệm cận của đồ thị y = f (x).(tiếp)