A

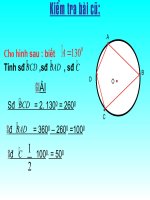
Kiểm tra bài cũ
* Kiến thức cần nhớ
Một tam giác được gọi là nội tiếp đường tròn
(hay đường tròn ngoại tiếp tam giác) khi cả
ba đỉnh của tam giác nằm trên đường tròn
đó.
Tâm của đường tròn ngoại tiếp tam giác là
giao điểm ba đường trung trực của tam giác
đó. có duy nhất một đường tròn đi qua ba điểm không thẳng hàng
Chỉ
Trong một đường tròn,
+) Số đo của góc nội tiếp bằng nửa số đo cung bị
chắn.
+) Các góc nội tiếp bằng nhau chắn các cung bằng
nhau.
+) Các góc nội tiếp cùng chắn một cung hoặc chắn
các cung bằng nhau thì bằng nhau

C=E=D=

1
sđ AmB (cỏc gúc nột tiếp cựng chắn AmB)
2

O
B

C

A

.
O
B
C

C

A

m
E

O
B
D


A

a) Vẽ đường tròn tâm (O), rồi vẽ tứ giác ABCD
có tất cả các đỉnh nằm trên đường tròn đó.

B
D

O

C


b) Vẽ một đường tròn tâm (I), rồi vẽ tứ giác MNPQ có
3 đỉnh nằm trên đường tròn đó còn đỉnh thứ tư thì không
M

M

I

Q

P

N

I

Q

N

P

Minh hoạ


TIẾT
48:

HÌNH HỌC 9


1. Khái niệm tứ giác nội tiếp.
Định nghĩa: SGK

Bài tập: Hãy chỉ ra các tứ giác nội tiếp
trong hình sau:
A

Một tứ giác có bốn đỉnh nằm trên đường
tròn được gọi là tứ giác nội tiếp đường tròn
A
(gọi tắt là tứ giác nội tiếp)
Ví dụ: Tứ giác ABCD có
4 đỉnh: A, B, C, D ∈ O,
⇒ tứ giác ABCD nội tiếp
đường tròn (O).

D

P

M

O
C
C
M

O


N

O

B

M

Q

B

E

O

Q

P

Tứ giác MNPQ không nội tiếp

N

D

Các tứ giác nội tiếp đường tròn (O):
ABCD, ABDE, ACDE
Tứ giác AMDE có
không

nội tiếp
nội tiếp đường tròn (O).
đường tròn (O) không?
Tứ giác AMDE không
có thể nội
thể nội
tiếptiếp bất kỳ
đường
một đường
tròn tròn
nào vỡ
nàogiả
đósử
không?
tứ giácVỡ
AMDE
sao?
nội tiếp một đường tròn (O’) thỡ khi đó, qua
3 điểm: A, E, D tồn tại 2 đường tròn (O) và
(O’) khác nhau. Điều này là vô lí.


TIẾT
48: A

HÌNH HỌC 9

1. Khái niệm tứ giác nội tiếp.
Định nghĩa: SGK


A, B, C, D

∈(O)

Chứng minh
B

D

1
sđ BCD (góc nội tiếp chắn BCD)
2
1
C = sđ BAD (góc nội tiếp chắn BAD)
2

O

⇒ ABCD là tứ giác nội tiếp.
2. Định lí:

Ta có: A =
C

Trong một tứ giác nội tiếp, tổng số đo hai góc
đối diện bằng 1800.

⇒

GT Tứ giác ABCD nội tiếp (O)

KL A + C = 1800

;

B + D = 1800
A

B

1
sđ ( BCD + BAD)
2
1
= .3600 =1800
2

A+C =

Chứng minh tương tự ta cũng có:
B + D = 1800

O
D
C

Minh hoạ


HÌNH HỌC 9


TIẾT
48:

1. Khái niệm tứ giác nội tiếp.
Bài tập:
2. Định lí:
Biết ABCD là tứ giác nội tiếp. Hãy điền
Trong một tứ giác nội tiếp, tổng số đo hai góc vào ô trống trong bảng sau (nếu có thể)
A
đối diện bằng 1800.
ABCD là tứ giác nội tiếp.
0

A+ C = 180 0 ; B + D =
180

B

D
O

A
C

B

O
D
C


T.H
Góc

1)

2)

3)

A

900

880

800

B

600

1100

C

900

920

D


1200

700

4)

500
1000
1300

5)

6)

1040

850

750

720

760

950

1050

1080



HÌNH HỌC 9

TIẾT
48:

1. Khái niệm tứ giác nội tiếp.
2. Định lí:
Trong một tứ giác nội tiếp, tổng số đo hai
góc đối diện bằng 1800
3. Định lí đảo:
Nếu một tứ giác có tổng số đo hai góc
đối diện bằng 1800 thì tứ giác đó nội
tiếp được đường tròn

Hình

B
B = 70°
D = 110°
B+D = 180°

A
D

C


TIẾT

48:

HÌNH HỌC 9

1. Khái niệm tứ giác nội tiếp.
Bài Tập: Trong các hình vẽ sau, hình
2. Định lí:
nào không nội tiếp đường tròn?
Trong một tứ giác nội tiếp, tổng số đo hai
góc đối diện bằng 1800
3. Định lí đảo:
Nếu một tứ giác có tổng số đo hai góc
đối diện bằng 1800 thì tứ giác đó nội
tiếp được đường tròn

A. Hình chữ nhật

B. Hình bình hành

A

O

m

B

D
C


C. Hình vuông

Hình

D. Hình thang cân


HÌNH HỌC 9

TIẾT
48:

1. Khái niệm tứ giác nội tiếp.
2. Định lí:

Trong một tứ giác nội tiếp, tổng số đo hai
góc đối diện bằng 1800

B

A

B
A
115 °

O

D


D

65°

C

C

3. Định lí đảo:
Nếu một tứ giác có tổng số đo hai góc

A

đối diện bằng 1800 thì tứ giác đó nội
tiếp được đường tròn

A
B

90°

x

B

*Dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có bốn đỉnh cách đều một điểm

90 °


D

D

C

- Tứ giác có tổng hai góc đối diện bằng 1800
- Tứ giác có góc ngoài tại một đỉnh bằng góc
trong của đỉnh đối diện

C

B
B

A

A

- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh
chứa hai đỉnh còn lại dưới 2 góc bằng nhau.

D

O

D

C


O

C


TIẾT
48:

HÌNH HỌC 9

Luyện tập:
1. Khái niệm tứ giác nội tiếp.
Bài 1: Cho tam giác nhọn ABC, vẽ
2. Định lí:
các đường cao AH, BK, CF. Hãy tìm
Trong một tứ giác nội tiếp, tổng số đo hai các tứ giác nội tiếp trong hình vẽ.
góc đối diện bằng 1800
A
3. Định lí đảo:

Nếu một tứ giác có tổng số đo hai góc

K

đối diện bằng 180 thì tứ giác đó nội
tiếp được đường tròn
0

*Dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có bốn đỉnh cách đều một điểm

- Tứ giác có tổng hai góc đối diện bằng 1800
- Tứ giác có góc ngoài tại một đỉnh bằng góc
trong của đỉnh đối diện
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh
chứa hai đỉnh còn lại dưới 2 góc bằng nhau.

F

.O

B

C
H
-Các tứ giác: AFOK, BFOH, CHOK nội
tiếp, vì có tổng số đo hai góc đối bằng
1800.
-Tứ giác BFKC có BFC = BKC = 900
⇒ Tứ giác BFKC nội tiếp.
-Tương tự: các tứ giác AFHC; AKHB
nội tiếp.
Kiem chung


HÌNH HỌC 9

TIẾT
48:

1. Khái niệm tứ giác nội tiếp.

2. Định lí:
Trong một tứ giác nội tiếp, tổng số đo hai
góc đối diện bằng 1800
3. Định lí đảo:

Bài 2(Bài 54-SGK/89)
Cho Tứ giác ABCD có
ABC+ADC=1800
Chứng minh
rằng các đường trung trực của AC, BD,
AB cùng đi qua một điểm A
Bài làm

Nếu một tứ giác có tổng số đo hai góc

đối diện bằng 1800 thì tứ giác đó nội
tiếp được đường tròn

*Dấu hiệu nhận biết tứ giác nội tiếp:
- Tứ giác có bốn đỉnh cách đều một điểm
- Tứ giác có tổng hai góc đối diện bằng 1800
- Tứ giác có góc ngoài tại một đỉnh bằng góc
trong của đỉnh đối diện
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh
chứa hai đỉnh còn lại dưới 2 góc bằng nhau.

-Vì ABC+ADC=1800
Nên tứ giác ABCD nội tiếp
được một đường tròn, gọi
tâm đường tròn đó là (O)


.

O

B

D
C

-Ta có OA=OC nên điểm O thuộc trung trực AC (1)
OB=OD nên điểm O thuộc trung trực BD (2)
OA=OB nên điểm O thuộc trung trực AB (3)
Từ (1)(2)(3) suy ra ba đường trung trực của AC, BD,
AB cùng đi qua điểm O


HƯỚNG DẪN VỀ NHÀ
- Nắm định nghĩa, định lí về tứ giác nội tiếp.
- Vận dụng các dấu hiệu nhận biết tứ giác nội tiếp để giải
bài tập.
- Bài tập về nhà: 55, 56, 57, 58 trang 89 – SGK.


Bài tập 56: Tính các góc của tứ giác ABCD trong hình vẽ.

E
B

40 °


C

O
A

D

20 °

F


E

BÀI 56 (SGK)

40°

Tính số đo các góc của tứ giác ABCD ?
GỢI Ý
ĐÆt x = BCE = DCF (®èi dØnh)

B
C
O

A

20°


D

ABC = 400 + x (góc ngoài ∆BEC)
(1)
ADC = 200 + x (góc0 ngoài ∆CDF)
(2)
ABC + ADC = 180 ( vỡ tứ giác ABCD nội tiếp (O) )
Từ (1) , (2) và (3) suy ra 1800 = 600 + 2x ⇒ x = 600
Từ (1) suy ra ABC = 1000
0
Từ (2) suy ra
0 ADC = 80
0
BCD = 180 – x = 120 ( 2 góc kề bù)

BAD = 1800 – BCD = 600 (2 góc đối của tứ giác ABCD)

F

(3)


Bài tập 56: Tính các góc của tứ giác ABCD trong hình vẽ.
Trong ∆EADcó: A + D2 = 1800 − E = 1800 − 400 = 1400
Trong ∆FAB có: A + B2 = 1800 − F = 1800 − 200 = 1600
A + D2 = 1400 
0
0
0

⇒
2
A
+
D
+
B
=
140
+
160
=
300

2
2
A + B2 = 1600 

E

Tứ giác ABCD nột tiếp nên ta có: B2 + D2 = 1800

B
2

1

40 °

⇒ 2 A = 1200 ⇒ A = 600 ⇒ C = 1200


C

A = 600 ⇒ B2 = 1000
A = 600 ⇒ D2 = 800

O
A

2

1

D

20 °

F