BI GIảNG MÔN HọC TíN HIệU V Hệ THốNG
Nguyễn Doãn Phớc
Bộ môn ĐKTĐ, Trờng ĐHBK H Nội

Mục lục
1
1.1
1.2

Khái niệm tín hiệu v hệ thống
1
Định nghĩa tín hiệu và phân loại tín hiệu ........................................................................................... 1
Định nghĩa hệ thống và phân loại hệ thống ...................................................................................... 3

2
2.1
2.2
2.3

Biểu diễn trên miền thời gian
5
Đáp ứng thời gian và mô hình đáp ứng xung .................................................................................... 5
Mô hình trạng thái hệ liên tục............................................................................................................ 8
Mô hình trạng thái hệ không liên tục ................................................................................................. 9

3
3.1
3.2

Chuỗi Fourier v phép biến đổi Fourier
10

Chuỗi Fourier .................................................................................................................................. 10
Phép biến đổi Fourier (toán tử Fourier)........................................................................................... 12

4
4.1
4.2
4.3

Đáp ứng tần số v lọc tín hiệu
16
Đặc tính tần số và đồ thị hàm đặc tính tần...................................................................................... 16
Đáp ứng tần số và quan hệ với đáp ứng thời gian .......................................................................... 17
Lọc tín hiệu...................................................................................................................................... 19

5
5.1
5.2

Phép biến đổi Laplace v hm truyền hệ liên tục
21
Phép biến đổi Laplace (toán tử Laplace) ........................................................................................ 21
Hàm truyền mô tả hệ liên tục tuyến tính tham số hằng................................................................... 23

6
6.1
6.2

Phép biến đổi Z v hm truyền hệ không liên tục
24
Phép biến đổi Z............................................................................................................................... 24

Hàm truyền mô tả hệ tuyến tính không liên tục............................................................................... 26

Một số điều lu ý

27

Ti liệu tham khảo
[1]

Carlson,G.E.: Signal and linear Systems Analysis with MatLab (in lần thứ 2). John Wiley & Sons

[2]
[3]

Sundararajan,D.: A Practical Approach to Signal and Systems. John Wiley & Sons Inc., 2008.
Phớc,N.D.&Minh,P.X.: Nhận dạng các hệ thống điều khiển (in lần thứ 3). NXB Khoa học và Kỹ

[4]

thuật, 2005.
Tú Anh,Đ.: Slides bài giảng môn học Tín hiệu và Hệ thống, Trờng ĐHBK Hà Nội, 2008.

Inc., 1998.

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

29


1


Khái niệm tín hiệu và hệ thống

1.1

Định nghĩa tín hiệu v phân loại tín hiệu

Định nghĩa: Tín hiệu l một hoặc nhiều hm thời gian, mang thông tin vật lý v đợc
truyền tải bằng một đại lợng vật lý (khác).
Ví dụ: Tiếng nói l một đại lợng vật lý. Tiếng nói đợc biến đổi thnh dòng điện l
một đại lợng vật lý khác để truyền hữu tuyến đi xa. Dòng điện đợc mô tả bằng một
hm thời gian i(t). Nh vậy hm thời gian i(t) ở đây l một tín hiệu, nó mang thông
tin của tiếng nói v đợc truyền tải nhờ dòng điện.
Phân loại: Cơ sở để phân loại tín hiệu l hm thời gian x(t) mô tả nó. Chúng đợc
phân loại thnh từng cặp (phạm trù) riêng biệt:
1)

liên tục v không liên tục (phân loại thông qua miền xác định t R ). Một tín hiệu
đợc gọi l liên tục, nếu hm x(t) mô tả nó liên tục từng đoạn, ngợc lại nó đợc
gọi l tín hiệu không liên tục. Tín hiệu không liên tục đợc mô tả bằng dãy các giá
trị {x k }, k=,1,0,1,, trong đó x k l giá trị (trích mẫu) của x(t) tại điểm thời
gian t=kT a , tức l x k =x(kT a ).

2)

tơng tự v rời rạc (phân loại thông qua miền giá trị x R ). Tín hiệu tơng tự l
tín hiệu m hm x(t) mô tả nó có miền giá trị tạo thnh từng khoảng liên thông,
ngợc lại nó sẽ đợc gọi l tín hiệu rời rạc. Chẳng hạn tín hiệu có giá trị chỉ l
những số hữu tỷ l tín hiệu rời rạc.


3)

tiền định v ngẫu nhiên (phân loại theo sự mô tả bởi một hay nhiều hm),

4)

tuần hon v không tuần hon,

5)

nhân quả v phi nhân quả (causal v uncausal). Tín hiệu nhân quả l hm x(t)
thỏa mãn x(t)=0 khi t<0, ngợc lại nó sẽ đợc gọi l phi nhân quả.

Việc phân chia chúng thnh từng cặp nh vậy để nói rằng một tín hiệu không thể có
các tính chất trong cùng một cặp. Chẳng hạn không thể có tín hiệu vừa tơng tự, vừa
rời rạc, song lại có tín hiệu vừa không liên tục v vừa rời rạc. Tín hiệu không liên tục
v rời rạc đợc gọi l tín hiệu số.
Ngoi ra, tín hiệu còn đợc đánh giá qua P =









2

x( t ) dt , E = x( t ) dt , gọi l công


suất v năng lợng, tức l chuẩn bậc 1 v bậc 2 của hm.
Một số tín hiệu điển hình: Tín hiệu điển hình đợc hiểu l những tín hiệu cơ bản nhất
m các tín hiệu khác biểu diễn đợc thông qua chúng.
1)

1 khi t 0
Tín hiệu bớc nhảy đơn vị (hm Heaviside): 1( t ) =
0 khi t < 0

2)

1 khi T t < T
Tín hiệu xung vuông (hm cửa sổ): w( t ) = 1( t + T ) 1( t T ) =
0 khi t [ T , T )

3)

Tín hiệu tăng đều: r( t ) = t 1( t )

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

1


4)

Tín hiệu điều hòa: x1 ( t ) = sin( t + ) v x2 ( t ) = cos( t + )

5)


Xung dirac: ( t ) =

d1( t )
. Vì hm 1(t) không liên tục tại 0, tức l tại đó không tồn
dt
tại đạo hm, nên định nghĩa trên không chặt chẽ. Nó đợc thay bằng:
x( t ) =



x( ) ( t )d x( t )

(t)

x(0) =





x( t ) ( t )dt với x(t) (t)=x(0) (t)

(1.1)



tức l xung dirac đợc xem nh một ánh xạ : x(t)

x(0) R từ không gian hm


số vo trờng số thực. Dấu tích phân trong (1.1) không có ý nghĩa về mặt toán
học, nó chỉ có nghĩa rằng phép tính đó có tính chất giống nh một tích phân v
ngời ta gọi nó l hm mở rộng (t). Công thức (1.1) đợc suy ra từ việc xấp xỉ
hm liên tục x(t) bất kỳ thnh tổng tuyến tính của các hm xung vuông:
x( t )





xk 1( t kTa ) 1( t ( k + 1)Ta = x( kTa ) 1( t kTa ) 1( t ( k + 1)Ta

k =

k =


1( t kTa ) 1( t ( k + 1)Ta
d1( t )
Ta = x( )
d
x( t ) = lim x( kTa )
Ta 0 k =
Ta
dt



=




đ.n.

x( ) ( t )d = x( t ) * ( t )



Ký hiệu * l chỉ phép tích chập. Phép tích chập l giao hoán đợc.
6)

Hm trích mẫu (hình 1.1): s( t ) =



( t kTa )

(1.2)

k =

Vì xung dirac l hm mở rộng nên s(t) cũng l một hm mở rộng. Từ hm trích
mẫu ny thì tín hiệu không liên tục {x k }, k=,1,0,1,, thu đợc từ việc trích
mẫu xk=x(kTa) của tín hiệu liên tục x(t), với Ta l chu kỳ trích mẫu sẽ có dạng:
đ.n.

{x k }=x(t)s(t) = x( t )
Nh vậy tín hiệu không liên tục x( t ) ={x k } cũng l một hm mở rộng.
Bi tập:

Cho hai tín hiệu

x1 ( t ) = t a 1( t ) 1( t b) v x2 ( t ) = t c1( t d ) , trong đó 0
1
2
hạn nhng lại có E hữu hạn.

0
Hình1.1: Đồ thị hàm trích mẫu

2

Hình1.2: Cấu trúc hệ thống

Hình1.3: Hệ thống bình trộn

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


1.2

Định nghĩa hệ thống v phân loại hệ thống

Định nghĩa: Hệ thống l tập hợp các phần tử (linh kiện, thiết bị, phơng pháp, thuật
toán ) đợc kết nối với nhau để thực hiện một nhiệm vụ cụ thể v có giao tiếp với
môi trờng bên ngoi bằng các tín hiệu vo v ra (hình 1.2).
Ví dụ: Hệ thống bình trộn dung dịch (hình 1.3). Các phần tử của chúng gồm hai bình

chứa dung dịch khác nhau, các đờng ống dẫn dung dịch v hai van chỉnh lu lợng
đợc kết nối với nhau cả về mặt cơ khí v cả về các định luật cân bằng. Hệ thống bình
trộn giao tiếp với môi trờng bên ngoi bằng các độ mở van (tín hiệu vo) v nồng độ
dung dịch chảy ra (tín hiệu ra).
Phân loại: Cơ sở để phân loại hệ thống gồm 4 yếu tố: số các tín hiệu vora, cấu trúc
liên kết các phần tử bên trong, nhiệm vụ của hệ thống v dạng tín hiệu giao tiếp với
môi trờng xung quanh:
1)

Số tín hiệu vora: Hệ SISO, nếu hệ chỉ có một tín hiệu vo v một tín hiệu ra.
Tơng tự l các hệ MIMO, MISO, SIMO.

2)

Cấu trúc liên kết các phần tử: Hệ kín l hệ có ít nhất một đờng mô tả mối liên
kết giữa các phần tử tạo thnh vòng kín, ngợc lại đợc gọi l hệ hở.

3)

Nhiệm vụ của hệ thống: Nếu ký hiệu các tín hiệu vo l u = (u1 , , um )T , các tín
hiệu ra l y = ( y1 , , y p )T thì nhiệm vụ của hệ sẽ chính l ánh xạ (mô hình):

T :u
a)

y hay y = T ( u)

(1.3)

Hệ tham số hằng, nếu mô hình toán T : u

y của nó không thay đổi (theo

thời gian v theo không gian. Ngợc lại hệ sẽ đợc gọi l không dừng, nếu mô
hình của nó thay đổi theo thời gian (thờng còn đợc gọi l hệ nonautonom),
hoặc hệ phân bố rải, nếu mô hình của nó thay đổi theo không gian.
b)

Hệ tuyến tính, nếu ánh xạ T l tuyến tính, ngợc lại thì đợc gọi l phi tuyến.

c)

Hệ nhân quả (causal), nếu mô hình toán y = T ( u) của nó thỏa mãn:
y( t ) = T ( u( )) khi 0 t (chỉ phụ thuộc hiện tại v quá khứ của u )
ngợc lại thì đợc gọi l phi nhân quả (phụ thuộc cả thời tơng lai của u ) .

d) Hệ tĩnh, nếu có y( t ) = T ( u( )) khi t= , ngợc lại thì gọi l động.
4)

Tín hiệu giao tiếp bên ngoi: Hệ liên tục, nếu tín hiệu vora l liên tục u( t ), y( t ) ,
ngợc lại nếu tín hiệu vora l không liên tục {uk },{ y } , thì đợc gọi l hệ không
k

liên tục. Hệ có tín hiệu vora vừa không liên tục, vừa rời rạc đợc gọi l hệ số.
Mô tả hệ thống: L hình thức biểu diễn ánh xạ T trong (1.3). Công việc xác định ánh
xạ T đợc gọi l mô hình hóa. Các hình thức mô tả cơ bản bao gồm:
1)

Mô hình vora (phơng trình vi phân) cho hệ liên tục:

(

)

f y, y(1) , , y( n ) , u, u(1) , , u( m ) = 0

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

(1.4)

3


2)

Mô hình vora (phơng trình sai phân) cho hệ không liên tục:

(

f y ,y
3)

k

k 1

, ,y

k n

)

, uk , uk 1 , , u k m = 0

(1.5)

Mô hình trạng thái (hệ phơng trình vi phân) cho hệ liên tục:
dx
= f ( x, u) v y = g( x, u )
dt

(1.6)

trong đó x = ( x1 , , xn )T l vector các đại lợng trạng thái (bên trong) hệ.
4)

Mô hình trạng thái (hệ phơng trình sai phân) cho hệ không liên tục:
x k +1 = f ( x k , uk ) v yk = g( x k , uk )

(1.7)

Sơ đồ khối: Biểu diễn cấu trúc bên trong một hệ lớn gồm nhiều hệ con hợp thnh,
cùng các đờng nối liên kết tín hiệu vora giữa các hệ con đó (hệ con còn đợc gọi l
khâu hoặc khối). Ngoi ra trong sơ đồ khối còn có các nút cộng, trừ hoặc các nút tách
(chia) tín hiệu. ánh xạ vora Tk của từng khối đợc biểu diễn kèm theo bằng cách
viết vo bên trong khối đó (hình 1.4). Sơ đồ khối có ba cấu trúc cơ bản, đó l:
1)
2)
3)

Hai khối mắc nối tiếp.
Hai khối mắc song song.
Hai khối mắc hồi tiếp.

Bi tập:
1)

2)

Hãy xây dựng mô hình vora cho các hệ
SISO ở hình 1.5, trong đó u(t) l tín hiệu
vo v y(t) l tín hiệu ra của hệ.

Xây dựng mô hình trạng thái tơng đơng cho hệ có mô hình vora:
y( n ) + a1 y( n 1) +

3)

+ an y = b0u

Hãy chỉ rằng hệ liên tục với mô hình trạng thái
y( n ) + a1 y( n 1) +

4)

Hình 1.4: Sơ đồ khối của một hệ thống

+ an y = b0u( m ) + b1u( m 1) +

a)

l hệ tuyến tính,

b)

l hệ phi nhân quả nếu có m>n.

+ bmu

Viết công thức lặp xác định tín hiệu ra y theo tín hiệu vo uk cho hệ không liên
k

tục với mô hình trạng thái
x k +1 = Ax k + Buk v yk = Cx k + Duk , x0 tùy ý cho trớc.

Hình 1.5: Cho bài tập 1. Các hệ thống điện, thủy khí và cơ khí.

4

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


2

Biểu diễn trên miền thời gian

2.1

Đáp ứng thời gian v mô hình đáp ứng xung

Hệ không liên tục: Mô hình vora (1.5) của hệ tuyến tính SISO không liên tục, tham
số hằng, có dạng:
yk + a1 yk 1 +

+ an yk n = b0uk + b1uk 1 +

+ bmuk m

(2.1)

Bi toán xác định đáp ứng của hệ (2.1) đợc hiểu l xác định dãy giá trị tín hiệu ra
{y k }, k=0,1, từ tín hiệu vo {u k }, k=0,1, v các trạng thái đầu y 0 , y 1 , , y n 1
cho trớc. Vì tín hiệu vora l causal nên phải có u k =0, y k =0 khi k<0.
1)

Phơng pháp trực tiếp: Từ (2.1) ta có ngay công thức lặp để tính y k , k=n,n+1,
nh sau:
yk = b0uk + b1uk 1 +

2)

+ bmuk m ( a1 yk 1 +

+ an yk n )

Phơng pháp gián tiếp: Do phơng trình sai phân (2.1) l tuyến tính nên nghiệm
{y k } của nó sẽ l tổng của hai thnh phần gồm nghiệm phơng trình thuần nhất,
còn gọi l đáp ứng tự do, v nghiệm riêng, gọi l đáp ứng cỡng bức.
a)

Đáp ứng tự do: L nghiệm của
yk + a1 yk 1 +

+ an yk n = 0 với giá trị đầu y 0 , y 1 , , y n 1

(2.2)

Ký hiệu nghiệm đó l yk = c z k với c l hằng số thì khi thay vo (2.2), sẽ đợc:
c z k n ( zn + a1 zn 1 +

+ an ) = 0 zn + a1 z n 1 +

+ an = 0

(2.3)

Phơng trình (2.3) có tên gọi l đa thức đặc tính của (2.2).
Giả sử (2.3) có n nghiệm z 1 , z 2 , , z n khác nhau đôi một (chú ý rằng chúng
có thể l nghiệm phức, nhng sẽ tạo thnh các cặp liên hợp). Khi đó nghiệm
thuần nhất của (2.2) sẽ l:
yk = c1 z1k + c1 z2k +

+ cn znk

(2.4)

Trờng hợp phơng trình đặc tính (2.3) có nghiệm bội, chẳng hạn có nghiệm z i
bội q, thì thnh phần ci zik tơng ứng trong (2.4) sẽ đợc thay bởi:
zik ( ci,1 + ci,2 k +

+ ci,q kq 1 )

(2.5)

Các hằng số c 1 , c 2 , , c n trong (2.4) cũng nh c i,1 , c i,2 , , c i,q trong (2.5)
sẽ đợc xác định từ n trạng thái đầu y 0 , y 1 , , y n 1 cho trớc. ở cả hai
trờng hợp luôn có n hằng số cần phải xác định từ n giá trị đầu.
b)

Đáp ứng cỡng bức: L một nghiệm riêng của (2.1) ứng với trạng thái đầu bằng
0. Nghiệm riêng ny thờng đợc tìm bằng cách giả định trớc cấu trúc của y k
theo u k đã biết nhng với tham số bất định. Sau đó ta sẽ xác định các tham số
đó bằng cách thay vo (2.1) rồi cân bằng hệ số của hai vế. Bảng sau giới thiệu
một số cấu trúc của y k với A v Ai l tham số cha biết, đợc chọn theo u k :

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

5


u k =d

y k =dA

u k =dk

y k =dAk

u k =d k

u k =Ad k

u k =d k cos(k )

yk = A1 A2k cos( k + A3 )

u k =d k sin(k )

yk = A1 A2k sin( k + A3 )

uk = d k ci ki

c)

p

i=0

p

yk = d k Ai ki
i=0

Nghiệm chung: Nghiệm của (2.1) tìm theo phơng pháp gián tiếp sẽ l tổng
của nghiệm thuần nhất (2.4), tức l quá trình tự do v một nghiệm riêng (quá
trình cỡng bức) đợc tìm từ b).

Hệ liên tục: Không mất tính tổng quát nếu ta cho rằng mô hình vora (1.4) của hệ
SISO, nhân quả, liên tục, tuyến tính tham số hằng, l:
a0 y + a1 y(1) + a2 y(2) + + an 1 y( n 1) + y( n ) = b0u + b1u(1) + + bnu( n )

(2.6)

Bi toán xác định đáp ứng cho hệ (2.6) đợc hiểu l tìm nghiệm y(t) của phơng trình
vi phân tuyến tính tham số hằng (2.6) khi biết trớc u(t), tức l khi biết trớc vế
phải, v n giá trị đầu y(0), y(1) (0),

, y( n 1) (0) . Do (2.6) l tuyến tính nên nghiệm y(t)

của nó sẽ l tổng của hai thnh phần gồm nghiệm thuần nhất (có vế phải bằng 0 cùng
các giá trị đầu cho trớc), còn gọi l đáp ứng tự do, v một nghiệm riêng của (2.6) có
vế phải u( t ) = b0u( t ) + b1u(1) ( t ) + + bnu( n ) ( t ) đã biết, đợc xác định từ u(t) đã cho v
các giá trị đầu bằng 0, gọi l đáp ứng cỡng bức.
1)

Đáp ứng tự do: L nghiệm của
a0 y + a1 y(1) + a2 y(2) + + an 1 y( n 1) + y( n ) = 0

Đặt y = c e t sẽ có:
c e t ( a0 + a1 + + an 1 n 1 + n ) = 0

a0 + a1 + + an 1 n 1 + n = 0

(2.7)

Phơng trình (2.7) có tên l phơng trình đặc tính của (2.6). Nếu (2.7) có n
nghiệm 1 , 2 , , n khác nhau đôi một, thì nghiệm thuần nhất của (2.6) sẽ l:
y( t ) = c1 e1 t + c1 e2 t +

+ cn en t

(2.8)

Trờng hợp phơng trình đặc tính (2.3) có nghiệm bội, chẳng hạn có nghiệm i

bội q, thì thnh phần ci ei t tơng ứng trong (2.8) sẽ đợc thay bởi:
ei t ( ci,1 + ci,2 t +

+ ci,q t q 1 )

(2.9)

Các hằng số c 1 , c 2 , , c n trong (2.8) cũng nh c i,1 , c i,2 , , c i,q trong (2.9) sẽ
đợc xác định từ n trạng thái đầu y(0), y(1) (0),
2)

, y( n 1) (0) cho trớc.

Đáp ứng cỡng bức: L một nghiệm riêng của (2.6) ứng với các trạng thái đầu
bằng 0 v vế phải u( t ) khác 0. Nghiệm riêng ny đợc tìm bằng cách giả định
trớc cấu trúc của y(t) theo u( t ) đã biết nhng với tham số không biết trớc. Sau
đó thay vo (2.6) rồi cân bằng hệ số của hai vế để có các tham số ny.

6

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


Bảng sau l một số dạng đặc biệt của y(t) đợc chọn theo u( t ) cho hệ bậc 2
(n=2), trong đó A v Ai l tham số cha biết cần đợc xác định:

u=

y=

m

i =0

citi

i =0

m

Aiti (khi a 0 0)

y=

m +1

u = d ect

y = A ect

u = d sin( ct + )

y = A1 sin( ct + A2 )

Ait (khi a 0 =0)

i

i=0

u = d cos( ct + )

y = A1 cos( ct + A2 )

Mô hình đáp ứng xung:
1)

Xét hệ không liên tục (2.1). Ký hiệu {g k }, k=0,1, l tín hiệu ra khi tín hiệu vo
có dạng dãy xung { k }={1,0,0, } v hệ đang ở trạng thái đầu bằng 0. Do mọi
dãy giá trị tín hiệu vo {u k }, k=0,1, bất kỳ luôn biểu diễn đợc dới dạng tổng
tuyến tính:
uk =



ui k i , k=0,1,

i=0

v hệ (2.1) l tuyến tính, nên tín hiệu ra {y k }, k=0,1, tơng ứng cũng sẽ l:
yk =



ui gk i , k=0,1,

(2.10)

i =0

Nói cách khác, dãy giá trị đáp ứng xung {g k }, k=0,1, l một mô hình mô tả hệ
(2.1), nó cho phép ta xác định đợc tín hiệu ra {y k }, k=0,1, từ tín hiệu vo
{u k }, k=0,1, khi hệ có trạng thái đầu bằng 0, theo công thức tích chập (2.10)
Dãy giá trị đáp ứng xung ny còn đợc gọi l dãy giá trị hm trọng lợng để nhấn
mạnh tính chất mô hình của nó.
2)

Tơng tự ta xét hệ liên tục (2.6) v gọi g(t) l đáp ứng của nó với hm xung dirac

(t) khi hệ có trạng thái đầu bằng 0. Vì mọi tín hiệu vo u(t) bất kỳ no khác
luôn có dạng tổng tuyến tính (1.1) các hm xung diract, tức l:


u( t ) = u( ) ( t )d
0

v hệ (2.6) l tuyến tính, nên tín hiệu ra tơng ứng của nó cũng sẽ l:


y( t ) = u( ) g( t )d = u( t ) * g( t )

(2.11)

0

Vậy đáp ứng xung g(t) của hệ (2.6) l một mô hình. Nó cho phép ta xác định đợc

tín hiệu ra y(t) từ tín hiệu vo u(t) khi hệ có trạng thái đầu bằng 0, theo công
thức tích chập (2.11). Cũng vì lý do đó, hm đáp ứng xung ny còn đợc gọi l
hm trọng lợng của hệ.
Chú ý: Vì xung dirac (t) không mang bản chất của một hm thờng, tức l không

phải l một tín hiệu, nên ta cũng không thể xác định đợc hm trọng lợng g(t)
theo những phơng pháp trực tiếp trên miền thời gian.

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

7


Bi tập:
1)

Tìm đáp ứng cho hệ 4 yk 6 yk 1 + 3 yk 2 = uk khi đầu vo l dãy giá trị trích mẫu
của tín hiệu 1(t) v các giá trị đầu l y 0 =1, y 1 =1.

2)

Tìm đáp ứng cho hệ y + y(2) = u u(1) khi tín hiệu đầu vo l u = 2t + sin(3t ) v
các trạng thái đầu l y(0)=1, y (1) (0)=1.

2.2

Mô hình trạng thái hệ liên tục

Với ký hiệu phép tính đạo hm pk =

(a

0



dk
dt k

thì mô hình vora (2.6) viết đợc thnh:

) (

)

+ a1 p + + an 1 pn 1 + pn y = b0 + b1 p + + bn pn u

G( p ) =

b0 + b1 p + + bn p
y
B( p)
=
=
u a0 + a1 p + + an 1 pn 1 + pn
A( p)
n

trong đó A ( p ) l đa thức mẫu số, B ( p ) l đa thức tử số của G ( p ). Đặt biến mới:
u

u
u
, x2 = p
,
, xn = pn 1
x1 =
A( p)
A( p)
A( p)
ta có px 1 = x 2 , , px n 1 = x n v A ( p ) x 1 = u , tức l a 0 x 1 + a 1 x 2 + + a n 1 x n + px n = u , hay
0

0
dx
=
px =
dt
0
a
0

1

0

0

1

0

0

a1

a2


0

x1


x + u = Ax + Bu với x =

0

x
1

n
1


an 1
0

0

(2.12)

Ngoi ra, ta còn có:
u( b0 + b1 p + + bn pn )
= b0 x1 + b1 x2 + + bn 1 xn + bn pxn
A( p)
= ( b0 a0bn ) x1 + ( b1 a1bn ) x2 + + ( bn 1 an 1bn ) xn + bnu

y=

= ( b0 a0bn , b1 a1bn ,

, bn 1 an 1bn ) x + bnu = Cx + Du

(2.13)

Nh vậy, hai phơng trình (2.12), (2.13) đã tạo thnh mô hình trạng thái (1.6) cho hệ
SISO nhân quả, liên tục, tuyến tính, tham số hằng có mô hình vora (2.6). Phơng
trình trạng thái ny có A l ma trận nìn , B l vector cột, C l vector hng v D l hằng
số thực.
Một cách tổng quát thì mô hình trạng thái hệ tuyến tính, liên tục có dạng:
dx
= Ax + Bu v y = Cx + Du
dt

(2.14)

trong đó u = (u1 , , um )T l vector các tín hiệu vo, y = ( y1 , , y p )T l vector tín hiệu ra,
x = ( x1 , , xn )T l vector trạng thái, A R

nìn

, B R n

ìm

, C R p

ìn

, D R p

ìm

, l các ma

trận có số chiều tơng ứng.

8

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


ở hệ không dừng, các ma trận A , B , C , D trong (2.14) sẽ phụ thuộc thời gian, còn ở
hệ tham số rải các ma trận ny sẽ phụ thuộc tham số không gian. Nghiệm tổng quát của

(2.14) với giá trị đầu x (0)= x 0 l:
t

t

0

0

x( t ) = e At x0 + e A( t ) Bu( )d v y( t ) = Ce At x0 + C e A( t ) Bu( )d + Du

trong đó
e At =



( At )k
(đợc gọi l ma trận hm mũ).
k=0 k !



Bi tập:
Hãy viết mô hình trạng thái của hệ có mô hình vora y(2) = u v tìm đáp ứng khi
tín hiệu vo l u( t ) = t sin(2t ) v trạng thái đầu l y(0)= y (1) (0)=1.
2.3

Mô hình trạng thái hệ không liên tục

Tơng tự nh đã lm với hệ liên tục m ở đó mô hình trạng thái (2.12), (2.13) đợc
dẫn ra từ mô hình vora (2.6), thì ở đây, từ mô hình vora (2.1) của hệ không liên tục,
sau khi bổ sung các hệ số bm +1 = = bn = 0 , cũng nh ký hiệu z yk = yk +1 chỉ phép tính
dịch trục v n giá trị trạng thái:
xk,1 =

uk
z uk
zn 1 uk
với A( z ) = zn + a1 z n 1 + + an
, xk,2 =
, , xk,n =
A( z )
A( z )
A( z )

ta sẽ có mô hình trạng thái (1.7) tơng đơng:
x k +1 = Ax k + Buk v y = Cx k + Duk

(2.15)

k

với
1
0
0

0
1
0
A=

0
0
0

a a
n 1 an 2
n
C = ( bn anb0 , bn 1 an 1b0 ,

0
xk,1
0



0

x
, B = , x = k,2


k
0



1

xk,n
1

a1
, b1 a1b0 ) , D = b0

Một cách tổng quát thì mô hình trạng thái hệ MIMO tuyến tính, không liên tục có dạng:
x k +1 = Ax k + Bu k v y = Cx k + Duk

(2.16)

k

trong đó uk = (uk,1 , , uk,m )T l vector các tín hiệu vo, y = ( yk,1 , , yk, p )T l vector tín
k

hiệu ra, x k = ( xk,1 , , xk,n )

T

l vector trạng thái, A R

nìn

, B R n

ìm

, C R p

ìn

, D R p

ìm

,

l các ma trận có số chiều tơng ứng. Từ phơng trình trạng thái (2.16) ta có đợc ngay
công thức lặp để xác định x k , y :
k

x k = A k x0 +

k 1



k 1



i=0



i=0



A k i1 Bui , yk = C A k x0 + A k i1 Bui + Duk

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

(2.17)

9


3

Chuỗi Fourier và phép biến đổi Fourier

3.1

Chuỗi Fourier

Bi toán: Cho hm x(t). Với điều kiện no thì phân tích nó đợc thnh chuỗi:
x( t ) = a0 +

n

n

k =1

k =

ak cos( k t ) + bk sin( k t ) = ck e j t

(3.1)

2

, e j = cos + j sin (công thức Euler), c k = ck (số phức liên hợp) v
T
T l hằng số dơng.

trong đó =

Trả lời:
1)

Hm x(t) phải tuần hon với chu kỳ T, vì vế phải l hm tuần hon với chu kỳ T.

2)

Hm x(t) phải liên tục từng đoạn v tại điểm không liên tục t 0 phải có:
x( t0 ) =

1
x( t0 0) + x( t0 + 0)
2

Đây l điều kiện để dấu bằng cũng đúng tại t 0 .
3)

Dirichlet: Điều kiện đủ để chuỗi Fourier (3.1) ở vế phải hội tụ l:
Nếu khoảng ( 0 , T ) chia đợc thnh hữu hạn các khoảng con sao cho hm x(t) l
liên tục, đơn điệu trong các khoảng con đó.
Một cách nói khác: Nếu hm x(t) chỉ có hữu hạn các điểm không liên tục v cũng
chỉ có hữu hạn các điểm cực trị.
Chú ý: Điều kiện Dirichlet chỉ l điều kiện đủ (ví dụ minh họa của Weirstrass).
Cha có điều kiện cần v đủ.

4)

Chuỗi ở vế phải trong (3.1) còn l hội tụ đều nếu có:




k =1

k=0

( ak + bk ) < , cũng nh ck <

tức l khi đó giới hạn x(t) của chuỗi (3.1) cũng l hm liên tục, khả vi, khả tích
giống nh các phần tử của chuỗi.
Khai triển chuỗi: Các hệ số thực a k , b k , k=,0,1, v hệ số phức c k , k=,1,0,1,
trong chuỗi (3.1) đợc xác định từ x(t) theo:
a0 =

1
T

T

ck =

1
T

T

2

T

2

T

x( t )dt , ak = T x( t ) cos( k t )dt , bk = T x( t )sin( k t )dt , k = 1,2, (3.2)
0
0
0

x( t )e

jk t

dt , k = , 1 , 0 , 1 , v ck =

0

1
( ak + jbk ) , c0 = a0
2

(3.3)

Tính chất:

10

1)

Nếu x(t) l hm lẻ thì a k =0, k

2)

Nếu x(t) l hm chẵn thì b k =0, k=1,2,

3)

Nếu có x( t +

T
) = x( t ), t thì a 0 =a 2 =a 4 = =b 2 =b 4 = =0
2

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


4)

Bình phơng sai lệch
Q=

T

( x( t ) y( t )) dt

2

0

giữa hm x(t) v y(t) xác định bởi
y( t ) = a0 +

n

( ak cos( k t ) + bk sin( k t ))

k =1

sẽ l nhỏ nhất, nếu y(t) có các hệ số ak , bk đợc tính từ x(t) theo (3.2):
ý nghĩa ứng dụng:
1)

Thnh phần
a1 cos( t ) + b1 sin( t ) = A1 cos( t 1 ) với A1 = a12 + b12 v 1 = arctan

b1
a1

đợc gọi l đơn hi của x(t). Các thnh phần
ak cos( k t ) + bk sin( k t ) = Ak cos( k t k ) , Ak = ak2 + bk2 , k = arctan

bk
, k >1
ak

gọi l đa hi của x(t). Phân tích đơn hi v đa hi đợc sử dụng nhiều trong các
ngnh thuộc lĩnh vực điều khiển truyền tải điện v điện tử công suất, cũng nh
phân tích các dao động điều hòa thnh phần của tín hiệu tuần hon trong các quá
trình vật lý âm học, nhiệt học, điện, cơ
2)

Tìm nghiệm tuần hon của một số phơng trình vi phân đạo hm riêng mô tả quá
trình truyền sóng, truyền nhiệt.

3)

Lọc nhiễu với tần số xác định có trong tín hiệu tuần hon x(t).

4)

Phân tích sự giao thoa các đáp ứng xung trong hệ tuyến tính.

5)

Xấp xỉ một tín hiệu x(t) tuần hon, liên tục từng đoạn bằng tổng hữu hạn các
hm điều hòa:
x( t ) = a0 +

n

( ak cos( k t ) + bk sin( k t ))

k =1

Chú ý rằng khi đó, xung quanh điểm không liên tục t0 của x(t), tổng hữu hạn ở vế

phải vẫn l một hm liên tục với các thnh phần dao động có biên độ lớn. Tổng
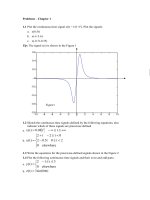
các số hạng n cng lớn, biên độ dao động ny cng lớn. Hiện tợng đó đợc gọi l
hiện tợng Gibb (hình 3.1).
6)

Thiết kế tín hiệu tuần hon x(t) với dải tần số lm
việc cho trớc.

7)

Với tín hiệu không liên tục {x k }, k=,1,0,1,,
trong đó x k =x(kT a ) v T a l chu kỳ trích mẫu đợc
suy ra từ tín hiệu liên tục x(t), thì từ N giá trị trích
mẫu x 0 , x 1 ,, x N 1 có đợc trong một chu kỳ T,
(NT a =T) các hệ số Fourier trong (3.1) sẽ đợc tính
theo:

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

Hình 3.1: Hiện tợng Gibb

11


a0 =
ck =

1
N

N 1

xi , ak =

i=0

N 1

1
xi e
N i =0

j

2 ki
N

2
N

N 1

xi cos( k

i=0

2 i
2
) , bk =

N
N

N 1

xi sin( k

i=0

2 i
) , k = 1,2,
N

, k=,1,0,1,

(3.4)

Các công thức ny đợc suy ra từ (3.2), (3.3) bằng cách thay dấu tích phân bằng
iT
T
v dt bởi Ta =
. Chúng đợc gọi l chuỗi Fourier
dấu tổng , t bằng iTa =
N
N
rời rạc (DFS Discret Fourier Series). Nói cách khác, bản chất của DFS chính l
chuỗi Fourier (3.1) đợc áp dụng cho tín hiệu không liên tục. Chú ý: Tên gọi rời
rạc ở đây không liên quan tới tính chất miền giá trị của ánh xạ (3.1) nh đã định
nghĩa cho tín hiệu. Để chặt chẽ, ta nên gọi nó l chuỗi Fourier cho tín hiệu không
liên tục thay vì chuỗi Fourier rời rạc.

Bi tập:
1)

Chứng minh các công thức (3.2), (3.3).

2)

Hãy xác định chuỗi Fourier của tín hiệu tuần hon x(t) với chu kỳ T=2 v

3)

a) x( t ) = sgn( t ) , 0 < t < 2

b) x( t ) = sin t

t
c) x( t ) = sat
, 0 < t < 2


d) x( t ) = cos2 t


Chứng minh bất đẳng thức Bessel: ck
k =

2

1T
2
x( t ) dt
T 0

n

Gợi ý: Đặt zn ( t ) = x( t ) ck e jk t v đi từ 0 zn ( t ) = zn ( t ) zn ( t )
2

k = n

4)
3.2

Chứng minh hệ quả của Bessel: a02 +

(

)

1
1
ak2 + bk2
2 k =0
T

T

2

x( t ) dt

0

Phép biến đổi Fourier (toán tử Fourier)

Cho hm x(t). ảnh Fourier của nó, ký hiệu bởi X ( j ) đợc định nghĩa l:
X ( j ) =



1



j t
j t
x( t )e dt với ảnh ngợc x( t ) = 2 X ( j )e d

(3.5)





Đây l dạng công thức (3.3) của Euler đợc mở rộng cho cả các tín hiệu x(t) không tuần
hon. ánh xạ:
F : x( t )

X ( j ) =

j t
1
x( t )e dt với F : X ( j )



x( t ) =

1
2



j t
X ( j )e d



đợc gọi l phép biến đổi Fourier v thờng đợc viết thnh:
F { x( t )} = X ( j ) cũng nh F 1 { X ( j )} = x( t )

Câu hỏi: Hm x(t) phải thỏa mãn điều kiện gì thì mới có ảnh Fourier X(j )?

12

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội

Trả lời:
1)

(Điều kiện đủ để tồn tại ảnh Fourier) Hm x(t) phải có chuẩn bậc 1, tức l tích
phân vô hạn thứ nhất trong (3.5) phải hội tụ, hay tín hiệu x(t) có công suất hữu
hạn:


x( t ) dt < , hay x(t)L1



2)

Nếu x(t) không liên tục tại t 0 thì để ảnh ngợc ở công thức thứ hai trong (3.5)
cũng đúng tại t 0 , hm x(t) phải có giá trị tại t 0 l:
x( t0 ) =

1
x( t0 0) + x( t0 + 0)
2

Tính chất:
1)

Nếu x(t) l hm chẵn thì X(j ) l hm thuần thực (phần ảo bằng 0) v nếu x(t)
l hm lẻ thì X(j ) l hm thuần ảo (phần thực bằng 0).

2)

Nếu x(t) có ảnh Fourier X(j ) thì:
a)

y(t)=x(t ) sẽ có ảnh Y ( j ) = X ( j )e j

b)

y( t ) =

dx( t )
sẽ có ảnh Y ( j ) = j X ( j )
dt
n

3)

Phép biến đổi Fourier l tuyến tính: F { ai xi ( t )} =
i =1

n

aiF { xi ( t )} , a i R

i =1

4)

Phép biến đổi Fourier l nội xạ (injective): x(t)y(t) F {x(t)} F {y(t)}

5)

Nếu có x( t ) = x( t ) thì cũng có X ( j ) = X ( j ) , trong đó a l ký hiệu chỉ số phức
liên hợp của a.

6)

Phép tính tích chập của hai hm x(t), y(t) định nghĩa bởi:
z( t ) = x( t ) * y( t ) =



x( ) y( t )d



l đóng trong không gian L 1 . Bởi vậy nếu hai hm x(t), y(t) đã có ảnh Fourier
X(j ), Y(j ) thì tích chập z(t) của nó cũng có ảnh Fourier Z(j ) v
Z( j ) = F { x( t ) * y( t )} = F { x( t )} F { y( t )} = X ( j )Y ( j )

7)

ảnh của một tích bằng tích chập của hai ảnh:
1
1
Z( j ) = F { x( t ) y( t )} =
F { x( t )} * F { y( t )} =
X ( j ) * Y ( j )
2
2

(3.6)

(3.7)

Chú ý: Do phép nhân x(t)y(t) không đóng trong L 1 , nên mặc dù hai hm x(t),

y(t) đã có ảnh X(j ), Y(j ) song có thể tích của chúng lại không có ảnh Fourier.
8)

Parseval: Giữa năng lợng tín hiệu x(t) v ảnh Fourier X(j ) của nó có quan hệ:

1
2
2
x( t ) dt = 2 X ( j ) d



Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

13


9)

RiemannLebesgue: ảnh Fourier X(j ) l hm liên tục theo v lim X ( j = 0 .


10) Chuỗi Fourier (3.1) l trờng hợp riêng của phép biến đổi Fourier (3.5):

Nếu hm x(t) l tuần hon với chu kỳ T, tức l x(t+T)=x(t), t, thì ảnh Fourier
2
X(j ) của nó sẽ l dãy các giá trị 2 {, c 1 , c 0 , c 1 , } xác định tại = n
,
T
n=, 1,0,1, , trong đó cn đợc tính theo công thức (3.3), tức l:

2
X ( j ) = 2 cn ( n
)
T
n =

(3.8)

ý nghĩa ứng dụng:
1)

áp dụng (3.5) để tính ảnh Fourier của xung dirac (t) ta có với định nghĩa (1.1):
F { (t)} =



j t
j 0
=1
( t )e dt = e

Suy ra

( t ) = F 1 {1} =

1
2



1



1

a

j t
e d = 2 cos( t )d = alim
cos( t )d
2





a

sin( at )
= lim

a
t
2)

ảnh Fourier S(j ) của hm trích mẫu (1.2) trong miền thời gian cũng l hm
trích mẫu trong miền tần số:

S( j ) =

2
Ta



( n

n =

2
)
Ta

(3.9)

trong đó Ta l chu kỳ trích mẫu trong miền thời gian.
3)

Khảo sát đặc tính tần số của một tín hiệu (không tuần hon) để biết đợc dải tần
số lm việc của tín hiệu đó. Chẳng hạn nếu có X ( j ) = 0 khi thì tín hiệu
x(t) sẽ không lm việc ở các tần số .

4)

Lọc nhiễu. Ví dụ nếu tín hiệu x(t) có dải tần số lm việc l [ 1 , 2 ] v bị lẫn
nhiễu n(t) lm việc ở các tần số [ 1 , 2 ] theo phép cộng x( t ) = x( t ) + n( t ) thì
ta sẽ lọc đợc nhiễu n(t) ra khỏi x( t ) để có lại tín hiệu hữu dụng x(t) theo quy
trình:

{

}

x( t ) = F 1 F { x( t )} 1( 1 ) 1( 2 )
5)

Thiết kế tín hiệu x(t) có dải tần số lm việc mong muốn.

6)

Tìm nghiệm của một số phơng trình vi phân đạo hm riêng nh phơng trình
Laplace, phơng trình truyền sóng, truyền nhiệt.

7)

ảnh X a (j ) của tín hiệu không liên tục {x k }, k=,1,0,1, l:

X a ( j ) = Ta

14

(3.10)



j kTa
xk e

(3.11)

k =

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


Nó đợc suy ra từ (3.5) bằng cách thay dấu tích phân bằng dấu tổng , t bằng
kT
T
v dt bởi Ta =
. Chúng đợc gọi l phép biến đổi Fourier rời rạc
kTa =
N
N
(DFT Discret Fourier Transformation). Nói cách khác DFT l phép biến đổi
Fourier (3.5) cho tín hiệu không liên tục. Chú ý: Tên gọi ny không liên quan tới
miền giá trị của phép biến đổi đó, tức l ảnh X a (j ) của phép biến đổi Fourier rời
rạc vẫn có thể có miền giá trị l các tập liên thông trên trờng số phức. Để chặt
chẽ, tên gọi đúng của phép biến đổi Fourier rời rạc phải l phép biến đổi Fourier
cho tín hiệu không liên tục.
8)

Hiện tợng trùng phổ: Xem tín hiệu không liên tục {x k }, k=,1,0,1, l hm
mở rộng x( t ) =x(t)s(t) thì ảnh X ( j ) của nó sẽ l:
Ta X ( j ) =



X ( j ( n

n =

2
))
Ta

(3.12)

Giữa X ( j ) v X a (j ) trong (3.11) còn có quan hệ Ta X ( j ) = X a ( j ) . Công thức
(3.12) đợc gọi công thức trùng phổ. Từ công thức trùng phổ đó ta còn suy ra ngay
đợc định lý ShannonKatelnikov phát biểu nh sau (hình 3.2):
Nếu X(j )=0 khi [,] thì với T a thỏa mãn Ta <




, ta sẽ có X(j )=X a (j )

khi [,].
Bi tập:
1)

Chứng minh các công thức (3.6), (3.7), (3.8), (3.9), (3.12) v Ta X ( j ) = X a ( j ) .

2)

Cho x(t)=1(t+T)1(tT). Tìm ảnh X(j ) v

3)

a)

kiểm tra tính chất của nó nêu trong định lý RiemannLebesgue,

b)

kiểm tra quan hệ Parseval.

Cho x(t) tuần hon với chu kỳ T. Ký hiệu s(t) l hm trích mẫu có cùng chu kỳ
trích mẫu T v x( t ) = x( t ) 1( t ) 1( t T ) l hm lấy từ x(t) chỉ trong một chu kỳ.
Chứng minh rằng x( t ) = x( t ) * s( t ) , từ đó xác định X(j ).

4)

Chứng minh rằng ảnh X a (j ) của dãy
vô hạn {x k }, k=,1,0,1,, xác định
theo công thức (3.11), l hm tuần
2
hon với chu kỳ
.
Ta

5)

Từ kết quả bi 3) v công thức trùng
phổ (3.12) của phép biến đổi Fourier,
hãy xây dựng công thức trùng phổ cho
chuỗi Fourier.

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

Hình 3.2: Minh họa hiện tợng trùng phổ.

15


4

Đáp ứng tần số và lọc tín hiệu

4.1

Đặc tính tần số v đồ thị hm đặc tính tần

Xét hệ tuyến tính có tín hiệu vo l u(t) v tín hiệu ra l y(t). Giả sử hệ có tính
chất l với u(t)L1 cũng sẽ có y(t)L1 hoặc cả hai tín hiệu vo ra đều cùng có ảnh
Fourier. Gọi U(j ), Y(j ) l ảnh Fourier của u(t), y(t), trong đó y(t) l đáp ứng của hệ
từ trạng thái đầu bằng 0. Khi đó hm đặc tính tần đợc hiểu l:
G( j ) =

Y ( j )
U ( j ) trạng thái đầu = 0

(4.1)

Mô hình: Hm đặc tính tần định nghĩa bởi (4.1) l một mô hình mô tả hệ tuyến tính
tham số hằng, vì từ tính xếp chồng của hệ u1
y1 , u2
y2 u1 + u2
y1 + y2 ,
cũng nh tính chất tuyến tính của phép biến đổi Fourier ta có:
GU = Y G(U1 + U2 ) = Y1 + Y2 = G1U1 + G2U2 , U1 , U2 G = G1 = G2
tức l tỷ số (4.1) luôn bất biến với tín hiệu vo. Suy ra:
y( t ) = F 1 {G( j )U ( j )} = F 1 {G( j )F {u( t )}}

G : u( t )

(4.2)

Đồ thị hm đặc tính tần: Từ 2 dạng khác nhau biểu diễn một số phức:
G( j ) = Re{G( j )} + j Im{G( j )} = G( j ) e jarcG( j )
trong đó Re{G(j )} l phần thực, Im{G(j )} l phần ảo, cũng nh G( j ) l modun
v arcG(j ) l góc pha của số phức đó, nói cách khác:

G( j ) =

( Re{G( j )} )

2

+ ( Im{G( j )} )

2

v arcG( j ) = arctan

Im{G( j )}
Re{ G( j )}

ta sẽ có hai cách biểu diễn G(j ) dới dạng đồ thị nh sau:
1)

Đồ thị biênpha (hay đồ thị Nyquist): L đồ thị phụ thuộc tham số của
G(j ) trong mặt phẳng phức có trục honh Re{G(j )} v trục tung Im{G(j )}.
Nếu tín hiệu vora của hệ thỏa mãn u( t ) = u( t ), y( t ) = y( t ) , ví dụ chúng đều l
các tín hiệu có giá trị thực, thì do
G( j ) = G( j ) , nên đồ thị sẽ có dạng
đối xứng qua trục thực (trục honh). Bởi
vậy, ta chỉ cần vẽ đồ thị với 0 l
đủ. Hình 4.1 l một ví dụ về đồ thị
biênpha cho hệ có hm đặc tính tần:
G( j ) =

k
1 T 2 2 + j 2TD

ứng với các giá trị D khác nhau. Đồ thị
1
cắt trục ảo (trục tung) khi c =
v
T
xuất phát tại điểm k trên trục thực.

16

Im{G}

Re{G}

=0

( )
|G(j )|

c

D=1.0

D=0.5
D=2.0

Hình 4.1: Đồ thị biênpha (Nyquist)

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


L( )

( )

D=0.1

D=0.1


D=1.5

D=2.0

D=1.5
D=2.0
1

10

100

1

100

10

Hình 4.2: Đồ thị Bode (logarith)

2)

Đồ thị Bode (logarith): Gồm hai đồ thị phụ thuộc tham số 0 l:
L( ) = 20 lg G( j ) v ( ) = arcG( j )

Cả hai đồ thị đều có giá trị l số thực v có trục honh đợc chia tỷ lệ theo lg .
Với việc chia tỷ lệ nh vậy ta có thể dễ dng xây dựng đồ thị Bode cho hệ gồm
nhiều hệ con mắc nối tiếp bằng cách cộng các đồ thị thnh phần, vì:
m

G( j ) = Gi ( j ) L( ) =
i =1

m

m

i =1

i =1

Li ( ) v ( ) = i ( )

Hình 4.2 biểu diễn minh họa đồ thị Bode của hm đặc tính tần có đồ thị biênpha
cho ở hình 4.1.
4.2

Đáp ứng tần số v quan hệ với đáp ứng thời gian

ở hệ tuyến tính tham số hằng mô tả bởi hm đặc tính tần (4.1) thì đáp ứng y(t) ở
đầu ra sẽ đợc xác định từ kích thích u(t) ở đầu vo nhờ (4.2) v đó cũng l công thức
biểu diễn quan hệ giữa đáp ứng tần số Y(j )=G(j )U(j ) v đáp ứng thời gian y(t).

Xét riêng trờng hợp u(t) l tín hiệu tuần hon với chu kỳ T. Từ (3.8) ta có ảnh
Fourier U(j ) của u(t). Suy ra ảnh Fourier Y(j ) của y(t) sẽ l:

n =

n =

cn ( n0 )G( j ) = 2 cnG( jn0 ) ( n0 ) với 0 =

Y ( j ) = 2



= 2

cn ( n0 ) trong đó cn = cnG( jn0 ) v cn =

n =

Vậy:

y( t ) =
=
=

1
2

1
T

T

u( t )e

2
T

jn0 t

dt

0



j t
j t
Y ( j )e d = cn ( n0 )e d
n =

n =



n =

cnG( jn0 ) ( n0 )e j t d = cnG( jn0 )e jn0 t


dn e jn0 t với dn = cnG( jn0 )

n =

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

17


Điều đó nói rằng tín hiệu ra y(t) cũng tuần hon với chu kỳ T v d n , n=,1,0,1, l
các hệ số chuỗi Fourier của nó, tức l:
dn =

1
T

T

y( t )e

jn0 t

dt , n = , 1 , 0 , 1 ,

(4.3)

0

Từ đây ta đi đến các bớc thực nghiệm để xây dựng hm đặc tính tần nh sau:
1)

Thiết kế tín hiệu u(t) tuần hon với chu kỳ T chọn trớc có dải tần số lm việc đủ
lớn v xác định các hệ số chuỗi Fourier c n , n=,1,0,1, của nó theo:
cn =

1
T

T

u( t )e

jn0 t

dt , n = , 1 , 0 , 1 ,

0

Ta cũng có thể chọn trớc hai dãy giá trị thực a k , k=0,1, v b k , k=1,2, rồi
thiết kế u(t) tuần hon với chu kỳ T theo:
u( t ) = a0 +

n

ak cos( k0 t ) + bk sin( k0 t ) trong đó 0 =

k =1

2
T

(4.4)

Khi đó các hệ số phức c n , n=,1,0,1, sẽ l
c0 = a0 , cn =

1
( an + jbn ) , n = 1,2,
2

2)

Kích thích hệ ở đầu vo bằng tín hiệu u(t) vừa đợc thiết kế rồi đo tín hiệu y(t)
cũng tuần hon với chu kỳ T ở đầu ra.

3)

Tính các hệ số chuỗi Fourier d n , n=,1,0,1, của y(t) theo (4.3). Nếu kết quả
đo đợc ở bớc 2) chỉ l dãy gồm N giá trị y 0 , y 1 ,, y N 1 trong một chu kỳ, thì
các hệ số d n , n=,1,0,1, sẽ đợc tính xấp xỉ nhờ công thức DFS (3.4), tức l:
dn =

1 N 1 j
yi e
N i =0

2 ni
N

, n=,1,0,1,

(4.5)

Chú ý rằng do d n theo (4.5) l tuần hon với chu kỳ N nên ở đây, trong công thức

(4.5) ta chỉ cần tính N giá trị của nó trong một chu kỳ d n , n=0,1,,N1 l đủ.
4)

Tính các giá trị của hm đặc tính tần:
d
G( jn0 ) = n , n = , 1,0,1,
cn
rồi biểu diễn chúng dới dạng đồ thị Nyquist hoặc đồ thị Bode (hình 4.1 v 4.2).

Cuối cùng, cũng từ các kết quả phân tích trên, ta còn nhận thấy l khi hệ đợc kích
thích bằng tín hiệu điều hòa:
u(t)=sin( 0 t)

ở đầu vo, thì với (4.4), tức l với a k =0, k v b 2 =b 3 ==0, nên tín hiệu ra sẽ l:
y( t ) = G( j0 ) sin (0 t + (0 )) với (0 ) = arcG( j0 )

(4.6)

v (4.6) sẽ l một gợi ý cho phơng pháp thực nghiệm thứ hai để có hm đặc tính tần.

18

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


4.3

Lọc tín hiệu

Nguyên tắc giải quyết bi toán lọc tín hiệu nhiễu n(t) ra khỏi tín hiệu hữu dụng
x(t) từ tín hiệu đầu cuối z(t)=x(t)+n(t) nh mô tả ở hình 4.3, đã đợc trình by ở mục
3.2 với công thức (3.10). Vấn đề cần giải quyết tiếp ở đây l phải ci đặt đợc công thức
(3.10) đó thnh bộ lọc số khi luôn tồn tại những khó khăn sau:
Không thể có đợc dãy vô hạn các giá trị z k =z(kT a ), k=,1,0,1, của z(t), trong
đó T a l chu kỳ trích mẫu, bằng thực nghiệm.
Với các phơng pháp số, không thể xác định đợc ảnh
Fourier Z(j ) m chỉ có thể có đợc các giá trị Z(jn a ),
n=,1,0,1, của nó. Thậm chí ta cũng chỉ có thể có
đợc hữu hạn các giá trị ny.
Ký hiệu dãy hữu hạn gồm N giá trị đo đợc của tín

n
x

z

Bộ lọc

x

Hình 4.3: Lọc nhiễu tín hiệu

hiệu z(t) l z k , k=0,1,,N1 thì từ (3.11), ta sẽ có:
Za ( j ) = Ta

N 1

j kTa
zk e

(4.7)

k =0

2
. Bởi vậy ta cũng sẽ
Ta
chỉ lấy N các giá trị Z a (jn a ), n=0,1,,N1 của nó trong một chu kỳ. Suy ra:
Với (4.7) ta nhận thấy ngay Z a (j ) l hm tuần hon có chu kỳ

N a =

2

2
a =
Ta
NTa

l chu kỳ trích mẫu trong miền tần số. Điều ny dẫn đến:
Za ( jn a ) = Ta

N 1

zk e

jnk

2
N

, n=0,1,,N1

(4.8)

Za ( jn a ) khi n a [1 , 2 )
Za ( jn a ) = Za ( jn a ) 1( 1 ) 1( 2 ) =
0 khi n a [1 , 2 )

(4.9)

k=0

Thay (4.8) vo (3.10) v để ý rằng:

sẽ có
2

jn
t
N 1
1 N 1
NTa
x( t ) = F { Za ( jn a )} = a Za ( jn a )e jn a t =
Za ( jn a )e
NTa n =0
2 n = 0
1

xk = x( kTa ) =



1
NTa

N 1

Za ( jn a )e

jnk

2
N

,

k=0,1,,N1

(4.10)

n=0

Ba công thức (4.8), (4.9) v (4.10) tạo thnh cơ sở của việc ci đặt bộ lọc tín hiệu số gồm
các bớc nh sau:
1)

Đo N giá trị z k =z(kT a ), k=0,1,,N1 của tín hiệu z(t) v tính N giá trị ảnh
Fourier của nó Z a (jn a ), n=0,1,,N1 theo (4.8).

2)

Tính Za ( jn a ) , n=0,1,,N1 theo (4.9).

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

19


3)

Tính x k =x(kT a ), k=0,1,,N1 của tín hiệu hữu dụng x(t) từ ảnh Za ( jn a ) ,
n=0,1,,N1 theo (4.10).
Ngoi ra, nếu để ý rằng với xk = xk sẽ còn có:

xk = xk =

1
NTa

N 1

Za ( jn a )e

jnk

2
N

n=0

Bởi vậy việc thực hiện công thức (4.10) sẽ hon ton giống nh việc đã thực hiện công
thức (4.8) trớc đó nếu ta thay vai trò của z k trong (4.8) bằng Za ( jn a ) .
Bi tập:
1)

Sử dụng công thức định nghĩa hm đặc tính tần (4.1), hãy xác định hm trọng
lợng g(t) cho các hệ có hm đặc tính tần nh sau:
1
1 + j
1

a) G( j ) =
c) G( j ) =

(1 + j )2

b) G( j ) =
d) G( j ) =

1
(1 + j )(1 + 2 j )
1

(1 + j )2 (1 + 2 j )

2)

Hãy vẽ đồ thị đặc tính tần biênpha v đồ thị Bode cho các hệ có hm đặc tính
tần cho trong bi 1).

3)

Hãy xác định hai đờng tiệm cận của đồ thị Bode L( ) của hệ cho ở bi 1) câu a)
khi =0 v khi cũng nh honh độ giao điểm của chúng. Từ đó nêu lên
phơng pháp xây dựng xấp xỉ đồ thị Bode L( ) cho các hệ còn lại.

4)

Sử dụng kết quả bi 2), hãy xác định đáp ứng đầu ra của những hệ đó, khi đầu
vo l tín hiệu điều ho:
a) u(t)=sin( t )

b) u(t)=sin( t ) + sin( 2 t )

1 t khi t 1
v s(t) l hm trích mẫu chu kỳ 1.
c) u(t)=x(t)*s(t) với x( t ) =
0 khi t > 1

5)

Hãy dựa vo công thức gợi ý (4.6) để xây dựng các bớc xác định hm đặc tính tần
của hệ tuyến tính tham số hằng bằng thực nghiệm.

6)

Hãy dựa vo dạng đồ thị thu đợc từ bi 2) của các hệ có hm đặc tính tần cho ở
bi 1) để chứng minh rằng chúng đều có khả năng lọc đợc nhiễu tần số cao.

7)

Cho dãy vô hạn các giá trị z k =z(kT a ), k=,1,0,1, của tín hiệu z(t). Gọi
Za ( j ) = Ta

N 1



k =0

k =

j kTa
v Za ( j ) = Ta zk e j kTa

zk e

l hai ảnh Fourier xấp xỉ của Z(j ). Sai lệch Za ( j ) Za ( j ) đợc gọi l sai số
rò rỉ (leakage). Chứng minh rằng nếu z(t) l tuần hon với chu kỳ T v NTa=T
thì sai số rò rỉ sẽ bằng 0.

20

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


5

Phép biến đổi Laplace và hàm truyền hệ liên tục

5.1

Phép biến đổi Laplace (toán tử Laplace)

Mở rộng phép biến đổi Fourier (3.5) cho các tín hiệu causal x(t) không cần có chuẩn
bậc 1, tức l x(t)L 1 , ta có phép biến đổi Laplace:
X ( s) =



1

+ j

st

st
x( t )e dt v ảnh ngợc x( t ) = 2 j X ( s)e ds

(5.1)

j

0

trong đó s = + j v l số thực dơng đủ lớn để tồn tại tích phân vô hạn thứ nhất
trong (5.1), nó đợc gọi l bán kính hội tụ của ảnh Laplace X(s). Phép biến đổi Laplcae
trên đợc ký hiệu bởi L{ }, tức l:
X(s)= L {x(t)} v x(t)= L

1

{X(s)}

Để dấu = trong tích phân thứ 2 của (5.1) đúng với mọi t, kể cả tại điểm t 0 không liên tục
của x(t), thì giống nh ở phép biến đổi Fourier, ta cần phải giả thiết thêm:
x( t0 ) =

1
x( t0 0) + x( t0 + 0)
2

(5.2)

Nói rằng (5.1) l sự mở rộng của Fourier (3.5) cho cả những tín hiệu causal x(t)L 1 , vì
khi đó cũng sẽ luôn tồn tại >0 sao cho x( t ) = x( t )e t L1 . Nh vậy ta lại có ảnh

Fourier X ( j ) của tín hiệu causal x( t ) :
X ( j ) =
=



x( t )e

j t

dt =

0




x( t )e

t j t

e

dt =

0



x( t )e

( + j )t

dt

0

st
x( t )e dt = X ( s)

0

x( t ) = e t x( t ) = e t

v

1
2



1



1

+ j

( + j )t

j t
st
d =
X ( j )e d = 2 X ( j )e
X ( s)e ds
2 j j



Tính chất:
1)

Phép biến đổi Laplace có đầy đủ mọi tính chất của phép biến đổi Fourier:
n

a)

Tuyến tính: L{ ai xi ( t )} =
i =1

n

aiL{ xi ( t )} , a i R

i =1

b)

Nội xạ: x(t)y(t) L {x(t)} L {y(t)}

c)

ảnh của tích chập bằng tích của hai ảnh: L {x(t)*x(t)}= L {x(t)} L {y(t)}

d) ảnh X(s) l hm liên tục theo Im(s), khi Re(s)> (ký hiệu Re(s) l chỉ phần
thực v Im(s) l chỉ phần ảo của số phức s).
2)

Gọi X ( s ) l ảnh Laplace của x ( t ) . Khi đó:
a) y(t)=x(t )} có ảnh l Y(s)=X(s)e
b)

y(t)=e

as

s

x(t)} có ảnh l Y(s)=X(s+a)

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

21


c)
d)
e)
f)

y(t)=x(at) có ảnh l

t
1
s
X ( ) v y( t ) = x( ) có ảnh l Y(s)=aX(as)
a
a
a

dx
có ảnh l Y(s)=sX(s)x(+0)
dt
X ( s)
y( t ) = x( t )dt có ảnh l Y ( s) =
s

y( t ) =

y( t ) =


x( t )
có ảnh l Y ( s) = X ( s ')ds '
t
s

3)

Nếu X ( s ) có bán kính hội tụ =0 thì X ( s) s = j = X ( j ) l ảnh Fourier của x ( t ) .

4)

Nếu tồn tại giới hạn x( +0) = lim x( t ) thì x( +0) = lim sX ( s) .

5)

Nếu tồn tại giới hạn lim x( t ) thì lim x( t ) = lim sX ( s) .

t 0

t

s

t

s0

ứng dụng:
1)

Mô tả hệ tuyến tính tham số hằng.

2)

Giải phơng trình vi phân thờng v phơng trình vi phân đạo hm riêng.

3)

Khảo sát đặc tính tần số của tín hiệu causal.

4)

Bảng tra ảnh Laplace một số tín hiệu causal thờng gặp:
x(t)

X(s)

x(t)

(t)

1

1(t)

1
s+a

t

e

at

tn
n!
1
T

1

n +1

t

e T

1
1 + Ts

t

e T

1
s(1 + Ts)

tn
n!T

s +
2

s2
1
s( s + a)

n +1

e



t
T

1
(1 + Ts)n +1
t

1



sin( t)

1
s
1

1 e at
a

1
s

X(s)

2

T ' T T
e
T

1+T 's
s(1 + Ts)
s

cos( t)

s + 2
2

Bi tập:
1)

Xác định ảnh Laplace X(s) cho các tín hiệu causal sau:
a) x(t)=te

2)

22

at

b) x(t)=2+t+3t 2

d) x(t)=tsint

e) x(t)=t 2 sint
Tìm tín hiệu x(t) có ảnh Laplace X(s) sau:
2
1+ s
b) X(s)=
a) X(s)=
(1 + s)(2 + s)
2+s

c) x(t)= (t)e

at

f) x(t)=(t+t 2 )cost
c) X(s)=

1+ s
s(2 + s)2

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội


5.2

Hm truyền mô tả hệ liên tục tuyến tính tham số hằng

Định nghĩa: Xét hệ SISO liên tục, với tín hiệu vo u(t), tín hiệu ra y(t). Hm truyền
đợc hiểu l:
G( s ) =

L { y( t )}
L {u( t )}

=

Y ( s)
, khi trạng thái đầu của hệ bằng 0.
U ( s)

(5.3)

Mô hình:
1)

Với hệ tuyến tính tham số hằng thì hm truyền (5.3) l
một mô hình (hình 5.1):

{

2)

}

y( t ) = L1 {G( s) U ( s)} = L1 G( s) L {u( t )}

G( s) : u( t )
Hm gốc g(t)= L

1

u

y

G(s)

Hình 5.1: Sơ đồ khối

{G(s)} của hm truyền G(s) l hm trọng lợng (xem lại mục

2.1). Nó cũng l mô hình của hệ theo nghĩa tích chập (2.11).
3)

Đáp ứng h(t) của hệ với kích thích 1(t) ở đầu vo đợc gọi l hm quá độ. Hm
quá độ ny cũng l một mô hình của hệ theo nghĩa:
h( t ) : u( t )

y( t ) = h(0)u(0) ( t ) +

d t
h( t )u( )d
dt 0

(5.4)

v có quan hệ với hm truyền nh sau:
G( s )
G( s )
h( t ) = L1 {
H ( s) = L{ h( t )} =

}
s
s
4)

Từ mô hình vora của hệ tuyến tính tham số hằng:
a0 y( t ) + a1

dy( t )
+
dt

+ an

d n y( t )
dt

n

= b0u( t ) + b1

du( t )
+
dt

+ bm

d mu( t )
dt m

ta có hm truyền:
G( s ) =

b0 + b1 s +

+ bm sm

a0 + a1 s +

+ an sn

e s

Hệ y(t)=ku(t ) với hm truyền G(s)=ke
5)

s

đợc gọi l hệ trễ (khâu trễ).

Từ mô hình trạng thái (2.12), (2.13) của hệ liên tục tuyến tính SISO tham số
hằng, ta có hm truyền:
G( s) = C( sI A )1 B + D với I l ma trận đơn vị

6)

Từ hm truyền G(s) ta cũng suy ra đợc hm đặc tính tần: G( j ) = G( s) s = j .

Bi tập:
1)

Hãy xác định hm truyền, hm trọng lợng v hm quá độ của các hệ cho ở hình
1.5. Từ đó xác định đáp ứng của chúng khi tín hiệu vo l u(t)=2sin(t).

2)

Chứng minh rằng ở hệ tuyến tính tham số hằng, hm truyền định nghĩa bởi (5.3)
l không phụ thuộc tín hiệu vo u(t).
dh( t )
Chứng minh quan hệ
+ h( t ) ( t ) = g( t ) v từ đó l công thức (5.4).
dt

3)

Bài giảng môn học Tín hiệu và Hệ thống. Hà Nội 9.2010

23


6

Phép biến đổi Z và hàm truyền hệ không liên tục

6.1

Phép biến đổi Z

Phép biến đổi Z l trờng hợp riêng của phép biến đổi Laplace, áp dụng cho tín hiệu
causal không liên tục {x k }, k=0,1,2,. Sử dụng khái niệm hm mở rộng (1.1), đặc biệt

l hm trích mẫu (1.2), thì dãy vô hạn causal trên sẽ l:
{x k }= x( t ) =



xk ( t kTa )

(6.1)

k=0

trong đó Ta l chu kỳ trích mẫu để có dãy vô hạn {x k }, k=0,1,2, từ tín hiệu causal liên
tục x ( t ) . Thay hm mở rộng (6.1) vo công thức định nghĩa phép biến đổi Laplace (5.1)
ta sẽ có cùng với ký hiệu z = esTa cũng nh điều hiển nhiên rằng x k =0, khi k<0, ảnh
Laplace của dãy vô hạn {x k }, k=0,1,2, nh sau:
X ( s) =





0 k=0

0

=

k=0



st
st
st
x( t )e dt = xk ( t kTa )e dt = xk ( t kTa )e dt


xk e

k=0

ksTa

=



xk z

k

đ.n.

= X ( z)

(6.2)

k=0

Hm X(z) trong (6.2) đợc gọi l ảnh Z của dãy {x k }, k=0,1,2, v phép biến đổi từ dãy
{x k }, k=0,1,2, thnh X(z) đợc gọi l phép biến đổi Z, ký hiệu bởi Z{ }, tức l:
X(z)= Z {x k } v {x k }= Z

1

{X(z)}

Tính chất:
1)

Phép biến đổi Z có đầy đủ các tính chất cơ bản của phép biến đổi Laplace:
a)

Tuyến tính: Z { axk + byk } = aZ { xk } + bZ { yk } , a, b R

b)

Nội xạ: {x k }{y k } Z {x k } Z {y k }

c)

ảnh của tích chập bằng tích của hai ảnh Z { xk i yi } = Z { xk }Z { yk }

k

i=0

2)

Ký hiệu X(z) l ảnh Z của dãy {x k }, k=0,1,2,. Khi đó:
Phép dịch trái: Dãy {y k } với y k =x k m sẽ có ảnh l Y(z)=z

b)

m


Phép dịch phải: Dãy {y k } với y k =x k + m sẽ có Y ( z ) = zm X ( z ) xi z i
i=0



c)

z
Tính đồng dạng: Dãy {y k } với y k =a k x k sẽ có Y ( z ) = X
a

d) Hiệu lùi: Dãy {y k } với y k =x k x k 1 có Y ( z ) =
e)

24

m

a)

X(z)

z 1
X ( z)
z

Hiệu tiến: Dãy {y k } với y k =x k +1 x k có Y(z)=(z1)X(z)zx 0

N.D.Phớc, Bộ môn ĐKTĐ, Trờng ĐKBK Hà Nội