TS. PHẠM ĐỨC PHUNG
BÀ I T Â PT Ậ P
■
■ 4 1 * # 1 ■ ■ ■ « 1
bền vật liệu
■ ■
IBIIHWHHW IIflU H
"■ ia ịiiư ẽíịịịB ^
Ì ÌÌÍ Í B ỊI ỊỊỊ T ^ C
nunHUnW4',!!
menu?.,!'
r n m m m
a
BỊC1SỈ
Ml! BĨ'ft*
w nil BP.:;,!
■ MSBIPĨi
;i
BBS
y 9 ^ - H «»H H It»
¥s$Êễ
Ị Ị’ >1
■>u"«
?}>'>>>>>>>>>>>> h r n iD ỉr n m ri
'W Ề t
NHÀ XUẤT BẢN XÂY DỰNG
TS. PHẠM ĐỨC PHUNG
BÀI TẬP
■
NHÀ XUÁT BÀN XÂY DỰNG
HÀ NỘI - 2008

LỜI NÓI ĐẦU
Trong hệ í hống kiến thức nền tàng của kĩ sư các ngành kĩ thuật xây dựng
công trình, cầu đường, cơ khí, những hiếu biết về các môn cơ học biên
dạng, đặc biệt là môn học Sức bển Vật liệu là kiến thức cơ sờ không thê
thiếu trong, chương trình đào tạo các cún bộ kĩ thuật và những nguyên lí vê
Sức bền Vật liệu được vận dụng trong tất cả các khâu thiết kế đến thi công.
Cuốn bài tập Sức bền Vật liệu này nhằm giúp đỡ cho sinh viên giám bớt
những khó khăn trong quá trình học, đồng thời nam được phương pháp vù
một sổ kĩ năng cần thiết đế giai bài tập sức bền vật liệu.
Trong tài liệu có trình bày khái niệm cơ ban cùa phần lí thuyết, các chỉ
dẫn cần thiết về phương pháp, những thí dụ giải bài toán chọn lọc, các bài
tập tự giải, đáp số, sổ liệu tra cứu hoặc hướng dẫn cách giai.
Tác giả xin chân thành cảm ơn các thầy, cô giáo Bộ môn Sức bền Vật liệu
cơ hục kết cấu trường Đại học Kiến trúc Hà Nội, PGS TS. Lê Ngọc Hồng;
PGS TS. Nguyền Tài Trung và các bạn đồng nghiệp đã tận tình giúp đờ tác
gia hoàn thành cuốn sách này.
Trong quá trình biên soạn cuốn sách chắc chan không tránh khỏi những
khiếm khuyết nhắt định. Tác giá mong nhận được ý kiến đóng góp và phê
bình cua bạn đọc. Mọi ỷ kiến đóng góp xin gưi về: Phòng Biên tập sách
Khoa học Kỳ thuật - Nhà xuất ban Xây dựng - 37 Lê Đại Hành - Hà Nội.
Điện thoại: 04.9741954.
Tác giả
3
NHỬNG ĐƠN VỊ ĐO THƯỜNG GẬP (HỆ ĐON VỊ QUỐC TÉ: SI)
m; cm, mm, kg; s - đơn vị chiều dài, khối lượng, then gian (là những đơn vị cơ bản),
mét, cent’ẵmét, milimét, kilôaam, giây.
N - đơn vị là Niutơn: IN = l/9,81kG.
kN; MN; DaN - đơn vị bội số lực - kilôniutơn, Mêga Niutơn, Đeca Niu tơn:
lkN = 103N; 1MN= 106N; ldaN= 10N.

N/m2; MN/m2 - đơn vị ứng suất và áp suất. MN/m2 = 103 kN/m;
lkN/m2 = 103 N/m2;
HỆ ĐON VỊ Kĩ THUẶT (MKS):
m; kG; s - mét; kilôgam lực; giây: 1 kG = 9,8IN;
T - tấn - lực: 1 T = 103 kG;
kG/cnr - đon vị đo ứng suất và áp suất: 1 kG/cm2 = 9,81.i04 N/rn2
kMm - đon vị công: 1 kMm = 9,81 jun.
1 mã lực = 75 kGm/s.
ĐƠN VỊ ĐO LƯỜNG QUỐC TÊ VỀ CÁC ĐẠI LƯỢNG c ơ HOC
TT
Tên đại lượng Tên đơn vị Ký hiệu Quan hệ các đơn vị
1 Lực
Niutơn N IN = 0.1 kG
2
Lực phân bố
N/m lN/m = 0.1 kG/m = 10' 3 kG/m
3
úns suất
Pascal
Pa
lPa = 0,lkG/m: = 10'4T/nr
4 Mô đun đàn hồi
Pascal
Pa
lPa = 10'4 T/m
5
Cường độ tải trọng
Pascal
Pa
lPa = 10 kG/cm: = 10: T/nr

6
Phàn bố bể mặt
lkPa = 0,1 T/rrr
7
Mỏ men lực
Nm
lNm = 0,1 kGm = lOkGm
8
Khối krone
kg
5
BẢNG CÁC KÝ HIỆU VÀ CHỮ VIẾT TẮT
ụ. - Hệ sô Poisson
ơ - Úng suất pháp.
T - Úng suất tiếp.
(0 - Tần số dao động riêng.
(p - Góc xoay trong mặt phẳng xoy.
A - Chuyến vị theo phương thẳng đứng.
5 - Chuyển vị nhỏ theo phương thẳng đứng.
Q - Tần sô dao động cúa lực kích thích.
E - Mô đun đàn hồi cùa vật liệu,
p - Lực tập trung.
M - Mô men tập trung,
q - Tái trọng phân bồ đều theo chiều dài.
Nz - Lực dọc theo phương của trục z.
Qy - Lực cắt theo phương trục Y.
Qx - Lực cắt theo phương trục X.
Mx - Mỏ men uốn xung quanh trục X.
My - Mò men uốn xung quanh trục Y.
My - Mô men xoắn xung quanh trục z.

[ơ] - úiig suất pháp cho phép .
Kd - Hệ số K động cho va chạm.
T - Chu kỳ dao động.
J - Mỏ men quán tính.
[f ] - Độ võng cho phép.
Chuong I
LÝ THUYẾT NỘI VÀ NGOẠI Lực
I. CÁC CÔNG THỨC CẨN THIẾT
- Sư dụng phươnc pháp mặt cắt để vẽ biểu đồ nội lực. Đôi với bài toán phăng có ba
thành phần nội lực: Nz, Qy và Mx.
- Quy ước dấu cho các nội lực (hình 1-1).
Qy>0
M>0
0 ^
M„>0
-► N >0 Nz>0
c
Qy>0
r ^ P ,
Hình 1-1
+ Lực dọc N, > 0 khi hướng ra ngoài mặt cắt và gọi là lực kéo; ngược lại là lực nén.
+ Lực cắt ọ > 0 khi pháp tuyến ngoài của mặt cắt, quay thuận chiều kim đông hô
một góc 90 ° thì trùng với chiều lực cắt Qv
+ Mômen uốn Mx > 0 khi nó làm căng thớ dưới hay nói một cách khác mômen làm
căng các thớ về phía dươna cua trục oy.
- Liên hệ vi phân giữa tải trọng phân bố q với lực cat Qv và mômen uốn Mx:
dQv
dMx
dz
= Q y ;

d2M,
= q
(
1
-
1
)
dz dz dz"
- Biêu đồ nội lực là đồ thị biểu diễn các thành phần nội lực theo hoành độ z. Từ biểu
đồ nội lực xác định được giá trị nội lực lớn nhất đó chính là mặt cat ne uy hiêm.
- Trên sơ đồ chịu lực chịu tải trọng q = const thì biểu đổ lực cắt ọ > là bậc nhất và biếu
đổ mô men uốn Mx là đường bậc hai.
- Nếu trên biểu đổ lực cát QN = 0 thì trên biểu đồ mô men uốn Mv đạt cực trị.
- Tai mặt có lực tập trung p hoặc mô men tập trung M thì trên biếu đồ lực cắt Qy mỏ
men uốn Mv có bước nháy đung băng giá lực tập trung hoãc mô men tập truns.
7
II. BÀI TẬP CHỌN LỌC
Ví dụ 1-1
Cho dầm chịu lực (hình 1-2): P] = P2 = 20 kN;qi = lOkN/m; q2 = 12kN/m;
q3 = 2kN/m;; Mi = 12 kNm; M2 = 15 kNm; a= lm. Vẽ biểu đồ lực cắt Qy và mômen
uốn Mv.
Hình 1-2
I
Giải:
a) Xác định phán lực Rạ = ? RB = ?
]Tm A = 0 -» RB = 34kN
J m B=0 -> Ra - 40 kN
Kiêm tra phản lực xác-định có đún» không;?
=40 + 3 4 - 10x2- 12x1 - 2x 1 -2x20 = 0
Điêu đó chứng tỏ, xác định phán lực là đúng.

b) Vẽ biêu đô lực cat Qy và mômen uốn Mx
- Áp dụng phương pháp mặt cắt.
- Chọn gốc tọa độ ớ o.
- Đoạn OA. Xét sự cân bằng phần trái, với điều kiện 0 < Zị < lm
Tổng mômen với trọng tâm mặt cắt 1-1:
n 7 2
£ m M = M x+ M 2- ^ L = 0
Q
8
Mx = 5zf —15
Tổng hình chiếu lên trục Oy:
X y = Qy+iO z,=o _► Qy = -I0z
Đường biếu diễn lực cắt Qy là bậc một, mômen uốn Mx là đường bậc hai thể hiện trên
hình 1-1 a.
- Đoạn AC với điều kiện lm < z2 <2n
bàng phân bên trái:
Zy = Qy2 + 10z2 - RA =0
Qy2= 4 0 -1 0 z 2
Tống mômen với trọng tâm mặt cắt 2-2:
Mx =40(z2 - l ) -5 z ị -15
- Đoạn CD với điều kiện 2m < z3 <3m
Xét cân bằng phần trái
£ y = Qy3 +10x2 + 12(z3-2 ) -4 0 = 0
Qy4 = -20 - 12(z3 - 2) + 40
= 2 0 - 12(z3-2)
M,
X m3-3 = Mn3 + M 2 + 12
91
c
Ra

■20(z3 -1) = 0 Mx4 J
Mx3 = 20(z3 — 1) —15 - 6(z3 - 2)
- Doạn BK với 5m < z4 < 6m. Xét cân bàng phần
bên phải.
Ọy4 = 20
M,4 = - 20(6 - z4)
- Đoạn HB với 4 m < z5 <5in. Xét cân bàng
phần bên phai.
Qy5 = 20 - 3 4 = -14
Mõ = -20(6-zs) + 34(5-z5)
M.
Q2
M,
y3
6 -Z,
6 - l i
9
M,
*6 JT Q3
M,
B
- Đoạn DH với 3m < z6 < 4m . Xét sự cân
bang phần phải.
I y = Qy6 + RB-P 2 - 2(4 - z 6) = 0
Qyó = - 1 4 + 2 ( 4 - Zó)
Mx6 = - 20 (6-z 6) + 34(5 - z6) + 12 - (4-zó)2
Biếu đồ lực cắt Qy và mômen uốn Mx thể hiện
trên hình 1-2
Ví dụ 1-2. Một dầm chịu tải trọng như hình 1-3. Cho M| = 2Tm; M2 = 12Tm;
qi=2T/m; q2 = 4T/m; p = 12T. Vẽ biểu đồ lực cắt Qy và mômen uốn Mx.

/77777^77
R«
6-Zg
-> Ra = 2T
-> Rb = 6T
Hình 1-3
Giải:
1) Xác định phản lực.
Z m B = 0
Z mA = 0
Kiểm tra phan lực xác định có đúrm khôno,.
£ y = RA+ R B+ 1 2 -2 x 2 -4 x 4 = 0
2) Vẽ biêu đồ lực cắt Qy và mômen uốn Mx.
- Đoạn AC với 0 < Z| < 3m . Xét cân bans phần trái.
Q yi = R a = 2
lơ
Z mi-| = M xI - 2 - 2 ỂZ| =0
MX1 = 2Z| + 2
- Đoạn CD với 3m < Z| < 5m . Xét cân băng phân trái
5]y = 0 -> Qy2 = 2 - 2(z2 - 2) M,
Q>2 = 0 —> Z2 = 4 m
Q>2 = U —> Z2 = 4 m
= MX7- M |-2.Z-, +2.—-— — = 0 ,»2^
^ z / 2 _ n
") Ra •—
Mx2 =2z2 + 2 - ( z 2 -3)'
z2 =3m —> Mx2 = 8Tm
Zt = 5m —> Mx2 = 8Tm
z2 = 4m -> Mmax = 9Tm
Đoạn EB với 6m < Z 3 < lOm. Xét cân bàng phần phải

Xy = 0 —> Qy3 = 4(10 - Z3) - 6
z3 = 6m -> Ọy3 = 10
z =10mm —> QV1 = —6
Q,3 = 0 z, = 8,5m
3 q2
_ A
10-Z3
V- (10 —Z )2
^ m ._ .= M l - M x3 H-4^ ^ + 6 .(1 0 - z3) = 0
M,3 = 2 - 2 (]0 -z 3)2 + 6 (I0 -z 3)
z3 = 6 Mx3 = -6
z3 =10 —» Mx3 = 2
z3 = 8,5 ^ Mmax =6,5
- Đoạn DE với 5m < z4 < 6m . Xét cân bàna phần phải
Q> = - 2 M,
M \4 = 2 + 6(10 - Z4) + 12 (6 - Z4) - 16(8 - Z4)
- Nhận xét:
. Q
Tái trọng phàn bò q = const thì biêu đô lực căt
Qy là đườns bậc nhất, mômen uốn Mx là đươim
bậc 2 (thi dụ đoạn CD. đoạn EB)
Q1
M,
1 5
Rb
q2
10 - z4
/777ZV7/////
Tại mặt cắt Qy = 0 thì mômen đạt cực đại. Mxmax = 9 (Tm), Mmax = 6,5 (Tm).
Tại mặt cắt có lực tập trung (Tại E) thì trên biểu đồ lực cắt Qy có bước nhảy đúng

bàng giá trị lực tập trung.
Tại mặt cắt có mômen tập trung (tại A, B, D) thì trên biểu đồ mômen có bước nhảy
lực tập trung đúng bằng giá trị mômen tập trung.
Ví dụ 1-3: Cho 1 dầm đặt trên hai gối tựa A và B. Chịu tải trọng như hình 1-4.
q = lOkN/m; p = 2kN; Ml = 2kNm; a = l,5m; b = lm; M2 = 4kNm; M3 = lOkNm. Vẽ
biểu đồ Qy và Mx.
Giải:
a) Xác định phản lực
mA = 0 —» Rb = 3kN
^ m B = 0 -> R A = 29kN
Kiểm tra:
5 > = RA + Rb -1 0 x 3 - 2 = 0
Điều đó chứng tỏ xác định phản
lực là đúng.
b) Vẽ biểu đồ Qy và Mx
Áp dụng phương pháp mặt cắt.
Bài này chia làm 4 đoạn.
Chọn hệ trục yoz
- Đoạn OA. Tướng tượng mặt cắt
1-1 cách gốc tọa độ o một khoảng
Z\ với 0 < Zị < l,5m. Xét cân bằng phần trái.
Qyl = -10.Z,
2 > , _ , = M xi + M 2 + q y = 0
MX| = -4 - 5 z f
- Đoạn AC. Mặt căt 2-2 với l,5m < z2 < 3m . Xét cân bằng phần trái.
Qy2 = 2 9 - 10.Z2
Qy2 = 0 thì z2 = 2,9m
z 2
^ m 2_2 = M x2 + M2 + ( \ ~ ~ Ra (z2 -1,5) = 0
"3 ra

12
Mx2 = -4 -5 z |+ 2 9 (z 2 -1,5)
z2 = 1,5m -> Mx2 =-15,3 kNm
z2 = 3m -» Mx2 = -5,5 kNm
z2 = 2,9m -> Mmax = -5,45 kNm
/7707?
^2
7&P
Ra
M.
- Đoạn DB mặt cat 3-3 với 4,5m < z3 < 5,5m xét cân bàng phần phải.
Qy3 = - R b = - 3 M
X m3-3 = Mx3 + M 3 - 3(5,5- z 3) = 0
Mx3 = -10 + 3(5,5 - z 3)
- Đoạn CD ta có thể suy ra tại mặt cat DC
+ Lực cắt có bước nhảy p = 2kN
+ Mômen uốn có bước nhảy Mi = 2kNm ( hình 1-4)
Biêu đồ lực cat Qy và mômen uốn Mx thể hiện trên hình 1-4.
Ví dụ 1-4: Cho dầm AB chịu lực như hình 1-5. Vẽ biếu đồ Qy và Mx.
’rQ
ơ/ẳ<//ệ;
- Tìm phan lực: R\ - 15kN; Rb = 3kN
- Áp dụng phươnu pháp mặt cát vẽ biêu đồ và biểu đồ Mv Trên hình 1-5.
13
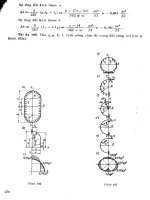
Ví dụ 1-5. Cho thanh cong 1/4 đường tròn, bán kính R. Chịu tải trọng phân bố đều q.
có chiều hướng vào tâm o (hình 1 - 6) Hãy vẽ biểu đồ Qy Mx Nz
Hình 1-6
Giải:
- Thực hiện mặt cắt 1-1 qua tâm o tạo với phương thăng đứng OB một góc (p hình l-6e.
- Họp lực tài trọng phân bố trên đoạn BC có phương hướng vào tâm o là

p = 2qRsin —.
2
]Tz = Nz + 2qRsin—.sin — = 0
Nz = -2qRsin2 — = -qR(cos(p - 1)
= Qy -2qRsin —.COS—= 0
Qv = qR sincp
^m|_] = Mx -2qRsin — .Rsin— = 0
Mx = qR2(l -coscp)
14
Lập bảng biến thiên:
\ (p
Nội lực\.
0 30°
45°
60°
vo
o
o
Nz 0
q R ( V Ỉ - 2 )
2
qR( 7 ĩ - 2>
2
+qR
2
qR
Qy
0
qR
2

qR
Mx
0
qR^ 2 - ^
2
2
2
qR2
Biếu đồ lực dọc Nz, lực cắt Qy và mômen uốn Mx thể hiện trên hình 1-6.
Ví dụ 1-6. Cho thanh cong một nứa hình tròn, đường kính d = 2R chịu lực tập trung
p = qR và M = qR: (hình 1-7). Hãy vẽ biểu đồ lực dọc Nz, lực cắt Qy và mômen uốn Mx.
0,86-q.R
Hình 1. 7
15
Giải:
a) Quy ước dấu:
- Lực dọc Nz > 0 khi có hướng ra ngoài và luôn tiếp tuyến với đường cong.
- Lực cắt Qy > 0 khi pháp tuyến ngoài của mặt cắt quay thuận chiều kim đông hô mọt
góc 90° thì cùng chiều với lực cắt Qy (giống thanh thẳng).
- Mômen uốn Mx > 0 khi làm thanh cong thêm. Đối số được chọn là góc ọ .
b) Vẽ biểu đồ lực dọc Nz, lực cắt Qy, mô men uốn Mx.
Áp dụng phương pháp mặt cắt:
* Xét đoạn AB: Tưởng tượng có mặt căt 1-1 đi qua tâm o tạo với phương năm ngang
góc (p , xét sự cân bằng phần bên dưới (hình l-7f):
- Mặt cắt 1-1: 0 < Ọ) <71/2. Biểu diễn các thành phần nội lực trên mặt cắt:
+ Lực dọc Nz theo phương tiếp tuyến với thanh cong tại điểm cắt, cũng là phương
trục OZ, phương trục OZ luôn biến đổi theo đường cong của thanh.
+ Lực cất Qy vuông góc với trục OZ tại mặt cắt (biểu diễn theo chiều dương).
+ Mô men uốn Mx luôn biểu diễn theo chiều dương (làm thanh cong thêm).
+ Từ trọng tâm mặt cắt ta hạ đường h _L OA .

= Nz -Psincpj = 0 => Nz = q.R.sin (P|
X y = Qy + P-COScp, = 0 = > Qy =-q.R.C0S(p,
^ n i|_ | = Mx - M + P.h = 0=> M x =qR 2 -q.R 2Ểsin(p!
=> M x = q .R 2.(l — sin(Pj)
- Lập báng biến thiên:
Nội lực
0
n /6 tc/4
7t / 3
71 / 2
Nz
0
0,5.q.R
0,7.q.R
0,86.q.R
q.R
Qy
-q.R
-0,86.q.R
-0,7.q.R
-0,5.q.R
0
Mx q.R2
0,5.q.R2
0,3.q.R2
0,13.q.R2
0
- Vẽ biểu đồ nội lực tại các điểm đặc biệt theo góc (Pi.
* Xét đoạn CB:
- Mặt cắt 0 < (p2 ^ tc/2

- Biểu diễn các thành phần nội lực trên mặt cất 2-2 ( hình l-7e):
£ z = N z + R c .cos(p2 - H c .sin(p2 = 0 => N z = q.R.sincp2 -q.R.C 0S(p2
=> N z = q.R.(sincp2 -cos(p2)
16
^ y = Qy - Rc sin ọ 2 + Hc COS(p2 = 0 => Qy - qR sin <P2 + cos^2
=> Qy = qR(sin(p2 +C0S(p2).
X m2-2 = Mx - Mc + Hch2 + RC(R - R cos(p2) = 0
=> M x = 2qR2 -q R 2 sincp2 ~qR2(l-C 0 S (p 2)
- Lập bảng biến thiên:
Nội lự c'\^
0 7t/6
71 / 4
n /3
n /2
Nz
-qR
-0,36qR
0 0,36qR qR
Qy
qR
l,36qR
l,4qR
l,36qR
qR
Mx 2qR2
l,36qR2
qR2 0,63qR2 0
Vẽ biêu đô nội lực Nz; Qy và mômen uốn Mx theo góc (p2 thê’ hiện trên hình 1-7
Vi dụ 1-7. Cho một khung phắng ABCDE chịu tải trọng phân bố đều q, lực tập trung
p và mô men tập trung M như hình 1-8. Vẽ biểu đồ lực dọc Nz, lực cắt Qy và mô men

uốn Mx.
a)
2qa

b)
a
M=qa‘
2a
©
X2)
3qa
2qa
c)
2qa
3qa
3qa
qa
Hình 1.8a, b, c, d
17
Giải:
a) Xác định phản lực
X Ma =0=> R b =3qa
£ x = 0 =}Ha = qa
£m b =0=>RA =2qa
b) Xét đoạn AE
Tưởng tượng mặt cắt 1-1 cách gốc tọa độ a một khoảng
Z\. Với điều kiện 0<Zị < a . Xét sự cân bằng của phần
dưới (Đối với khung trục z bao giờ cũng chọn theo trục của
thanh). Hệ trục tọa độ chọn như hình l-8e
Z z = 0

Z, = 0
=> Nzl = -zqa
£ y = 0 ^ Q yl= -qa với =a
=0 ^ M xl = qa.Zj
M,
0
Mxl =qa^
c) Xét đoạn EC
Ta tưởng tượng mặt cắt 2-2 với điều kiện a < z 2 <2a.
Xét sự cân bàng của phần dưới hình l-8f.
Z z = 0
N
7 . 2
£ y = 0 =?Vy2 = - j qa
' ^ ]M 2_2 = 0 => Mx2 = - q a - 2 - 2 q a ( z -a )
- 2qa
Qv2 = -3qa
với
z = a
z = 2a
Mx2 = -qa 2
Mx2 =-4qa^
d) Xét đoạn BD.
Tướng tượng mặt cắt 3-3 cách gốc tọa độ B một khoảng
z3 với 0 < z3 < a . Chọn gốc tọa độ ở B. Xét sự cân bàng
của phân dưới hình 1 -8g.
E z = 0 =>Nz3=0
X y =0 =>Qy3= 3 qa
Z M3-3 = ° =>M x3 = qa2 -3qa.z
với

I z = 0
z = a
Mx3 =qa
Mx3 =2qa2
Hình l-8f
18
e) Xét đoạn CD.
Tưởng tượng mặt cắt 4-4 cách gốc tọa độ D một khoảng Z4 với điều kiện 0 < z4 < 2a
Xét sự cân bàng của phần phải hình l-8h. _
Z z = 0 =>Nz4 =-3qa
]T y = 0 ^>Qy4 = q z
z 2
£ M 4_4 =0 = >M x2 = qa2 -3 qa2 -q .± -
với <
z = 0 M
x4
-2 qaz
,-y
z = 20 => M x4 = -4qa
z = a =>M x4 =-2,5qa
Biểu đồ Nz, Qy và Mx vẽ trên hình 1-5 a, b, c
Chủ ỷ: Đối với khung cần kiểm tra sự cân
bàng tại nút. c và D thể hiện trên hình l-8i.
4qa2
3qa
3qa
2qa
2qa
3qa
2qa

Hình 1-8L
III. BÀI TẬP
1-1. Vẽ biểu đồ Qy và Mx của dầm chịu lực như hình 1-9.
í t
M
§ hb
Hình l-8h
3qa / / / * / / / /
2qa
/ / 7 / 7 /,
'////
/
/ 77 777 /
Hình 1-9
19
1-2. Không cần tính phản lực, vẽ biểu đồ nội lực của các dầm cho trên hình 1-10.
Hình 1.10
1-3. Biếu đồ Ọy và Mxcho dầm chịu lực đơn giản thể hiện ở bảng 1.
Bảng 1
STT
Sơ đồ
Biổu đồ Qy
Biểu đồ Mx
©
q
/
q'r g n - T - r - '
q/2/2
II2
Ị

P/2U
J D P /2
P//4
q//2[ r ^
^q^Ịq//2
3 -
Mmax=q/2/8
q//6
©
2
q/
M—■ 973
^ U Ì U Ì L U ^
1-4.
Cho một dầm chịu tải trọng q. p. M như hình 1-11. Vẽ biểu đồ lực cat Q, và mô
men uốn Mx
20
21
Hình 1-11 (tiếp theo)
1-5. Vẽ biểu đồ lực cất Qy và mô men uốn Mx của dầm chịu lực như hình vẽ 1-12.
q=2T/m
4T.m
4T m
-*ị.
I = 2m -Ỵ-
b)
2q
A
q
TÌTT

jzazt&77zy
Ạ I 1
3/
M0=q/2
q
/
s ị i , 1 p*2q' 2/ «Ặ,
d) .2
' q/ /4
%
q/2/4
r c K t t g
I /77ỹ7hffflF
^ q/2 q 2q/2 2q/2 q/2
—V-
2
/
2/
9J
T T
í 1 ị
/ 1
/

1
1
ĩ ^ | , ^ ím4 r J
L A ,
2m
////ệ/z 7-72

"79
1-6. Vẽ biểu đồ nội lực của thanh cong chịu lực như hình vẽ 1-13.
a)
q=10kN/m
b)
Hình 1-13
1-7. Cho dầm chịu lực như hình vẽ 1- 14. Cho q, = 8kN/m;
q2 = 16kN/m; p = 12kN; M = 12kNm; a = 2m.
- Vẽ biểu đồ Qy và Mx
Đớp án:
- Xác định phán lực: RA = 2kN;
Rb = 86kN
- Vẽ biểu đồ Q và Mx hình 1-14.
Hình 1-14
23
l-8ế Một dầm chịu lực như hình 1-15a, b.
Vẽ biểu đồ lục cất Qy và Mx.
a) Cho q = 12kN/m; p = 30kN;
M = 12kN; a = 2m.
Vẽ biếu đồ Qy và Mx?
Đáp án:
- Xác định phản lực: RA = 30kN;
Rb = 48kN.
- Vẽ biểu dổ Q và Mv hình 1-15a
b) Cho q = lOkN/m; p = 20kN; M = 20kN; a = lm
Vẽ biểu đồ Qv và Mxl'
Đáp án:
- Xác tiịnli phán lực: RA = 20kN;
Rb = 40kN.
- Vẽ biếu đồ Ọ> và hình 1.15b

24
©
1-9. Sử dụng tính chất
đối xứng đê vẽ biếu đồ lực
dọc Nỵ; lực cắt ọ ; mô men
uốn Mx của khung chịu lực
như hình l-16a, b, c, d.
a) Cho q = 2kN/m;
p = 2kN;
M = 2kNm; a =2m;
Vẽ biểu đồ Qy và Mx?
Đáp án:
- Xác định phán lực:
RB = 2kN;
Mb = 2kN
- Biểu đổ Q_n và Mx hình
1 -16a.
b) Cho qi = 2kN/m;
C]2 = 4kN/m;
P = 4 k N ;a = lm;
Vẽ biếu đồ Qy và Mx?
Đáp án :
- Xác định phán lực:
Ra = 13/4 kN;
Rb = 27/4 kN.
q = 2kN/m.
p = 2kN
M„= 2kNm
Hình 1-16(1
MB = 2