Ngày soạn:
Ngày dạy:
Tiết 61

HÌNH NÓN - HÌNH NÓN CỤT - DIỆN TÍCH
XUNG QUANH VÀ THỂ TÍCH CẦU CỦA HÌNH NÓN,
HÌNH NÓN CỤT
A. MỤC TIÊU:
- Kiến thức: HS được giới thiệu và ghi nhớ các khái niệm về hình nón: đáy, mặt xung
quanh, đường sinh, đường cao, mặt cắt song song với đáy cảu hình nón và có khái
niệm về hình nón cụt.
- Kĩ năng : Nắm chắc và biết sử dụng công thức tính diện tích xung quanh, diện tích
toàn phần và thể tích của hình nón, hình nón cụt.
- Thái độ : Rèn luyện tính cẩn thận cho HS.
B. CHUẨN BỊ:
- GV: Mô hình hình nón, thiết bị quaytamgiacs vuông ABC tạo thành hình nón, tranh
vẽ H87,92,93,94 nón cụt
- HS: dụng cụ học tập

C. TIẾN TRÌNH DẠY HỌC

1. Tổ chức:
1. Tổ chức: 9A
9B
9C
2. Kiểm tra:
Giáo viên giới thiệu bài học
3. Bài mới
Hoạt động của Thầy Hoạt động của học sinh
1. HÌNH NÓN
- GV giới thiệu: quay ∆ vuông ⇒ hình nón.

Khi quay:
+ Cạnh OC quét nên đáy của hình nón, là
một hình tròn tâm O.
+ Cạnh AC quét nên mặt xung quanh của
hình nón. (AC: đường sinh).
A: đỉnh.
AO: đường cao.
- GV đưa hình 87 SGK để HS quan sát.
HS nghe GV trình bày và quan sát thực
tế, hình vẽ.
?1. Một HS lên chỉ rõ các yếu tố của
hình nón: đỉnh, đường tròn đáy, đường
sinh, mặt xung quanh, mặt đáy.
Hoạt động của Thầy Hoạt động của học sinh
- Đưa nón để HS quan sát và
- Yêu cầu HS làm ?1.
2. DIỆN TÍCH XUNG QUANH HÌNH NÓN
- GV cắt mặt xung quanh của một hình nón
dọc một đường sinh và trải ra.
- Hình khai triển mặt xung quanh của một
hình nón là hình gì ?
- Nêu công thức tính diện tích hình quạt
tròn S
AA'A
.
- Độ dài cung AA'A tính thế nào ?
- Tính diện tích quạt tròn S
AA'A
.
⇒ chính là Sxq của hình nón.

Sxq = π r l
r: bán kính đáy.
l: độ dài đường sinh.
- Tính Stp như thế nào ?
- Sxq của h/c đều ?
Ví dụ: h = 16 cm
r = 12 cm
Sxq = ?
- Hình quạt tròn.
Học sinh Sq = …….
Độ dài cung AA'A chính là độ dài
đường tròn (O; r) ⇒ bằng 2π r.
S
xq
=
=
2
2 rl
π
π r l.
S
xq
= π r l.
Stp = Sxq + Sđ.
= π r l + π r
2
.
S
tp
= π r l + π r

2
Sxq hc đều = P. d.
P: nửa chu vi.
d: trung đoạn.
VD: Độ dài đường sinh của hình nón
là:
Hoạt động của Thầy Hoạt động của học sinh
L =
2222
1216 +=+ rh
= 20
(cm).
Sxq của hình nón:
Sxq = π r l = π. 12. 20 = 240π (cm
2
).
3. THỂ TÍCH HÌNH NÓN
- GV nêu cách xác định công thức tính thể
tích hình nón bằng thực nghiệm như SGK.
- Qua thực nghiệm thấy:
V
nón
=
3
1
V
trụ
.
Hay V
nón

=
3
1
π r
2
. h
Áp dụng: Tính thể tích của 1 hình nón có
bán kính đáy = 5 cm ; chiều cao 10 cm.
Tóm tắt:
r = 5 cm
h = 10 cm
V = ?
V =
3
1
π r
2
h =
3
1
π. 5
2
. 10
V =
π
3
250
(cm
3
).

4. HÌNH NÓN CỤT - DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH HÌNH NÓN
CỤT
a) Khái niệm hình nón cụt:
GV giới thiệu bằng mô hình.

- Hình nón cụt có mấy đáy ?
b) Diện tích xung quanh và thể tích hình
nón cụt:
GV đưa H92 lên bảng phụ giới thiệu: các
- Có hai đáy là hai hình tròn không
bằng nhau.
Sxq của nón cụt là hiệu Sxq hình nón
lớn và hình nón nhỏ.
Hoạt động của Thầy Hoạt động của học sinh
bán kính đáy, độ dài đường sinh, chiều cao
của nón cụt.

- Tính Sxq của nón cụt như thế nào ?
Sxq nón cụt = π (r
1
+ r
2
) l
Tương tự:
Vnón cụt =
3
1
π h (r
1
2

+ r
1
. r
2
).
4. Củng cố.
Hoạt động của Thầy Hoạt động của học sinh
GV củng cố lại các kiến thức đã học và
chốt các công thức cho học sinh.
êl nmen
5. HDVN. `
- Nắm vững khái niệm hình nón.
- Nắm chắc các công thức tính Sxq, Stp, thể tích của hình nón.
- Làm bài tập: 17, 19, 20, 21, 22 <118 SGK>.
Ngày soạn:
Ngày dạy:
Tiết 62

LUYỆN TẬP
A. MỤC TIÊU:
- Kiến thức: Thông qua bài tập HS hiểu kĩ hơn các khái niệm về hình nón. Cung cấp
cho HS một số kiến thức thực tế về hình nón.
- Kĩ năng : HS được luyện kĩ năng phân tích đề bài, áp dụng các công thức tính diện
tích xung quanh, diện tích toàn phần, thể tích của hình nón cùng các công thức suy
diễn của nó.
- Thái độ : Rèn luyện tính cẩn thận cho HS.
B. CHUẨN BỊ:
- GV : Bảng phụ
- HS : Dụng cụ học tập


C. TIẾN TRÌNH DẠY HỌC

1. Tổ chức: 9A
9B
9C
2. Kiểm tra bài cũ:
Hoạt động của Thầy Hoạt động của học sinh
HS1: Chữa bài tập 20 <118 SGK>.
(bảng phụ).
HS2: Bài 21/tr118sgk
- GV nhận xét, cho điểm 2 HS.
HS1: Điền bảng.
Giải thích: l =
22
rh +
. V =
3
1
π r
2
.h.
HS2:
Bán kính đáy của hình nón là:
π r l = π. 7,5 . 30 = 225 π (cm
2
).
Diện tích hình vành khăn là:
π R
2
- π r

2
= π (17,5
2
- 7,5
2
)
= π. 10. 25 = 250π (cm
2
).
Diện tích vải cần để làm mũ (không kể
riềm, mép, phần thừa) là:
225π + 250π = 475π (cm
2
).
3. Bài mới
Hoạt động của Thầy Hoạt động của học sinh
Luyện tập
* Dạng tự luận:

Bài 17 <117 SGK>.
l =
0
0
180
na
π
(1)
- Trong ∆ vuông OAC có: CAO = 30
0
,

Hoạt động của Thầy Hoạt động của học sinh
- Tính số đo cung n
0
của hình mặt xung
quanh của hình nón.
- Nêu công thức tính độ dài cung tròn n
0
,
bán kính bằng a.
- Độ dài cung hình quạt chính là độ dài
đường tròn đáy hình nốn C = 2π r.
Hãy tính bán kjính đáy hinhd nón biết
CAO = 30
0
và đường sinh AC = a.
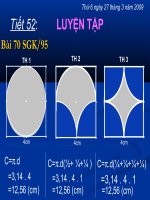
Bài 23 <119 SGK>.
Gọi bán kính đáy của hính nón là r, độ
dài đường sinh là l.
Bài 27.
- GV đưa đầu bài và hình vẽ lên bảng phụ.
- Dụng cụ này gồm những hình gì ?
AC = a ⇒ r =
2
a
.
Vậy độ dài đường tròn (O;
2
a
) là:
2π r = 2 π .

2
a
= π a.
Thay l = πa vào (1): πa =
0
0
180
na
π
⇒ n =
180
0
.
Bài 23:
Để tính được α cần tìm được tỉ số
l
r
hay
tính được sinα.
Diện tích quạt tròn khai triển đồng thời
là diện tích xung quanh của hình nón là:
Sq =
4
2
l
π
= Sxq nón.
Sxq nón = π r l
⇒
4

2
l
π
= π r l ⇔
4
l
= r.
l
r
=
4
1
= 0,25.
Vậy sinα = 0,25 ⇒ α = 14
0
28'.
Bài 27:
HS: Gồm hình trụ ghép với một hình
nón.
Thể tích của hình trụ là:
V
trụ
= π r
2
. h
1
= π. 0,7
2
. 0,7
= 0,343π (m

3
).
Thể tích của hình nón là:
V
nón
=
3
1
π r
2
. h
2
=
π
3
1
. 0,7
2
. 0,9
Hot ng ca Thy Hot ng ca hc sinh

- Tớnh th tớch ca dng c.
- Tớnh din tớch mt ngoi ca dng c.
= 0,147 (m
3
).
Th tớch ca dng c ny l:
V = Vtr + Vnún = 0,343 + 0,147
= 0,49 = 1,54 (m
3

).
Din tớch xung quanh ca hỡnh tr l:
2 r h
1
= 2. 0,7 . 0,7 = 0,98 (m
2
).
Din tớch xung quanh ca hỡnh nún l:
l =
2222
9,07,0 +=+ hr
= 1,14 (m).
Sxq = r l = . 0,7. 1,14 = 0,80 (m
2
).
Din tớch mt ngoi ca dng c l:
0,98 + 0,80 = 1,78 = 5,59 (m
2
).
4. Cng c.
Hot ng ca Thy Hot ng ca hc sinh
Giỏo viờn cng c li ni dung luyn tp
v cỏc cụng thc vn dng
5. HDVN. `
- Nm chc cỏc cụng thc tớnh dtxq v th tớch ca hỡnh nún.
- Lm bi tp 24, 26, 29 <119>.
__________________________________________________
Son:
Ging:
Tit 63



Hình cầu Diện tích mặt cầu và thể tích hình cầu
A. MC TIấU:
- Kin thc: HS nm vng cỏc khỏi nim ca hỡnh cu: Tõm, bỏn kớnh, ng kớnh,
ng trũn ln, mt cu. HS hiu c mt ct ca hỡnh cu bi mt mt phng luụn l
1 hỡnh trũn. Nm vng cụng thc tớnh din tớch mt cu. HS c gii thiu v v trớ
ca mt im trờn mt cu - To a lớ.
- K nng : Thy c ng dng thc t ca hỡnh cu.
- Thỏi : Rốn luyn tớnh cn thn cho HS.
B. CHUN B:
- GV:
Mô hình hình cầu, thiết bị quay nửa hình tròn tâm o, tranh vẽ H103,104,105,112
- HS: Dng c hc tp

C. TIN TRèNH DY HC

1. Tổ chức: 9A
9B
9C
2. Kiểm tra bài cũ: Kết hợp trong bài học
3. Bài mới
Hoạt động của Thầy Hoạt động của học sinh
1. HÌNH CẦU
- Khi quay 1 hình chữ nhật vòng quanh
một cạnh cố định được hình gì ?
Tương tự quay 1 tam giác vuông ?
- Khi quay một nửa hình tròn tâm O, bán
kính R 1 vòng quanh đường kính AB cố
định được hình cầu (GV nói và thực hành).

- Nửa đường tròn trong phép quay tạo nên
mặt cầu.
Điểm O gọi là tâm, R là bán kính của
hình cầu hay mặt cầu.
- GV đưa hình 103 <121 SGK> để HS
quan sát.

- Yêu cầu HS lấy VD.
- Hình trụ.
- Hình nón.
- HS nghe và quan sát GV thực hiện.
2. CẮT HÌNH CẦU BỞI MỘT MẶT PHẲNG
- Khi cắt hình cầu bởi 1 mặt phẳng thì mặt
cắt là hình gì ?
- GV yêu cầu HS thực hiện ?1 <121>.
- GV đưa hình 105 SGK lên giới thiệu với

HS: Trái đất được xem như 1 hình cầu,
xích đạo là 1 đường tròn lớn.
- Mặt cầu là 1 hình tròn.
- HS làm ?1 (điền bút chì, 1 HS lên
bảng điền).

- HS đọc nhận xét SGK <122>.
Hoạt động của Thầy Hoạt động của học sinh
- Đưa hình 112 SGK hướng dẫn HS đọc
bài đọc thêm.

- Yêu cầu HS về nhà đọc lại để hiểu rõ
hơn.

3. DIỆN TÍCH MẶT CẦU
- Bằng thực nghiệm, người ta thấy diện
tích mặt cầu gấp 4 lần diện tích hình tròn
lớn của hình cầu.
S = 4πR
2
mà 2R = d ⇒ S = πd
2
.
S = 4πR
2
hay S = πd
2
VD1: Tính diện tích mặt cầu có đường
kính 42 cm.
- Yêu cầu HS tính.
- VD2: <tr.122 SGK>.

S mặt cầu = 36 cm
2
.
Tính đường kính của mặt cầu thứ 2 có diện
tích gấp 3 lần diện tích mặt cầu này.
- Ta cần tính gì đầu tiên ?
HS nêu cách tính:
S mặt cầu = πd
2
= π. 42
2
= 1764π (cm

2
).
Cần tính diện tích mặt cầu thứ 2.
36. 3 = 108 (cm
2
).
Ta có:
S mặt cầu = πd
2
108 = 3,14. d
2
⇒ d
2

≈≈
14,3
108
34,39
⇒ d = 5,86 (cm).
4. Củng cố.
Hoạt động của Thầy Hoạt động của học sinh
Bài 31
<bảng phụ>.
Bài 32:
Đề bài và hình vẽ trên bảng phụ.

Áp dụng ct: S = 4πR
2
.
Hai HS

lên bảng điền.áp dụng công thức:
S = 4πR
2
.
Bài 32:
Diện tích xung quanh hình trụ là:
S trụ = 2πr. h = 2π r . 2r = 4π r
2
.
Diện tích hai mặt bán cầu chính bằng
diện tích mặt cầu.
S mặt cầu = 4π r
2
.
Vậy diện tích bề mặt cả trong lẫn ngoài
của khối gỗ là:
S trụ + S mặt cầu = 4πr
2
+ 4πr
2
=
8πr
2
.
5. HDVN. `
- Nắm vững các khái niệm về hình cầu.
- Nắm chắc công thức tính diện tích mặt cầu.
- BTVN: 33 <125>. 27, 28, 29 <128 SBT>.
Soạn:
Giảng:

Tiết 64


H×nh cÇu DiÖn tÝch mÆt cÇu vµ thÓ tÝch h×nh cÇu
A. MỤC TIÊU:
- Kiến thức: Củng cố các khái niệm của hình cầu, công thức tính diện tích mặt cầu.
Hiểu cách hình thành công thức tính thể tích hình cầu, nắm vững công thức và biết áp
dụng vào bài tập.
- Kĩ năng : Thấy được ứng dụng thực tế của hình cầu.
- Thái độ : Rèn luyện tính cẩn thận cho HS.
B. CHUẨN BỊ:
B.phô, compa, thíc, qu¶ cÇu, cèc h×nh trô

C. TIẾN TRÌNH DẠY HỌC

1. Tổ chức: 9A
9B
9C
2. Kiểm tra bài cũ:
Hoạt động của Thầy Hoạt động của học sinh
HS1: Khi cắt mặt cầu bởi một mặt phẳng
Hoạt động của Thầy Hoạt động của học sinh
ta được mặt cắt là hình gì ? Thế nào là
đường tròn lớn của hình cầu.
- Làm bài tập 33 <125 SGK>:
1 cột
→
chuyển thành dòng.
- HS2: Trong các hình sau đây, hình nào
có diện tích lớn nhất:

A. hình tròn bán kính 2 cm.
B. Hình vuông có độ dài cạnh 3,5 cm.
C. Tam giác có độ dài các cạnh là 3, 4, 5
(tam giác vuông).
D. Nửa mặt cầu bán kính 4 cm.
Đường
kính
Độ dài
đường
tròn
lớn
Diện
tích
Thể
tích
Quả
bóng
gôn
42,7
mm
134,0
8
mm
5725
mm
2
.
- HS2:
S
(A)

= πR
2
= π. 2
2
= 4π (cm
2
).
S
(B)
= 3,5. 3,5 = 12,25 (cm
2
).
S
C
=
2
4.3
= 6 (cm
2
)
S
(D)
=
2
1
4π4
2
= 32π (cm
2
).

Vậy S
(D)
lớn nhất.
3. Bài mới
Hoạt động của Thầy Hoạt động của học sinh
4. THỂ TÍCH HÌNH CẦU
- GV giới thiệu dụng cụ thực hành.
- GV thao tác thực hành SGK.
- Em có nhận xét gì về độ cao của cột
nước còn lại trung bình so với chiều cao
với chiều của bình.
Vậy thể tích của hình cầu so với thể
tích của hình trụ như thế nào ?
- Thể tích hình trụ được tính theo công
thức nào ?
- Vật thể tích hình cầu được tính như thế
HS:
+ Độ cao của nước bằng 1/3 chiều cao
của bình.
⇒ V hình cầu bằng 2/3 thể tích của
hình trụ.
V
trụ
= πR
2
. 2R = 2πR
3
.
V cầu =
3

2
V trụ =
3
2
. 2πR
3
=
3
4
πR
3
.
1 HS đọc to đề bài.
1 HS tóm tắt đề bài.
d = 22 cm = 2,2 dm.
Nước chiếm
3
2
V cầu.
Tính số lít nước ?
Giải:
Thể tích hình cầu là:
Hoạt động của Thầy Hoạt động của học sinh
nào ?
Ví dụ <124 SGK>.

- Hãy nêu cách tính.
- GV yêu cầu 1 HS lên bảng tính.
- GV giới thiệu công thức tính thể tích
hình cầu theo đường kính.

V =
3
4
πR
3
=
3
4
π
3
2






d
=
3
4
π.
8
3
d
=
6
1
πd
3

.
- Nếu biết đường kính hình cầu thì sử dụng
công thức này.
V =
3
4
πR
3
=
6
1
πd
3
= 5,57 (dm
3
).
Lượng nước ít nhất cần phải có là:

3
2
. 5,57 = 3,71 (lít).
- Công thức tính thể tích hình cầu:
V =
3
4
πR
3
- Công thức tính thể tích hình cầu theo
đường kính.
V =

6
1
πd
3
4. Củng cố.
Hoạt động của Thầy Hoạt động của học sinh
Bài tập 31 SGK – 124
Bán kính
h cầu
0,3 mm 6,21 dm 0,283 m 100 km 6 km 50 dam
Thể tích
h cầu
0,13 mm
3
1002,64
dm
3
0,095 m
3
904,32
km
3
523333
dam
3
.
Bài 30 <124 SGK>.
- Hãy tính R để chọn kết quả.
HS tóm tắt đề bài:
V = 113

7
1
(cm
3
) Xác định bán kính
R.
(A) 2 cm ; (B) 3 cm ; (C) 5 cm.
(D) 6 cm ; (E) 1 kết quả khác.
HS tính:
Từ V =
3
4
πR
3
⇒ R
3
=
π
4
3V
⇒ R =
3
4
3
π
V
⇒ R =
3
7
22

.4
7
792
.3
R =
3
27
= 3.
⇒ Chọn (B) 3 cm.
Hoạt động của Thầy Hoạt động của học sinh
Bài tập: Điền vào chỗ ( ):
a) Công thức tính diện tích hình tròn
(O; R): S =
b) Công thức tính diện tích mặt cầu
(O; R) : S mặt cầu =
c) Công thức tính thể tích hình cầu
(O; R) : V cầu =
1 HS lên bảng điền.
a) πR
2
.
b) 4πR
2
hoặc = πd
2
.
c)
3
4
πR

3
hoặc
6
1
πd
3
.
5. HDVN. `
- Nắm cững các công thức trong bài.
- BTVN: 35, 36, 37 <126 SGK> ; 30, 31 <129, 130 SBT>.