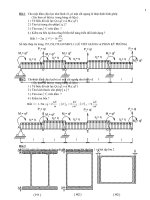
 Thay các số liệu và đặt phản lực liên kết thay cho các gối tựa, ta có hình sau:
 Xác định phản lực tại các gối tựa:
- Theo các điều kiện cân bằng ta có:
+ Tổng momen đối với điểm B bằng 0:
3qa.1,5a + 2qa.a + qa
2
- V
D
.2a = 0
 V
D
= 15a
+ Tổng momen đối với điểm D bằng 0:
3qa.1,5a + V
B
.2a + qa
2
– 2qa
2
= 0
 V
B
= -19a
+ Kiểm tra lại ta có:
P + V
D
– V
B
– 2qa = 12a + 15a – 19a – 8a = 0
 Như vậy các phản lực đã đúng.
 Chia đoạn:

Chia đoạn sao cho mỗi đoạn không có sự thay đổi đột ngột về ngoại lực và về
phương của trục thanh. Ở đây thanh chia thành ba đoạn AB, BC và CD (như
hình):
Trang 1
 Viết biểu thức nội lực cho từng đoạn:
(1) Đoạn AB: Xét mặt cắt 1-1với tọa độ z
1
bất kì (0a) Giữ lại phần thanh bên
trái mặt cắt 1-1 và đặt vào trọng tâm O
1
của mặt cắt đó các thành phần nội lực:
(1)
( )
z
N z
;
(1)
( )
y
Q z
và
(1)
( )
x
M z
.
- Viết điều kiện cân bằng đối với phần thanh được giữ lại:\
+ Tổng lực theo phương ngang
N
z

(1)
(z) = 0
+ Tổng lực theo phương đứng
Q
y
(1)
(z) – P =0  Q
y
(1)
(z) = P = 12a
+Tổng momen
P.z
1
– M
x
(1)
(z) = 0  M
x
(1)
(z) = P.z
1
= 12az
1
(2) Đoạn BC: Xét mặt cắt 2-2 với z
2
bất kì (1,5a2,5a). Giữ lại phần thanh bên
trái mặt cắt 2-2 và đặt vào trọng tâm O
2
của mặt cắt đó các thành phần nội lực:
(2)

( )
z
N z
;
(2)
( )
y
Q z
và
(2)
( )
x
M z
.
Trang 2
Tương tự, ta có:
+ Tổng lực theo phương ngang
N
z
(2)
(z) = 0
+ Tổng lực theo phương đứng
Q
y
(2)
(z) – P + V
B
+ q(z
2
– 1,5a) = 0

 Q
y
(2)
(z) = P – q(z
2
– 1,5a) – V
B

+ Tổng momen
–V
B
.(z
2
– 1,5a) + P.z
2
– q((z
2
– 1,5a)
2
)/2 – M
x
(2)
(z) = 0
 M
x
(2)
(z) = P.z
2
–V
B

.(z
2
– 1,5a) – q((z2 – 1,5a)
2
)/2
(3) Đoạn CD: Xét mặt cắt 3-3 với z
3
bất kì ( 2,5a3,5a). Giữ lại phần thanh bên
phải mặt cắt 3-3 và đặt vào trọng tâm O
3
của mặt cắt đó các thành phần nội lực:
(3)
( )
z
N z
;
(3)
( )
y
Q z
và
(3)
( )
x
M z
.
Tương tự, ta có:
+ Tổng lực theo phương ngang
N
z

(3)
(z) = 0
+ Tổng lực theo phương đứng
Q
y
(3)
(z) + V
D
– q(3,5 – z
3
) = 0
 Q
y
(3)
(z) = q(3,5 – z
3
) – V
D
+ Tổng momen
M
x
(3)
(z) – V
D
.(3,5a – z
3
) + q((3,5 – z
3
)
2

)/2
 M
x
(3)
(z) = V
D
.(3,5a – z
3
) – q((3,5 – z
3
)
2
)/2
Trang 3
 Phân tích các biểu thức nội lực:
Với a = 1
(1) Đoạn AB:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
là hằng số: Q
y
= P = 12 kN
+ M
x
là đường bậc nhất:
Tại A (z
1

= 0), ta có: M
x
(1)
(z) = 0 kNm
Tại B (z
1
= 1,5), ta có: M
x
(1)
(z) = 18 kNm
(2) Đoạn BC:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
là đường bậc nhất:
Tại B (z = 1,5), ta có: Q
y
(2)
(z) = -7 kN
Tại C (z = 2,5), ta có: Q
y
(2)
(z) = -11 kN
+ M
x
là đường cong bậc hai:
Tại B (z = 1,5), ta có: M
x

(2)
(z) = 18 kNm
Tại C (z = 2,5), ta có: M
x
(2)
(z) = 9 kNm
Do đó M
x
quay bề lõm về phía âm của biểu đồ.
(3) Đoạn CD:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
là đường bậc nhất:
Tại C (z = 2,5), ta có: Q
y
(3)
(z) = -11 kN
Tại D (z = 3,5), ta có: Q
y
(3)
(z) = -15 kN
+ M
x
là đường cong bậc hai:
Tại C (z = 2,5), ta có: M
x
(3)

(z) = 13

kNm
Tại D (z = 3,5), ta có: M
x
(3)
(z) = 0 kNm
Với việc tiến hành phân tích các biểu thức nội lực vừa nêu trên, ta tiến hành vẽ
các biểu đồ nội lực.
 Biểu đồ lực dọc N
z
, lực cắt Q
y
và momen uốn M
x
:
Trang 4
 Nhận xét:
+ Đoạn AB không có lực phân bố nên lực cắt là hằng số  momen uốn là
đường bậc nhất.
+ Đoạn BD có lực phân bố đều nên lực cắt là đường bậc nhất  momen uốn là
đường cong bậc hai.
+ Tại A có lực tập trung P = 12 kN, nên biểu đồ lực cắt có bước nhảy.
+ Tại C có momen tập trung M = 4 kNm, nên biểu đồ momen uốn có bước
nhảy.
Trang 5
 Thay các số liệu và đặt phản lực liên kết thay cho ngàm:
 Tìm phản lực V
D
, H

D
và momen tại D.
+ Tổng lực theo phương ngang bằng 0:

H
D
= 0
+ Tổng momen đối với điểm D bằng 0:
M + M
D
+ P – q
o
.(1/2)a.(5/3)a = 0
 M
D
= (5/6).q
o
a
2
– Pa – M = – (7/6)q
o
a
2

 M
D
có chiều ngược lại
+ Tổng lực theo phương đứng bằng 0:
P + V
D

– (1/2)q
o
a = 0
 V
D
= (1/2)q
o
a – P = – (1/2)q
o
a
 V
D
có chiều ngược lại
 Chia đoạn:
- Thanh chia thành 3 đoạn AB, BC và CD. Ta có hình như bên dưới:
Trang 6

Viết biểu thức nội lực cho từng đoạn thanh:
(1) Đoạn AB: Xét mặt cắt 1-1với tọa độ z
1
bất kì (00,5a). Giữ lại phần thanh
bên trái mặt cắt 1-1 và đặt vào trọng tâm O
1
của mặt cắt đó các thành phần nội
lực:
(1)
( )
z
N z
;

(1)
( )
y
Q z
và
(1)
( )
x
M z
.
0
- Viết điều kiện cân bằng đối với phần thanh được giữ lại:
M - M
x
(1)
(z) = 0  M
x
(1)
(z) = M
N
z
(1)
(z) = 0
Q
y
(1)
(z) = 0
(2) Đoạn BC: Xét mặt cắt 2-2 với z
2
bất kì (0,5a  1,5a). Giữ lại phần thanh

bên phải mặt cắt 2-2 và đặt vào trọng tâm O
2
của mặt cắt đó các thành phần nội
lực:
(2)
( )
z
N z
;
(2)
( )
y
Q z
và
(2)
( )
x
M z
.
- Tương tự, ta có:
N
z
(2)
(z) = 0
Q
y
(2)
(z) = (q
z
(2,5a – a – z

2
))/2 – P + V
D
với q
z
= (q
o
((1,5a-z
2
)))/a
 Q
y
(2)
(z) = (q
o
(1,5a – z
2
)
2
)/2a – P + V
D
M
x
(2)
(z) = - (q
o
(1,5a – z
2
)
3

)/6 + P(1,5a – z
2
) + M
D
– V
D
(2,5a – z
2
)
(3) Đoạn CD: Xét mặt cắt 3-3 với z
3
bất kì (1,5a  2,5a). Giữ lại phần thanh
bên phải mặt cắt 3-3 và đặt vào trọng tâm O
3
của mặt cắt đó các thành phần nội
lực:
(3)
( )
z
N z
;
(3)
( )
y
Q z
và
(3)
( )
x
M z

.
Trang 7
Tương tự, ta có:
N
z
(3)
(z) = 0
Q
y
(3)
(z) = V
D
M
x
(3)
(z) + V
D
(2,5a-z
3
) – M
D
= 0
 M
x
(3)
(z) = M
D
– V
D
(2,5a-z

3
)
 Phân tích các biểu thức nội lực.
Với a = 1
(1) Đoạn AB:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
không tồn tại trong toàn đoạn.
+ M
x
là hằng số với: M
x
= 8

kNm
(2) Đoạn BC:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
là đường cong bậc 2: Q
y
(2)
(z) = (q
o
(1,5a – z

2
)
2
)/2 – P + V
D

Tại B (z = 0,5a) thì: Q
y
(2)
(z) = 0
Tại C (z = 1,5a) thì:

Q
y
(2)
(z) = 4 kN
Xét cực trị của đường cong:
dQ
y
(2)
(z)/dz = – q
o
(1,5a – z2) = 0  z
2
= 1,5 m
Như vậy, điểm cực trị sẽ nằm trong đoạn BC, tại C (z = 1,5a).
d
2
Q
y

(2)
(z) /dz
2
= q
o
> 0
Như vậy bề lõm của Q
y
sẽ quay về phía dương của biểu đồ.
+ M
x
là đường cong bậc 3:
M
x
(2)
(z) = - (q
o
(1,5a – z
2
)
3
)/6 + P(1,5a – z
2
) + M
D
– V
D
(2,5a – z
2
)

Tại B (z = 0,5a), thì:
Trang 8
M
x
(2)
(z) = 8 kNm
Tại C (z = 1,5a), thì:
M
x
(2)
(z) = 16/3 kNm
Vì trong đoạn BC, lực cắt Q
y
tại điểm B (z = 0,5a) bằng 0 nên biểu đồ M
x
đạt
cực trị. Mặt khác, lực cắt Q
y
phân bố trong đoạn này luôn âm nên đường biểu
diễn M
x
quay bề lõm về phía trên.
(3) Đoạn CD:
+ N
z
không tồn tại trong toàn đoạn.
+ Q
y
là hằng số, với Q
y

(3)
(z) = 4

kN
+ M
x
là đường bậc nhất M
x
(3)
(z) = M
D
– V
D
(2,5-z
3
)
Tại C (z = 1,5a), ta có: M
x
(3)
(z) = 16/3

kNm
Tại D (z = 2,5a), ta có: M
x
(3)
(z) = 28/3

kNm
- Với những phân tích trên, ta tiến hành vẽ biểu đồ nội lực.
 Biểu đồ nội lực.

Trang 9
 Nhận xét:
+ Đoạn AB lực cắt không tồn tại  momen uốn là hằng số. Đoạn CD lực cắt là
hằng số  momen uốn là đường bậc nhất.
+ Đoạn BC có lực phân bố là đường bậc nhất  lực cắt là đường bậc hai 
momen uốn là đường bậc ba.
+ Tại C có lực tập trung P = 8 kN nên biểu đồ lực cắt có bước nhảy.
+ Tại A có momen tập trung M = 8 kNm nên biểu đồ momen uốn có bước nhảy.
Trang 10
 Thay các số liệu và đặt phản lực liên kết thay cho các gối tựa, ta có hình sau:
 Tính các phản lực H
A
, H
E
và V
D
.
+ Tổng lực theo phương ngang bằng 0:
H
A
+ H
E
– qa = 0  H
A
+ H
E
= qa kN
+ Tổng lực theo phương đứng bằng 0: - H
E
a +qa

2
/2 – V
D
3a + M – Pa + 2qa
2
V
D
+ P – 2qa = 0  V
D
= - 4qa kN
 V
D
có chiều ngược lại
+ Tổng momen tại A bằng 0:
- H
E
a +qa
2
/2 – V
D
3a + M – Pa + 2qa
2
= 0  H
E
= (21/2)qa kN
 H
A
= -(19/2)qa
 H
A

có chiều ngược lại
 Chia đoạn.
Chia khung thành 4 đoạn AB, BC, CD, và CE như hình bên dưới:
Trang 11
 Viết biểu thức nội lực cho từng đoạn thanh.
(1) Đoạn AB: Xét mặt cắt 1-1với tọa độ z
1
bất kì (0a). Giữ lại phần thanh bên
trái mặt cắt 1-1 và đặt vào trọng tâm O
1
của mặt cắt đó các thành phần nội lực:
(1)
( )
z
N z
;
(1)
( )
y
Q z
và
(1)
( )
x
M z
.
- Viết điều kiện cân bằng đối với phần thanh được giữ lại:
- M
x
(1)

(z) - (q/2)z
1
2
= 0  M
x
(1)
(z) = – (q/2)z
1
2
N
z
(1)
(z) – H
A
= 0  N
z
(1)
(z) = H
A
– Q
y
(1)
(z) – qz
1
= 0  Q
y
(1)
(z) = - qz
1
Suy ra: M

X
va Q
y
có chiều ngược lại
(2) Đoạn BC: Xét mặt cắt 2-2 với z
2
bất kì (a2a). Giữ lại phần thanh bên trái
mặt cắt 2-2 và đặt vào trọng tâm O
2
của mặt cắt đó các thành phần nội lực:
(2)
( )
z
N z
;
(2)
( )
y
Q z
và
(2)
( )
x
M z
.
Trang 12
- Tương tự, ta có:
N
z
(2)

(z) – H
A
= 0
Q
y
(2)
(z) + qz
2
– P = 0
–M
x
(2)
(z) – q(z
2
)
2
/2 + P(z
2
– a) = 0
Suy ra:
N
z
(2)
(z) = H
A
= (19/2)qa
Q
y
(2)
(z) = P – qz

2

M
x
(2)
(z) = P(z
2
– a) – q(z
2
)
2
/2
(3) Đoạn CD: Xét mặt cắt 3-3 với z
3
bất kì (2a3a). Giữ lại phần thanh bên
phải mặt cắt 3-3 và đặt vào trọng tâm O
3
của mặt cắt đó các thành phần nội lực:
(3)
( )
z
N z
;
(3)
( )
y
Q z
và
(3)
( )

x
M z
.
Tương tự, ta có:
N
z
(3)
(z) = 0
Q
y
(3)
(z) – V
D
=0
M
x
(3)
(z) +V
D
(3 – z
3
)
Trang 13
Suy ra:
N
z
(3)
(z) = 0
Q
y

(3)
(z) = V
D
M
x
(3)
(z) = – V
D
(3 – z
3
)
(4) Đoạn EC: Xét mặt cắt 4-4 với z4 bất kì (0a). Giữ lại phần thanh phía dưới
mặt cắt 4-4 và đặt vào trọng tâm O
4
của mặt cắt đó các thành phần nội lực:
(4)
( )
z
N z
;
(4)
( )
y
Q z
và
(4)
( )
x
M z
.

Tương tự, ta có:
N
z
(4)
(z) = 0
Q
y
(4)
(z) + H
E
– qz
4
= 0
– M
x
(4)
(z) – H
E
z
4
+ q(z
4
)
2
/2 = 0
Suy ra:
N
z
(4)
(z) = 0

Q
y
(4)
(z) = qz
4
– H
E
M
x
(4)
(z) = – H
E
z
4
+ q(z
4
)
2
/2
 Phân tích các biểu thức nội lực.
Với a = 1
(1) Đoạn AB:
+ N
z
là hằng số trong toàn đoạn với: N
z
(1)
(z) = H
A
= (19/2)qa = 57/2 kN

Trang 14
+ Q
y
là đường bậc nhất: Q
y
(1)
(z) = - qz
1
Tại A (z = 0)  Q
y
= 0
Tại B (z = 1)  Q
y
= 3kN

kN
+ M
x
là đường cong bậc hai: M
x
(1)
(z) = –(q/2)z
1
2
Tại A (z = 0) M
x
= 0

Tại B (z = 1) Mx = -3/2 kNm
Xét cực trị của đường cong:

(dM
x
(1)
(z))/dz = -qz
1
= 0  z
1
= 0
Như vậy, điểm cực trị sẽ nằm trong đoạn AB, tại A (z = 0).
(d
2
M
x
(1)
(z))/dz
2
= -q <0
Như vậy bề lõm của M
x
sẽ quay về phía âm của biểu đồ.
(2) Đoạn BC:
+ N
z
là hằng số trong toàn đoạn với: N
z
(2)
(z) = (19/2)qa = 57/2 kN
+ Q
y
là đường bậc nhất: Q

y
(2)
(z) = P – qz
2
Tại B (z = 1) thì: Q
y
= 15 kN

Tại C (z = 2) thì: Q
y
= 12kN

+ M
x
là đường cong bậc hai: M
x
(1)
(z) = P(z
2
– a) – q(z
2
)
2
/2
Tại B (z = 1)  M
x
= -3/2

kNm
Tại C (z = 2)  M

x
= 12

kNm
Xét cực trị của đường cong:
(dM
x
(2)
(z))/dz = P – qz
2
= 0 z
2
= 6m
Như vậy, điểm cực trị nếu có sẽ không nằm trong đoạn BC.
(d
2
M
x
(2)
(z))/dz
2
= -q <0
Như vậy bề lõm của M
x
sẽ quay về phía âm của biểu đồ.
(3) Đoạn CD:
+ N
z
không tồn tại trong toàn đoạn.
+ Q

y
là hằng số với: Q
y
(3)
(z) = V
D
= 12

kN
+ M
x
là đường bậc nhất: M
x
(3)
(z) = – V
D
(3 – z
3
)
Tại C (z = 2)  M
x
= -12

kNm
Tại D (z = 3)  M
x
= 0
(4) Đoạn EC:
+ N
z

là không tồn tại trong toàn đoạn.
+ Q
y
là đường bậc nhất: Q
y
(4)
(z) = qz
4
– H
E

Tại E (z = 0) thì: Q
y
= -63/2


kN
Tại C (z = 1) thì: Q
y
= -57/2

kN
+ M
x
là đường cong bậc hai: M
x
(4)
(z) = – H
E
z

4
+ q(z
4
)
2
/2
Tại E (z = 0)  M
x
= 0

Tại C (z = 1)  M
x
= -30

kNm
(d
2
M
x
(4)
(z))/dz
2
= q > 0
Trang 15
Như vậy bề lõm của M
x
sẽ quay về phía dương của biểu đồ.
- Với những phân tích trên, ta tiến hành vẽ biểu đồ nội lực.
 Biểu đồ nội lực.
Biểu đồ lực cắt Q

y
và momen uốn M
x
được biểu diễn ở bên dưới.
Trang 16
Xét cân bằng tại nút C:
Ta thấy rằng, nút C đã cân bằng.
 Nhận xét:
+ Đoạn CD không có lực phân bố  lực cắt là hằng số  momen uốn là đường
bậc nhất. Đoạn AC và EC có lực phân bố đều  lực cắt là đường bậc nhất 
momen uốn là đường cong bậc hai.
+ Tại B có lực tập trung  biểu đồ lực cắt có bước nhảy. Tại C có momen tập
trung  biểu đồ momen uốn có bước nhảy.
Trang 17
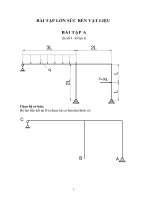
 Đặt số liệu, hệ trục tọa độ và kí hiệu các mặt phẳng chứa các thanh.
Ta thực hiện việc chia các mặt cắt theo các mặt phẳng, sẽ có được như hình bên
dưới.
Trang 18
 Viết các biểu thức nội lực (chỉ xét lực dọc N
z
, momen uốn M
x
và momen xoắn
M
z
).
(1) Đoạn AB: dời lực P từ điểm C về B, tại B sẽ có lực P và một momen nằm
trong mặt phẳng
( )
α

theo chiều kim đồng hồ là M
P
= 18 kNm. Dời momen M
về B, ta nhận thấy momen M này làm xoắn thanh AB.
- Xét mặt cắt 1-1 (nằm trong mặt phẳng
( )
γ
) với z bất kì (
0 1z≤ ≤
). Giữ lại
phần thanh phía bên phải mặt cắt 1-1 và đặt vào trọng tâm O
1
của mặt cắt đó các
thành phần nội lực:
(1)
( )
z
N z
;
(1)
( )
x
M z
.
Ta có các phương trình cân bằng sau:
(1)
0 ( ) 0
z
Z N z P
= ⇔ + =

∑
( )
2
(1)
1
1
/ 0 ( ) 0
2
x
z
M k M z q
−
= ⇔ + =
∑
Suy ra:
(1)
( )
z
N z P= −
( )
2
(1)
1
( )
2
x
z
M z q
−
= −

- Xét mặt cắt 2-2 (nằm trong mặt phẳng
( )
α
) với z bất kì (
0 1z≤ ≤
). Giữ lại
phần thanh phía bên phải mặt cắt 2-2 và đặt vào trọng tâm O
2
của mặt cắt đó các
thành phần nội lực:
(2)
( )
z
N z
;
(2)
( )
y
M z
.
Trang 19
Ta có các phương trình cân bằng sau:
(2)
0 ( ) 0
z
Z N z P
= ⇔ + =
∑
(2)
2

/ 0 ( ) 0
y P
M k M z M
= ⇔ − =
∑
Suy ra:
(2)
( )
z
N z P= −
(2)
( )
y P
M z M
=
Ngoài ra đoạn thanh AB còn chịu một momen xoắn M với
6
z
M
= −
kNm.
(2) Đoạn CB:
- Xét mặt cắt 3-3 (nằm trong mặt phẳng
( )
α
) với z bất kì (
0 1z≤ ≤
). Giữ lại
phần thanh phía bên trái mặt cắt 3-3 và đặt vào trọng tâm O
3

của mặt cắt đó các
thành phần nội lực:
(3)
( )
x
N z
;
(3)
( )
y
M z
.
Ta có các phương trình cân bằng sau:
Trang 20
(3)
0 ( ) 0
x
X N z
= ⇔ =
∑
(3)
3
/ 0 ( ) 0
y
M k M z Pz
= ⇔ + =
∑
Suy ra:
(3)
( ) 0

x
N z
=
(3)
( )
y
M z Pz
= −
- Xét mặt cắt 4-4 (nằm trong mặt phẳng
( )
β
) với z bất kì (
0 1z≤ ≤
). Giữ lại
phần thanh phía bên trái mặt cắt 4-4 và đặt vào trọng tâm O
4
của mặt cắt đó các
thành phần nội lực:
(4)
( )
x
N z
;
(4)
( )
z
M z
.
Ta có các phương trình cân bằng sau:
(4)

0 ( ) 0
x
X N z
= ⇔ =
∑
(4)
4
/ 0 ( ) 0
z
M k M z M
= ⇔ − =
∑
Suy ra:
(4)
( ) 0
x
N z
=
(4)
( )
z
M z M=
 Phân tích các biểu thức nội lực.
(1) Đoạn AB:
+ N
z
là hằng số trong toàn thanh với
(1)
( ) 18
z z

N N z P= = − = −
kN
Trong mặt phẳng
( )
γ
:
+ M
x
là đường bậc hai:
( )
2
(1)
1
( )
2
x
z
M z q
−
= −
Tại A (z = 0) 
( )
2
(1)
1 0
3
(0) 3
2 2
x x
M M

−
= = − = −
kNm
Trang 21
Tại B (z = 1) 
( )
2
(1)
1 1
(1) 3 0
2
x x
M M
−
= = − =
Xét:
2 (1)
2
( )
0
x
d M z
q
dz
= − <
Vậy bề lõm hướng về phía âm của biểu đồ.
+ Ngoài ra đoạn thanh AB còn chịu một momen xoắn M với
6
z
M

= −
kNm.
+ Trong mặt phẳng
( )
α
:
M
y
là hằng số trong toàn thanh với
(2)
( ) 18
y y
M M z
= =
kNm
(2) Đoạn CB:
Trong mặt phẳng
( )
α
:
+ N
x
không tồn tại trong toàn đoạn.
+ M
y
là đường bậc nhất:
(3)
( )
y
M z Pz

= −
Tại C (z = 0) 
(3)
( ) 0
y y
M M z
= =
Tại B (z = 1) 
(3)
( ) 18
y y
M M z P
= = = −
kNm
Trong mặt phẳng
( )
β
:
+ N
x
không tồn tại trong toàn đoạn.
+ M
z
là hằng số trong toàn đoạn với
(4)
( ) 6
z z
M M z M= = =
kNm
- Với những phân tích trên, ta tiến hành vẽ biểu đồ nội lực.

 LỰC DỌC:
 MOMEN UỐN:
Trang 22
 MOMEN XOẮN:
Trang 23