KT hinh 7 chuong 2 ma tran de va dap an
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (108.35 KB, 3 trang )
x
(H.1)
140
°
130
°
K
I
P
N
M
kiĨm tra ch¬ng ii - h×nh häc 7
A Mơc tiªu :
1 Về kiến thức:
Hệ thống các kiến thức về tam giác: tính chất tổng ba góc của một tam giác , tính
chất góc ngoài của tam giác
BiÕt c¸c kh¸i niƯm tam gi¸c c©n, tam gi¸c vu«ng c©n, tam gi¸c ®Ịu vµ c¸c tÝnh chÊt cđa
c¸c tam gi¸c ®Ỉc biƯt.
BiÕt c¸c TH b»ng nhau cđa tam gi¸c, c¸c Th b»ng nhau cđa tam gi¸c vu«ng.
2 Về kó năng:
HiĨu vµ vËn dơng ®ỵc c¸c ®Þnh lÝ vµo trong tÝnh to¸n
+Đo đạt, vẽ hình, tính toán, chứng minh hình học.
+Kỹ năng quan sát, tính cẩn thận, chính xác.
VËn dơng ®ỵc c¸c tÝnh chÊt cđa tam gi¸c c©n vµo trong tÝnh to¸n ®¬n gi¶n.
3 Th¸i ®é
Trung thùc, cÈn thËn khi lµm bµi.
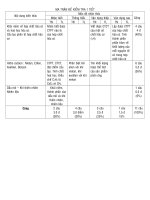
B. Ma trËn ®Ị kiĨm tra
Møc ®é
Chn
NhËn biÕt Th«ng hiĨu
VËn dơng
thÊp
VËn dơng
cao
Tỉng
1. Tỉng ba gãc cđa mét tam gi¸c
TN TN TN TL TN TL TN TL
1
0,
5
1
0,
5
2. Hai tam gi¸c b»ng nhau
1
0,5
1
0,5
2
3,0
4
4,
0
3. C¸c d¹ng tam gi¸c ®Ỉc biƯt.
2
1,0
1
0,5
1
1,5
2
2,5
6
4,5
Tỉng
3
1,5
3
1,5
3
4,5
2
2,5
11
10,0
C. §Ị bµi
PhÇn I. Tr¾c nghiƯm: (3,0 ®iĨm)
H·y khoanh trßn ch÷ c¸i ®øng tríc c©u tr¶ lêi mµ em chän.
Bµi 1: Quan s¸t (H.1) vµ chän gi¸ trÞ ®óng
cđa x (biÕt IK // MN)
A. 100
0
; B. 90
0
; C. 80
0
; D. 50
0
Bµi 2: Quan s¸t (H.2) vµ cho biÕt
®¼ng thøc nµo viÕt ®óng theo quy íc:
A.
∆
PQR =
∆
DEF ; C.
∆
PQR =
∆
EDF
B.
∆
PQR =
∆
DFE ; D.
∆
PQR =
∆
EFD
Bµi 3 NÕu tam gi¸c ABC
cã AB = 13 cm, AC = 12 cm , BC = 5 cm
th× tam gi¸c ABC:
A. Lµ tam gi¸c vu«ng t¹i A C. Lµ tam gi¸c vu«ng t¹i C
B. Lµ tam gi¸c vu«ng t¹i B D. Kh«ng ph¶i lµ tam gi¸c vu«ng
Bµi 4 Quan s¸t (H.3) vµ chän gi¸ trÞ ®óng cđa y:
A. y = 9 B. y = 25
C. y = 225 D. y = 15
Bµi 5: Góc ngồi của tam giác lín h¬n:
A. Mçi gãc trong kh«ng kỊ víi nã B. Góc trong kề với nó.
C. Tỉng cđa hai góc trong kh«ng kề với nó D. Tổng ba góc trong của tam
giác.
Bµi 6: Trong tam giác đều, mỗi góc bằng :
A. 45
0
B. 60
0
C. 90
0
D. 180
0
II. Tù ln: (7,0 ®iĨm)
Bµi 7: (6.0 ®iĨm): Cho gãc nhän xOy Vµ M lµ mét ®iĨm thc tia ph©n gi¸c cđa gãc
xOy. KỴ MA vu«ng gãc víi Ox ( A
∈
Ox), MB vu«ng gãc víi Oy ( B
∈
Oy)
a. Chøng minh: MA = MB.
b. Tam gi¸c OAB lµ tam gi¸c g×? V× sao?
c. §êng th¼ng BM c¾t Ox t¹i D, ®êng th¼ng AM c¾t Oy t¹i E. Chøng
minh: MD = ME.
d. Chøng minh OM
⊥
DE
Bµi 8(1.0 ®iĨm): Cho tam gi¸c ABC cã M lµ trung ®iĨm cđa c¹nh BC vµ AM =
1
2
BC,
gãc C =15
0
. TÝnh sè ®o gãc B.
D. §¸p ¸n & biĨu chÊm:
PhÇn I. Tr¾c nghiƯm ( 3 ®iĨm )
Mçi bµi lùa chän ®óng ®¸p ¸n ®ỵc 0,5 ®iĨm
Bµi 1 2 3 4 5 6
§¸p ¸n B D C D A B
PhÇn II.Tù ln: ( 7 ®iĨm )
Bµi 7: (6,0 ®iĨm) Mçi c©u ®óng cho 1,5 ®iĨm
a) XÐt
∆
AMO vµ
∆
BMO cã:
AOM = BOM (v× OM lµ ph©n gi¸c)
OAM = OBM = 90
0
( v× MA
⊥
Ox; MB
⊥
Oy)
OM lµ c¹nh hun chung
(H.2)
80
°
60
°
40
°
60
°
F
E
D
R
Q
P
y
(H.3)
17
8
AMO =
BMO (cạnh huyền góc nhọn) (1,0 điểm)
MA = MB. (0,5 điểm)
b) Vì
AMO =
BMO
OA = OB (hai cạnh tơng ứng) (0,75 điểm)
Vậy
OAB là tam giác cân ( hai cạnh bằng nhau) (0,75 điểm)
c) Xét
AMD và
BMD có
DAM = EBM = 90
0
AM = BM ( suy ra từ
AMO =
BMO)
AMD = BME (hai góc đối đỉnh)
AMD =
BMD (g.c.g) (1,0 điểm)
MD = ME (0,5 điểm)
d)
AMD =
BMD
AD = BE (hai cạnh tơng ứng) (0,5 điểm)
Mà đã có OA = OB
Vậy suy ra OA + AD = OB + BE
OD = OE (0,5 điểm)
(vì A nằm giữa O và D, B nằm giữa O và E)
Vậy
ODE cân tại O
mà OM là phân giác nên OM là đờng cao
OM
DE (0,5 điểm)
Bài 8 (1.0điểm) Ghi GT và KL đầy đũ
Chứng minh đớc tam giác ABM cân tại M
Chứng minh đớc tam giác ACM cân tại M
Tinh đợc góc A = 90
0
tính đợc góc C = 85
0
A
C
B
M