DE KIEM TRA HOC KY II. TOAN 7
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (2.41 MB, 5 trang )
PHÒNG GIÁO DỤC & ĐÀO TẠO
HUYỆN TỨ KỲ
ĐỀ KIỂM TRA HỌC KỲ II
Năm học 2012-2013
MÔN : TOÁN – LỚP 7
Thời gian làm bài: 90 phút
(Đề này gồm 05 câu, 01 trang)
Câu 1 (1,5 điểm). Một giáo viên theo dõi thời gian làm một bài tập (tính theo
phút) của 40 học sinh lớp mình (em nào cũng làm được bài) và ghi lại như sau:
9 8 9 9 9 9 10 5 5 10
10 6 8 8 8 7 9 9 10 8
8 10 9 5 9 10 6 9 7 9
5 7 8 10 7 8 10 7 14 8
a) Dấu hiệu ở đây là gì?
b) Hãy lập bảng “tần số”.
c) Tính số trung bình cộng, tìm mốt của dấu hiệu và rút ra nhận xét.
Câu 2 (1,5 điểm). Cho đơn thức:
2 3
1 6 5
A xy . x yz . yz
3 7 4
a) Thu gọn đơn thức A.
b) Tính giá trị của đơn thức A tại x = -1; y = 2; z =
1
2
Câu 3 (1,0 điểm).
Cho đa thức:
B =
2 2 2 2
4x – 2xy + 3xy + 6xy – 5xy + 1– 7x + 2xy– 2
a) Thu gọn đa thức B.
b) Tìm đa thức C biết: C + B =
2 2 2
3x – xy + y – 4
Câu 4 (2,0 điểm).
Cho hai đa thức sau: f(x) = 1 – 3x + 2x
5
+ x
2
– x
3
+ 3x – 4 + 3x
2
;
g(x) = 2x
5
– x
3
+ 3x
2
– 2x – 6
a) Thu gọn và sắp xếp các hạng tử của đa thức f(x) theo luỹ thừa giảm dần
của biến.
b) Giá trị x = –1 có là nghiệm của đa thức f(x) không? Vì sao?
c) Tìm đa thức h(x) biết rằng: h(x) = f(x) – g(x)
d) Chứng tỏ rằng đa thức h(x) không có nghiệm trong R.
Câu 5 (4,0 điểm). Cho tam giác ABC vuông tại A, tia phân giác góc ACB cắt cạnh
AB tại D. Trên cạnh CB lấy điểm E sao cho CA = CE. Gọi M là giao điểm của hai
đường thẳng CA và ED.
a) Chứng minh
DE BC
;
b) Chứng minh AB = EM;
c) Chứng minh AE//MB;
d) Kẻ AH vuông góc với BC (H
BC). So sánh EH và EB.
======== Hết ========
T-DH01-HKII7-13
PHÒNG GIÁO DỤC & ĐÀO TẠO
HUYỆN TỨ KỲ
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KỲ II
Năm học 2012-2013
MÔN : TOÁN – LỚP 7
Thời gian làm bài: 90 phút
(Hướng dẫn chấm gồm 04 trang)
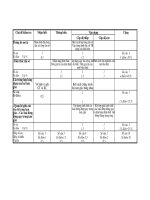
I. MA TRẬN ĐỀ KIỂM TRA
Vận dụng Cấp độ
Chủ đề
Nhận biết Thông hiểu
Cấp độ
thấp
Cấp độ cao
Cộng
1. Thống kê.
- Nhận biết được dấu
hiệu
Lập được bảng
”tần số”, tính
được giá trị trung
bình cộng, tìm
được mốt của dấu
hiệu và nhận xét
được số liệu
thống kê.
Số câu
Số điểm
Tỉ lệ %
1
0,25
2
1,25
3
1,5đ
=15%
2. Biểu thức
đại số
- Biết thu gọn các đơn
thức, đa thức.
- Nhận biết được một
số có là nghiệm của đa
thức hay không
- Hiểu các cộng
và trừ các đa thức
- Tính được giá
trị của biểu thức
đại số.
- Chứng minh
một đa thức
không có
nghiệm trong R
Số câu
Số điểm
Tỉ lệ %
4
2,25
3
1,75
1
0,5
8
4,5đ
=10%
3. Tam giác.
- Vẽ hình
- Hiểu các tính
chất của tam giác
cân
- Vận dụng được các trường
hợp bằng nhau của hai tam
giác, tính chất của hai tam
giác bằng nhau, tính chất
đường trung trực của đoạn
thảng, tính chất tam giác cân
để chứng minh
Số câu
Số điểm
Tỉ lệ %
0,5
3
2,5
3
3,0 đ
30%
4. Quan hệ
giữa các yếu
tố trong tam
giác
Vận dụng mối
quan hệ giữa
góc và cạnh đối
diện trong tam
giác để chứng
minh.
Số câu
Số điểm
Tỉ lệ %
1
1,0
1
1 đ
10 %
Tổng số câu
Tổng số điểm
Tỉ lệ %
5
2,5
25 %
5
3,5
35 %
3
2,5
25 %
2
1,5
15 %
15
10
100%
T-DH01-HKII7-13
II. ĐÁP ÁN, BIỂU ĐIỂM
BÀI Ý ĐÁP ÁN Điểm
a) 0,25 điểm
Dấu hiệu ở đây là thời gian làm một bài tập của mỗi học sinh.
0,25
b) 0,5 điểm
Bảng tần số:
Thời gian (x) 5 6 7 8 9 10
14
Tần số (n) 4 2 5 9 11
8 1 N=40
0,5
c) 0,75 điểm
5.4 6.2 7.5 8.9 9.11 10.8 14.1 332
X 8,3
40 40
0,25
M
0
= 9 0,25
Bài 1
(1,5đ)
Học sinh làm bài nhanh nhất mất 5 phút.
Học sinh làm bài chậm nhất mất 14 phút.
Đa số học sinh hoàn thành bài tập trong khoảng 8-10 phút
0,25
a) 0,75 điểm
Thu gọn
2 3 4 4 2
1 6 5 5
A xy . x yz . yz x y z
3 7 4 14
0,75
b) 0,75 điểm
Bài 2
(1,5 đ)
Tính A =
2
4 4
5 1
.( 1) .2 .
14 2
5 1 10
.1.16.
14 4 7
0,25
0,5
a) 0,5 điểm
B =
2 2 2 2
4x – 2xy + 3xy + 6xy – 5xy + 1– 7x + 2xy– 2
=
2 2 2 2
(4x – 7x ) (– 2xy + 6xy )+ (3xy – 5xy+ 2xy)
+ (1– 2)
=
2 2
3x 4xy 1
0,5
b) 0,5 điểm
Bài 3
(1đ)
Ta có C =
2 2 2
(3x – xy + y – 4) B
C =
2 2 2 2 2
3x – xy + y – 4 ( 3x 4xy 1)
C =
2 2 2 2 2
3x – xy + y – 4 3x 4xy 1
C =
2 2 2
6x + y – 5xy – 3
0,5
a) 0,5 điểm
Thu gọn f(x) = 2x
5
– x
3
+ 4x
2
– 3 0,5
b) 0,5 điểm
Bài 4
(2đ)
Thay x = -1 vào đa thức f(x) ta được:
f(-1) = 2.(-1)
5
– (-1)
3
+ 4.(-1)
2
–3
f(-1) = 2.(-1) – (-1) + 4.1 –3
0,25
f(-1) = –2 +1 + 4 –3
f(-1) = 0.
Vậy x = -1 là nghiệm của đa thức f(x) 0,25
c) 0,5 điểm
h(x) = f(x) – g(x)
h(x) = (2x
5
– x
3
+ 4x
2
– 3) – (2x
5
– x
3
+ 3x
2
– 2x – 6)
0,25
h(x) = 2x
5
– x
3
+ 4x
2
– 3 –2x
5
+ x
3
–3x
2
+ 2x + 6
h(x) = x
2
+ 2x + 3
0,25
d) 0,5 điểm
Ta có: h(x) =
2
x + 2x 3
h(x) =
2
(x + x) ( 1) 2
x
h(x) =
x.(x+ 1) ( 1) 2
x
h(x) =
2
(x+ 1) 2
0,25
Ta thấy
2
(x + 1) 0
với mọi x
R
Suy ra
2
(x + 1) 2
> 0 với mọi x
R
Do đó h(x) không có nghiệm trong R.
0,25
Vẽ hình 0,5 điểm
Vẽ được hình 1
0,5
a) 1 điểm
Xét CAD và CED có:
Cạnh CD chung
ACD ECD
(CD là phân giác của góc ACB)
CA=CE (gt)
Suy ra: CAD = CED (c.g.c)
0,5
Do vậy
0
CAD CED 90
DE BC
0,25
0,25
Bài 5
(4đ)
b) 0,5 điểm
B
K
D
H
M
E
A
C
Hình 2
M
B
D
E
A
C
Hình 1
Xét CAB và CEM có:
CA=CE (gt)
ACB
là góc chung
0
CAB CEM 90
Suy ra: CAB = CEM (g.c.g )
0,25
Do đó AB = EM 0,25
c) 1 điểm
Vì CA=CE (gt) nên CAE cân tại C.
Do đó CD là phân giác góc ACE đồng thời cũng là đường trung
trực của AE
CD AE
(1)
0,25
Mặt khác, theo câu b ta có: CAB = CEM
CB CM
Suy ra CBM cân tại C
0,25
Do đó CD là phân giác góc BCM đồng thời cũng là đường trung
trực của MB
CD MB
(2)
0,25
Từ (1) và (2) suy ra AE//MB (cùng vuông góc với CD) 0,25
d) 1,0 điểm
Kẻ
EK AB (K AB)
Ta có AH//DE (cùng vuông góc với BC)
nên
HAE DEA
(3) (cặp góc so le trong)
Lại có CAD = CED (câu a)
DA DE
Do vậy ADE cân tại D
DAE DEA
(4)
Từ (3) và (4) suy ra
HAE DAE
0,25
AE là tia phân giác của
HAB
EH = EK
0,25
Mặt khác EKB vuông tại K nên EK<EB
0,25
Do đó EH<EB 0,25
Lưu ý: Học sinh làm đúng theo cách khác vẫn cho điểm tối đa.