Sở GD&ĐT Nghệ An Kì thi chọn học sinh giỏi tỉnh
Năm học 2007-2008
Bài 1: (4,0 điểm)
a. Tìm các số tự nhiên có 3 chữ số, biết rằng: số đó là số chẵn, chia hết cho 11 và tổng các chữ số của số đó
cũng chia hết cho 11.
b. Chứng tỏ rằng:
3 3
7 50 7 50 + +
là số tự nhiên.
Bài 2: (4,0 điểm)
a. Giải phơng trình:
2 2
4x 5x 1 3 2 x x 1 9x+ + + = + +
b. Giải hệ phơng trình:
2 2 2
x y z 29
xyz 24
xy 2x 3y 6
y 2
+ + =


=

=

>

Bài 3: (4,0 điểm) Cho a, b là các số thực không âm thoả mãn: a
2
+ b

2
= 1.
a. Chứng minh : 1

a + b


2
b. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
P =
1 2a 1 2b+ + +
Bài 4: (3,0 điểm) Cho 3 số thực x, y, z thoả mãn xyz = 1.
Chứng minh rằng: Nếu x + y + z >
1 1 1
x y z
+ +
thì trong ba số x, y, z có duy nhất một số lớn hơn 1.
Bài 5: (5,0 điểm) Cho đờng tròn tâm O đờng kính AB và dây cung CD (C, D không trùng với A, B). Gọi M là giao điểm
các tiếp tuyến của đờng tròn tại C, D; N là giao điểm các dây cung AC, BD. Đờng thẳng qua N vuông góc với NO cắt
AD, BC lần lợt tại E, F. Chứng minh:
a. MN vuông góc với AB.
b. NE = NF.
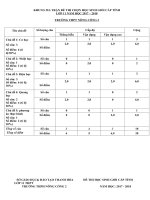
UBND TỉNH Thừa Thiên Huế kỳ thi chọn học sinh giỏi tỉnh
Sở Giáo dục và đào tạo lớp 9 thCS - năm học 2008 - 2009
Môn : Toán
Bài 1: (4,0 điểm)
1. Rút gọn biểu thức:
2 4 5 21 80
10 2
A

+ +
=

2. Giải phơng trình:
2 2
6 18 0x x x x + =
Bài 2: (3,0 điểm)
Cho phơng trình
( ) ( )
3 2
1 3 1 4 1 0 (1)m x m x x m+ + + =
(
m
là tham số).
1. Biến đổi phơng trình (1) về dạng phơng trình tích.
2. Với giá trị nào của
m
thì phơng trình (1) có ba nghiệm phân biệt, trong đó có 2 nghiệm âm.
Bài 3: (4,0 điểm)
1. Chứng minh rằng với hai số thực bất kì
,a b
ta luôn có:
2
2
a b
ab
+


ữ


.
Dấu đẳng thức xảy ra khi nào ?
2. Cho ba số thực
, ,a b c
không âm sao cho
1a b c
+ + =
.
Chứng minh:
16b c abc
+
. Dấu đẳng thức xảy ra khi nào ?
3. Với giá trị nào của góc nhọn

thì biểu thức
6 6
sin cosP

= +
có giá trị bé nhất ? Cho biết giá trị bé nhất
đó.
Bài 4: (6,0 điểm)
1. Cho tam giác ABC vuông tại A. Đờng tròn nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA và AB lần lợt
tại D, E và F. Đặt
, ,x DB y DC z AE= = =
.
a. Tìm hệ thức giữa
,x y
và

z
.
b. Chứng minh rằng:
2AB AC DB DCì = ì
.
2. Cho tam giác ABC cân tại A,
BC a
=
. Hai điểm M và N lần lợt trên AC và AB sao cho:
2 , 2AM MC AN NB= =
và hai đoạn BM và CN vuông góc với nhau. Tính diện tích tam giác ABC theo
a
.
Bài 5: (3,0 điểm)
1. Một đoàn học sinh đi cắm trại bằng ô tô. Nếu mỗi ô tô chở 22 ngời thì còn thừa một ngời. Nếu bớt đi một ô tô
thì có thể phân phối đều tất cả các học sinh lên các ô tô còn lại. Hỏi có bao nhiêu học sinh đi cắm trại và có
bao nhiêu ô tô ? Biết rằng mỗi ô tô chỉ chở không quá 30 ngời.
2. Một tấm bìa hình chữ nhật có kích thớc
1 5ì
. Hãy cắt tấm bìa thành các mảnh để ráp lại thành một hình
vuông.
Giải thích.
B i Cõu Nội dung Điểm
1 (4 điểm)
1.1
(2 đ)
2 4 5 21 80
10 2
A
+ +

=

( )
2
21 80 1 4 5 2 5 1 2 5+ = + + = +
5 21 80 6 2 5 1 5+ + = + = +
( )
2
5 1
2 3 5 6 2 5
1
2( 5 1) 5 1 5 1
A


= = = =

0,5
0,5
1,0
1.2
(2 đ)
2 2
6 18 0x x x x + =
.
Điều kiện để phơng trình có nghĩa:
2
6 0x x
Đặt
( ) ( )

2 2 2
6 0 18 12 0t x x t x x t t= =
Khi đó phơng trình đã cho trở thành:
( )
2
12 0 0 3 ( 4 0t t t t t+ = = = <
loại)
2 2
1 2
1 61 1 61
3 6 9 0 15 0 ;
2 2
t x x x x x x
+
= = > = = =
Vậy phơng trình đã cho có hai nghiệm:
1,2
1 61
2
x

=
0,25
0,5
0,5
0,5
0,25
2 (3 điểm)
2.1
( ) ( )

3 2
1 3 1 4 1 0 (1)m x m x x m+ + + =
( ) ( )
3 2 2
1 1 4 4 1 0m x m x mx x m + + + + =
( ) ( )
( )
( )
2 2
1 1 4 1 1 0m x x m x x + + =
( ) ( )
2
1 1 4 4 1 0x m x mx m

+ + + =

0,5
0,5
0,25
2.2 Ta có:

( ) ( )
( )
2
2
1 1 4 4 1 0
1 ( )
( ) 1 4 4 1 0 ( )
x m x mx m
x a

g x m x mx m b

+ + + =

=



= + + + =

0,5
Để phơng trình (1) có ba nghiệm phân biệt thì phơng trình (b) phải có hai nghiệm
phân biệt khác 1, tơng đơng với:
1
1
1 1
' 1 3 0 1, 0,
3 3
(1) 0
9 0
m
m
m m m m m
g
m







= > < <







(*)
Với điều kiện (*), phơng trình (1) có 3 nghiệm phân biệt, trong đó có một nghiệm
x = 1 > 0 và hai nghiệm còn lại x
1
và x
2
(x
1
< x
2
) là nghiệm của (b). Do đó để (1)
có 3 nghiệm phân biệt trong đó có hai nghiệm âm thì x
1
< x
2
<0, tơng đơng với:
1 2
1 2
4 1
1
0

1
1
1
1
4
4
4
1 0
0
1
m
P x x
m hay m
m
m hay m
m
m hay m
S x x
m


= = >


< >

+
< >




< >
= + = <


+

(**).
Kết hợp (*) và (**) ta có: Để phơng trình (1) có 3 nghiệm phân biệt, trong đó có
hai nghiệm âm thì cần và đủ là:
1 1
1
4 3
m hay m< < <
0,25
0,50
0,25
0,25
3 (4,0 điểm)
3.1 Ta có:
2
2 2 2 2
2 2
2 4 4
a b a ab b a ab b
ab ab
+ + + +

= =
ữ


( )
2
0, ,
4
a b
a b

= R
Vậy:
( )
2
2
, , 4 , ,
2
a b
ab a b a b ab a b
+

+
ữ

R R
Dấu đẳng thức xảy ra khi
a b
=
0,25
0,25
0,25
0,25

Theo kết quả câu 3.1, ta có:
( ) ( ) ( )
2 2
4a b c a b c a b c

+ + = + + +

mà
1a b c
+ + =
(giả thiết)
nên:
( ) ( )
2
1 4 4a b c b c a b c + + +
(vì a, b, c không âm nên b + c không
âm)
Nhng:
( )
2
4b c bc+
(không âm)
Suy ra:
16b c abc
+
.
Dấu đẳng thức xảy ra khi:
1 1
,
4 2

a b c
b c a
b c
= +

= = =

=

0,25
0,25
0,25
0,25
0,50
3.2 Ta có:
( ) ( )
3 3
6 6 2 2
sin cos sin sP co

= + = +
( )
2 2 4 2 2 4
sin cos sin sin cos cosP


= + +

( )
2

2 2 2 2 2 2
sin cos 3sin cos 1 3sin cosP

= + =
áp dụng kết quả câu 3.1, ta có:
( )
2
2 2 2 2 2 2 2 2
1
sin cos 4sin cos 1 4sin cos sin cos
4

+
Suy ra:
2 2
3 1
1 3sin cos 1
4 4
P

= =
Do đó:
min
1
4
P =
khi và chỉ khi:
2 2
sin cos sin cos


= =
(vì

là góc
nhọn)
0
sin
1 1 45
cos
tg



= = =
0,25
0,25
0,25
0,25
0,5
4 (6,0 điểm)
4.1.a + Ta có: BD = BF, CD = CE và
AE = AF (Tính chất của hai
tiếp tuyến cắt nhau).
Do đó:
, ,BC x y AC y z
AB x z
= + = +
= +
Theo định lí Pytago:
2 2 2

BC AB AC= +
( ) ( ) ( )
2 2 2
x y x z y z + = + + +
( ) ( )
2
2 2 2xy z x y z xy z x y z = + + = + +
(a)
0,5
0,5
0,5
4.1.b Gọi
r
là bán kính, I là tâm đờng tròn nội tiếp tam giác ABC.
Ta có:
( )
1 1 1 1
2 2 2 2
ABC
S AB AC BC r CA r AB r x y z r

= ì = ì + ì + ì = + +
(b)
Tứ giác AEIF có 3 góc vuông, nên là hình chữ nhật.
Nhng AE = AF (cm trên), nên AEIF là hình vuông,
Do đó:
z EI r= =
(c)
Từ (a), (b), (c) suy ra:
2 2AB AC xy AB AC DB DCì = ì = ì

0,5
0,5
0,5
4.2
+ Theo giả thiết:
2AM MC
=
và
2AN NC
=
Suy ra:

2 2
//
3 3
AM AN MN AM
MN BC
AC AB BC AC
= = = =
.
+ Gọi E là giao điểm của BM và CN, theo định lí Ta-lét, ta có:
2
3
EM EN MN
EB EC BC
= = =
.
Gọi BK là đờng cao hạ từ B của tam giác ABC, ta có:
1
2

3 3
1
2
ABC
ABC BCM
BCM
AC BK
S
AC
S S
S CM
CM BK
ì
= = = =
ì
0,5
0,5
1,0
2
3 5 5
5 3 12
BEC
BMC BEC
BMC
S
BE a
S S
S BM
= = = =
Vậy:

2
5
4
ABC
a
S =
0,5
0,5
5 (3,0 điểm)
5.1
+ Gọi số ô tô lúc đầu là
x
( x nguyên và x

2)
Số học sinh đi cắm trại là: 22x + 1.
+ Theo giả thiết: Nếu số xe là
1x
thì số học sinh phân phối đều cho tất cả các
xe, mỗi xe chở số học sinh là y (y là số nguyên và 0 < y

30).
+ Do đó ta có phơng trình:
( )
22 1 23
1 22 1 22
1 1
x
x y x y
x x

+
= + = = +

0,25
0,25
0,5
+ Vì x và y đều là số nguyên dơng, nên
1x
phải là ớc số của 23.
Mà 23 nguyên tố, nên:
1 1 2x x
= =
hoặc
1 23 24x x
= =
Nếu
2x
=
thì
22 23 45 30y = + = >
(trái giả thiết)
Nếu
24x
=
thì
22 1 23y = + =
< 30 (thỏa điều kiện bài toán).
+ Vậy số ô tô là: 24 và tổng số học sinh đi cắm trại là:

22 24 1 23 23 529

ì + = ì =
học sinh.
0,25
0,25
0,25
0,25
5.2
+ Tấm bìa hình chữ nhật
1 5
ì
có diện tích là 5
(đvdt).
Để cắt hình chữ nhật thành các mảnh ráp
thành hình vuông, thì cạnh của hình vuông
bằng
5
, bằng độ dài cạnh huyền của tam
giác vuông có hai cạnh góc vuông có kích thớc
là 1 và 2 có diện tích bằng 1 (đvdt).
+ Do đó nếu cắt hình chữ nhật
1 5
ì
theo đờng chéo của 2
hình chữ nhật AEFD và GBCH, và cắt theo 2 đờng EF và GH xong ráp lại thì đ-
ợc hình vuông MNPQ nh hình bên.
1,0
S GIO DC V O TO THI CHN HC SINH GII CP TNH
BC GIANG NM HC 2011-2012
MễN THI:TON LP 9
Cõu 1(5,0 im ):

1. Tớnh giỏ tr ca biu thc sau :
1 4 1 4
1 1 4 1 1 4
x x
A
x x
+
= +
+ +
,bit
2
9
x =
.
2. Tỡm cỏc giỏ tr ca tham s m phng trỡnh (m+1)x
2
(2m+1)x+m-1 =0 cú hai nghim phõn bit tha món
x
1
2
+ x
2
2
-2009x
1
x
2
=2012
Cõu 2(4,0 im ):
1. Gii phng trỡnh :

2
(2 2 4 1)(2 3 4 9 2) 7x x x x x+ + + + + + =
.
2. Gii h phng trỡnh sau :
2 4 2
2 4 2
2 4 2
x y z
y z x
z x y

+ =


+ =


+ =


Cõu 3(4,0 im):
1. Tỡm giỏ tr ln nht,giỏ tr nh nht ca x bit x v y l hai s tha món ng thc y
2
=3(xy+y-x-x
2
).
2. Tỡm cỏc s nguyờn k biu thc k
4
-8k
3

+23k
2
-26k+10 l s chớnh phng.
Cõu 4 (6,0 im ):
Cho ng trũn (O) ng kớnh AB.Trờn on thng AO ly im H bt kỡ khụng trựng vi A v O,k ng
thng d vuụng gúc vi AB ti H,trờn d ly im C nm ngoi ng trũn,t C k hai tip tuyn CM v CN vi ng
trũn (O) vi M, N l cỏc tip im ,(M thuc na mt phng b d cú cha im A).Gi P v Q ln lt l giao im
ca CM,CN vi ng thng AB.
1. Chng minh HC l tia phõn giỏc ca gúc MHN
a s dng x,y v z tha món x+y+z=6.Chng minh rng :
x
2
+y
2
+z
2
xy-yz-xz +xyz 8.
THI HC SINH GII CP TNH
NM HC 2011 2012
MễN THI: TON LP 9 THCS
Cõu 1.(4,0 im)
1. Rỳt gn biu thc:
2 3 2 3
2 2 3 2 2 3
+
+
+ +
2. Cho hai s dng
,a b
tha món

5a b+ =
. Tỡm giỏ tr nh nht ca biu thc

1 1
P
a b
= +
Cõu 2.(5,0 im)
1. Gii phng trỡnh:
4
20 4x x+ =

2. Gii h phng trỡnh:





=+
=++
xyxyyx
xyyx
5224412
672)1(3)4(
Cõu 3.(3,0 im)
Tìm tất cả các số nguyên
n
sao cho
( 2010)( 2011)( 2012)A n n n
= − − −

là một số chính phương.
Câu 4.(6,0 điểm)
Cho tam giác ABC có
·
0
60 ; ;ABC BC a AB c= = =
(
,a c
là hai độ dài cho trước). Hình chữ nhật
MNPQ có đỉnh M nằm trên cạnh AB, N nằm trên cạnh AC, P và Q nằm trên cạnh BC được gọi là hình chữ nhật nội
tiếp trong tam giác ABC.
1. Tìm vị trí của M trên cạnh AB để hình chữ nhật MNPQ có diện tích lớn nhất. Tính diện tích lớn nhất đó.
2. Dựng hình vuông EFGH (E nằm trên cạnh AB, F nằm trên cạnh AC, G và H nằm trên cạnh BC ) nội tiếp
trong tam giác ABC bằng thước kẻ và com-pa. Tính diện tích của hình vuông đó.
Câu 5.(2,0 điểm)
Chứng minh rằng luôn tồn tại số nguyên dương tận cùng là 2012 chia hết cho 2011.
SỞ GIÁO DỤC – ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 THCS
BÌNH ĐỊNH NĂM HỌC : 2011 – 2012
Bài 1: ( 4,0 điểm )
a) Rút gọn biểu thức sau: A =
8 15 8 15
2 2
+ −
+
b) Giải phương trình :
3
2
2
16 0
16

x
x
x
+ − =
−
Bài 2: ( 4, 0 điểm)
a) Chứng minh rằng n
3
– n chia hết cho 24 với mọi số tự nhiên n lẻ.
b) Cho a, b, c là các số thực dương thõa điều kiện :
a
2
+ b
2
+ c
2
= (a –b)
2
+ (b- c)
2
+ ( c – a)
2

Chứng minh rằng nếu c
≥
a và c
≥
b thì c
≥
a + b

Bài 3: ( 3, 0 điểm )
Cho phương trình x
2
+(m – 1)x – 6 = 0. Tìm m để phương trình có hai nghiệm phân biệt x
1
và x
2
sao cho biểu
thức A = (x
1
2
– 9)(x
2
2
– 4) đạt giá trị lớn nhất.
Bài 4: (6, 0 điểm)
1) Cho tam giác ABC cân tại A có BAC = 20
0
; AB = AC = b và BC = a .
Chứng minh rằng : a
3
+ b
3
= 3ab
2
.
2) Cho hai điểm A, B thuộc đường tròn (O) (AB không đi qua O) và có hai điểm C, D di động trên cung lớn
AB sao cho AD song song BC ( C, D khác A, B và AD > BC ). Gọi M là giao điểm của BD và AC . Hai tiếp tuyến của
đường tròn (O) tại A và D cắt nhau tại điểm I.
a) Chứng minh ba điểm I, O, M thẳng hàng.

b) Chứng minh bán kính đường tròn ngoại tiếp tam giác MCD không đổi.
Bài 5: ( 3,0 điểm )
Cho x, y là các số thực dương thõa mãn xy = 1 .
Chứng minh rằng : (x + y + 1)(x
2
+ y
2
) +
4
x y+

≥
8
HƯỚNG DẪN GIẢI:
Bài 1: ( 4,0 điểm )
a) A =
8 15 8 15
2 2
+ −
+
* Cách 1: A
2
=
2
8 15 8 15
2 2
 
+ −
 ÷
+

 ÷
 
=
8 15
2
+
+
8 15
2
−
+ 2
8 15 8 15
.
2 2
+ −
= 8 + 2
49
4
= 8 + 7 = 15
Vì A > 0 nên A =
15
* Cách 2: A =
8 15 8 15
2 2
+ −
+
=
16 2 15 16 2 15
4 4
+ −

+

=
2 2
( 15 1) ( 15 1)
4 4
+ −
+
=
15 1 15 1
2 2
+ −
+
=
15
b)
3
2
2
16 0
16
x
x
x
+ − =
−
. ĐK : 16 – x
2
> 0
⇔

- 4 < x < 4
Đặt y =
2
16 x−
> 0
⇒
x
2
– 16 = - y
2
. Ta có :

3
x
y
- y
2
= 0
⇒
x
3
– y
3
= 0
⇔
(x – y)(x
2
– xy + y
2
) = 0

⇔
x – y = 0 ( vì x
2
– xy + y
2
> 0 )
⇔
x = y .
2
16 x−
= x . Với x > 0 thì
2
16 x−
= x
⇔
16 – x
2
= x
2

⇔
2x
2
= 16
⇔
/x/ =
8

⇔
x =

±
8
Kết hơp các điều kiện x > 0 và - 4 < x < 4 , ta có x =
8
thõa mãn .
Phương trình có một nghiệm x =
8
.
Bài 2: ( 4, 0 điểm)
a) n
3
– n = n(n
2
– 1) = n(n – 1)(n + 1).
Với n lẻ thì n – 1 và n + 1 là hai số chẵn liên tiếp nên có một số chia hết cho 2 , số còn lại chia hết cho 4. Do đó tích
(n – 1)(n + 1) chia hết cho 8.
Mặt khác, tích n(n – 1)(n + 1) là tích của ba số tự nhiên liên tiếp nên chia hết cho 3.
Mà (3; 8) = 1 nên n(n – 1)(n + 1) chia hết cho 3.8 = 24.
Vậy : n
3
– n chia hết cho 24 với n lẻ.
b) Từ điều kiện : a
2
+ b
2
+ c
2
= (a –b)
2
+ (b- c)

2
+ ( c – a)
2

Suy ra : a
2
+ b
2
+ c
2
= 2(a
2
+ b
2
+ c
2
) – 2(ab + bc + ca)

⇔
a
2
+ b
2
+ c
2
= 2(ab + bc + ca)
* Cách 1 : Nếu c
≥
a và c
≥

b thì a
2
+ b
2
+ c
2
= 2ab + 2bc + 2ca
≥
2ab + 2b
2
+ 2a
2


⇒
c
2

≥
( a + b)
2

⇒
c
≥
a + b ( vì a, b, c > 0 )
* Cách 2 : Từ a
2
+ b
2

+ c
2
= 2ab + 2bc + 2ca
⇒
a
2
+ b
2
+ c
2
- 2ab - 2bc - 2ca = 0

⇒
( a – b + c )
2
= 4ca . Nếu c
≥
a thì ( a – b + c )
2
= 4ca
≥
4a
2

⇔
( a – b + c )
2
- 4a
2


≥
0
⇔
(a – b + c – 2a )(a – b + c + 2a )
≥
0
⇔
( c – a – b )(3a – b + c)
≥
0
Vì a > 0 và nếu c
≥
b thì 3a – b + c > 0 .
⇒
c – a – b
≥
0
⇒
c
≥
a + b .
Bài 3: ( 3, 0 điểm )
Phương trình x
2
+(m – 1)x – 6 = 0 có
∆
= ( m – 1)
2
+ 24 > 0 với mọi m nên luôn có hai nghiệm phân biệt x
1


và x
2
.
Áp dụng định lý Vi-et : x
1
+ x
2
= 1 – m ; x
1
.x
2
= - 6
A = (x
1
2
– 9)(x
2
2
– 4) = (x
1
.x
2
)
2
– 4x
1
2
– 9x
2

2
+ 36 = 72 - 4x
1
2
– 9x
2
2
= – (4x
1
2
+ 9x
2
2
+ 12 x
1
.x
2
)
= – ( 2x
1
+ 3x
2
)
2

≤
0
A = 0
⇔


( )
( )
( )
1 2
1 2
1 2
2 3 0 1
. 6 2
1 3
x x
x x
x x m

+ =

= −


+ = −

.
Từ (2)
⇒
x
1
=
2
6
x
−

, thay vào (1) có :
2
12
x
−
+ 3x
2
= 0
⇒
x
2
=
±
2
- Với x
2
= 2
⇒
x
1
= - 3 . Thay vào (3) có : 1 – m = - 1
⇒
m = 2
- Với x
2
= - 2
⇒
x
1
= 3 . Thay vào (3) có : 1 – m = 1

⇒
m = 0
- Vậy : m
∈
{ 0 ; 2 }
Bài 4: (6, 0 điểm)
1) Cho tam giác ABC cân tại A có BAC = 20
0
; AB = AC = b và BC = a .
Chứng minh rằng : a
3
+ b
3
= 3ab
2
.
B
C
A
D
E
∆
ABC cân tại A có góc BAC = 20
0
nên ABC = ACB = 80
0
Trên cạnh AC lấy D sao cho ABD = 60
0
, khi đó DBC = 20
0

nên BDC = 80
0
⇒

∆
BDC cân tại B
⇒
BD = BC = a .
∆
BDC
∆
ABC ( g – g)
⇒

DC BC
BC AC
=

⇒
DC =
2
a
b
⇒
AD = b -
2
a
b
∆
BDE vuông có EBD = 60

0
nên BE =
1
2
BD =
1
2
a và DE = BD
3
2
= a.
3
2
;
AE = b -
1
2
a.
Áp dung định lý Pi-ta-go trong tg vuông ADE có :
AD
2
= AE
2
+ DE
2

⇔
(b -
2
a

b
)
2
= (b -
1
2
a)
2
+ (a.
3
2
)
2

⇔
b
2
- 2a
2
+
4
2
a
b
= b
2
- ab +
2
4
a

+
2
3
4
a

⇔

4
2
a
b
= 3a
2
–ab
⇒
a
4
= 3a
2
b
2
- ab
3

⇔
a
4
+ ab
3

= 3a
2
b
2

⇔
a
3
+ b
3
= 3ab
2
.
2) Cho hai điểm A, B thuộc đường tròn (O) (AB không đi qua O) và có hai điểm C, D di động trên cung lớn
AB sao cho AD song song BC ( C, D khác A, B và AD > BC ). Gọi M là giao điểm của BD và AC . Hai tiếp tuyến của
đường tròn (O) tại A và D cắt nhau tại điểm I.
a) Chứng minh ba điểm I, O, M thẳng hàng.
b) Chứng minh bán kính đường tròn ngoại tiếp tam giác MCD không đổi.
E'
E
M
O
I
A
D
B
C
a) AD // BC
⇒
AB = CD

⇒
DAC = ADB
⇒
MA = MD .
Lại có : OA = OD = R nên MO là đường trung trực của AD (1)
Mặt khác : IA và ID là hai tiếp tuyến của (O) nên OI là đường trung trực của
AD (2)
Từ (1) và (2)
⇒
I, O, M thẳng hàng.
b) Tứ giác CMOD có : CMD = 2. MAD ( góc ngoài của tg cân)
COD = 2. MAD ( góc ở tâm và góc nội tiếp)
⇒
CMD = COD
Do đó tứ giác CMOD nội tiếp.
Tương tự tứ giác BMOA nội tiếp
Qua M vẽ đường thẳng d song song với AD cắt đường tròn ngoại tiếp tứ giác
BMOA tại E , cắt đường tròn ngoại tiếp tứ giác CMOD tại E’.
Do A đối xứng D qua đường thẳng OM, C đối xứng B qua OM nên đường
tròn ngoại tiếp tứ giác CMOD đối xứng với đường tròn ngoại tiếp tứ giác
BMOA qua OM.
OM
⊥
ME nên OE là đường kính của đường tròn (BMOA)
A, O, B cố định nên E cố định
⇒
OE không đổi
⇒
Đường tròn ngoại tiếp
∆

MCD có bán kính không đổi.
Bài 5: ( 3,0 điểm )
Cho x, y là các số thực dương thõa mãn xy = 1 .
Chứng minh rằng : (x + y + 1)(x
2
+ y
2
) +
4
x y+

≥
8
Ta có : (x + y + 1)(x
2
+ y
2
) +
4
x y+
= (x + y + 1)(x
2
+ y
2
) - ( x + y) + ( x + y ) +
4
x y+

= ( x + y )( x
2

+ y
2
) + (x
2
+ y
2
) - ( x + y) + ( x + y ) +
4
x y+

= ( x + y ) (x
2
+ y
2
– 1) + (x
2
+ y
2
) + ( x + y ) +
4
x y+

Áp dụng bất đẳng thức Cauchy cho hai số dương :
x + y
≥
2
xy
= 2 ( do xy = 1 ) . Dấu “ = “ xảy ra
⇔
x = y = 1

x
2
+ y
2

≥
2xy = 2 . Dấu “ = “ xảy ra
⇔
x = y = 1
( x + y ) +
4
x y+

≥
4 . Dấu “ = “ xảy ra
⇔
(x + y)
2
= 4
⇒
x = y = 1.
Do đó : (x + y + 1)(x
2
+ y
2
) +
4
x y+

≥

2.(2 – 1) + 2 + 4 = 8
Dấu “ = “ xảy ra
⇔
x = y = 1
SỞ GIÁO DỤC BÌNH ĐỊNH KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 THCS
BÌNH ĐỊNH NĂM HỌC 2012 – 2013
Bài 1: (5 điểm)
a) Tính giá trị của biểu thức :
1 1
A
2 2 3
2 2 3
= +
- -
+ +
b) Giải phương trình :
2 2
x y 11
x xy y 3 4 2
ì
ï
+ =
ï
í
ï
+ + = +
ï
î
Bài 2: (4,0 điểm)
a) Chứng minh rằng trong 8 số tự nhiên có ba chữ số bất kỳ, bao giờ cũng tìm được hai số mà khi viết chúng

liền nhau ta được một số có 6 chữ số chia hết cho 7.
b) Cho hai số thực x, y dương thõa mãn điều kiện x
2
+ y
2
– xy = 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức : P = x
2
+ y
2
.
Bài 3: ( 4 điểm)
Trong mặt phẳng tọa độ Oxy, cho parabol (P) : y = - x
2
và đường thẳng (d) có phương trình
y = mx – 1 ( m là tham số)
a) Chứng minh rằng với mọi m đường thảng (d) luôn cắt Parabol (P) tại hai điểm phân biết A và B.
b) Gọi hoành độ giao điểm của A và B lần lượt là x
1
; x
2
. Chứng minh rằng : | x
1
– x
2
|
³
2.
Bài 4: (3,0 điểm)
Cho

Δ
ABC cân tại A nội tiếp đường tròn (O). Gọi D là trung điểm của cạnh AB và E là trọng tâm của
Δ
ACD. Chứng minh rằng : OE
^
CD.
Bài 5: ( 4 điểm)
Cho đường tròn (O;R) có đường kính AB cố định và đường kính CD thay đối (CD không trùng với AB). Vẽ
tiếp tuyến (d) với đường tròn (O;R) tại B. Các đường thẳng AC, AD lần lượt cắt đường thẳng (d) tại P và Q.
a) Chứng minh tứ giác CPQD là một tứ giác nội tiếp.
b) Gọi E là tâm của đường tròn ngoại tiếp
Δ
CDP. Chứng minh rằng khi đường kính CD thay đổi (CD không
trùng với AB) thì E di chuyển trên một đường thẳng cố định.
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI CHỌN HỌC SINH GIỎI THCS
TỈNH BÌNH DƯƠNG Năm học: 2011-2012
Môn: TOÁN
Câu 1: (4 điểm):
a) Chứng minh rằng a
3
– a chia hết cho 6 với mọi số nguyên a .
b) Cho n số nguyên a
1
, a
2
, , a
n
có tổng a
1
+ a

2
+ + a
n
chia hết cho 6 ( n là số nguyên dương). Chứng minh
rằng a
1
3
+ a
2
3

+ + a
n
3
chia hết cho 6 .
Câu 2: (4 điểm):Giải phương trình :
2
2
1
1
x
x
x
 
+ =
 ÷
+
 
Câu 3: (4 điểm):
Cho hai phương trình ax

2
+ bx + c = 0 (1) và cx
2
+ bx + a = 0 (2) trong đó a > c > 0 .
a) Chứng minh phương trình (1) và (2) cùng có nghiệm hay vô nghiệm .
b) Giải phương trình (1) và (2) có nghiệm tương ứng x
1
, x
2
và x’
1
, x’
2
sao cho x
1
+ x
2
> x’
1
+ x’
2
. Chứng
minh: b > 0 .
c) Giả sử phương trình (1) và (2) cùng vô nghiệm. Chứng minh b < a + c .
Câu 4: (4 điểm):
Cho tam giác ABC có 3 góc nhọn, H là trực tâm của tam giác. Các đường thẳng song song với AB, AC và đi qua
H cắt AC, AB lần lượt tại E, F.
Chứng minh AB + AC > AH + BH + CH .
Câu 5: (4 điểm):
Cho tam giác ABC nội tiếp đường tròn tâm (O). Phân giác góc A của tam giác cắt đường tròn (O) tại M. Kẻ đường

cao AH của tam giác cắt đường tròn (O) tại E, vẽ đường kính AOD.
a) Tứ giác BEDC là hình gì ?
b) Chứng minh AM là phân giác của góc EAD .
Hết
Giải
Câu 1: (4 điểm):
a) Chứng minh rằng a
3
– a chia hết cho 6 với mọi số nguyên a .
a
3
– a = a(a
2
– 1) = (a – 1).a.(a + 1) là 3 số nguyên liên tiếp luôn chia hết cho 2 và 3
⇒
a
3
– a chia hết cho 2.3 = 6 với mọi số nguyên a .
b) Cho n số nguyên a
1
, a
2
, , a
n
có tổng a
1
+ a
2
+ + a
n

chia hết cho 6 ( n là số nguyên dương). Chứng minh
rằng a
1
3
+ a
2
3

+ + a
n
3
chia hết cho 6 .
Câu 2: (4 điểm):
Giải phương trình :đk: x ≠ -1

⇔
1
1
2
)
1
(
1
2
2
2
2
2
=
+

+
+
+
+
−
x
x
x
x
x
x
x

⇔
1
1
.2)
1
(
2
2
=
+
+
+
−
x
x
x
x

x
⇔

2)1
1
(
2
2
=+
+
x
x
⇔

2
2
(1 2) (1 2) 0
(1 2) (1 2) 0
x x
x x

+ − + − =

+ + + + =


Câu 3: (4 điểm):
Cho hai phương trình ax
2
+ bx + c = 0 (1) và cx

2
+ bx + a = 0 (2) trong đó a > c > 0 .
d) Chứng minh phương trình (1) và (2) cùng có nghiệm hay vô nghiệm .
e) Giải phương trình (1) và (2) có nghiệm tương ứng x
1
, x
2
và x’
1
, x’
2
sao cho x
1
+ x
2
> x’
1
+ x’
2
. Chứng
minh: b > 0 .
f) Giả sử phương trình (1) và (2) cùng vô nghiệm. Chứng minh b < a + c .
Câu 4: (4 điểm):
Cho tam giác ABC có 3 góc nhọn, H là trực tâm của tam giác. Các đường thẳng song song với AB, AC và đi qua
H cắt AC, AB lần lượt tại E, F.
Chứng minh AB + AC > AH + BH + CH .
Câu 5: (4 điểm):
Cho tam giác ABC nội tiếp đường tròn tâm (O). Phân giác góc A của tam giác cắt đường tròn (O) tại M. Kẻ đường
cao AH của tam giác cắt đường tròn (O) tại E, vẽ đường kính AOD.
c) Tứ giác BEDC là hình gì ?

d) Chứng minh AM là phân giác của góc EAD .
SỞ GIÁO DỤC VÀ ĐÀO TẠO BÌNH PHƯỚC
KÌ THI CHỌN LỌC HỌC SINH GIỎI LỚP 9 TRUNG HỌC CƠ SỎ
Khóa ngày : tháng năm 2012
Môn thi : TOÁN
Bài 1: Cho hệ phương trình
4 10
4
mx y m
x my
+ = −


+ =

(m là tham số)
a) Giải và biện luận theo m.
b) Với giá trị nào của số nguyên m, hệ có nghiệm (x ; y) với x ; y là các số nguyên dương.
Bài 2 : a) Cho a , b , c là độ dài ba cạnh của một tam giác. Chứng minh rằng :
2 2 2
6
a b c
b c a a c b a b c
+ + ≥
+ − + − + −
b) Chứng minh: với n
∈
N thì: n
2
+ 13n + 62

,
169
Bài 3: Tính giá trị biểu thức : A = (3x
3
+ 8x
2
+ 2)
2010
Với x =
( )
3
5 2 17 5 38
5 14 6 5
+ −
+ −
Bài 4 : Giải các phương trình: x
3
+ 1 = 2
3
2 1x −
Bài 5: Cho nửa đường tròn (O) đường kính AB = 2R . Kẻ hai tiếp tuyến Ax và By của đường tròn (O) và tiếp tuyến
thứ ba tiếp xúc với (O) tại điểm M cắt Ax tại D , By tại E.
a) Chứng minh:
∆
DOE vuông.
b) Chứng minh : AD . BE = R
2

c) Xác định vị trí của M trên nửa đường tròn (O) sao cho diện tích tam giác DOE đạt giá trị nhỏ nhất.

Đề thi HSG lớp 9 tỉnh Bình Phước năm học 2012-2013
ĐỀ THI HSG TỈNH ĐAK NÔNG NĂM HỌC 2012-2013
Bài 1 (3 đ): Rút gọn biểu thức:
3
2
3
3
2
3
4
3
22
3
4
yxyx
yyxx
++
++
với x; y khác 0
Bài 2(3đ): Giải hệ phương trình:
134
33
=−−+ xx
Bài 3:(2đ): Giải hệ phương trình






+=−
+=+
32
12
33
22
abba
abba
Bài 4:(5 đ)
a) Tìm các cặp số nguyên (x;y) thỏa mãn:
02435438518
2422242
=+−++− yyxyxyx
b)Tìm GTNN của hàm số: y=
5252
22
+−+++ xxxx
Bài 5(2đ) Cho ba số dương a,b,c có a+b+c
6≤
. Chứng minh rằng
1+
8
271111111
≥++++++
abcbcacabcba
Bài 6:(5 đ) Cho nửa đường tròn (O) đường kính AB=2R. Gọi I là trung điểm đoạn thẳng OB, M là điểm nằm trên

đường tròn (O). Đường thẳng trung trực d của đoạn OB cắt AM, BM lần lượt tại N, P.
a/ CMR: IN.IP=
4
3
2
R
b/ Gọi E là giao điểm của d với nửa đường tròn. Trong trường hợp M nằm trên cung AE. Tìm vị trí của điểm
M để chu vi tứ giác AMPO đạt giá trị lớn nhất.

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỒNG NAI
ĐỀ THI CHÍNH THỨC
THI CHỌN HỌC SINH GIỎI LỚP 9
NĂM HỌC 2012 – 2013
Môn: Toán
Thời gian làm bài: 150 phút.
Ngày thi: 05/4/2013
(Đề thi này gồm một trang, có năm câu)
Câu 1 ( 4 điểm).
Cho đa thức P(x) = x
3
+ 3ax + 2b, với x là biến số thực, a và b là các số thực cho trước thỏa a
3
+ b
2

≥
0.
Tính giá trị của đa thức P(x) tại x =
3 3

3 2 3 2
a b b a b b+ − − + +
Câu 2 (4 điểm) . Giải hệ phương trình:
2
2
2 1 0
3 1 0
x y
y x y

− + =


+ − + =


(với x
∈¡
và y
∈¡
)
Câu 3. (3,5 điểm).
Cho các số nguyên dương m, n, k thỏa mãn m.n = k
2
và ước chưng lớn nhất của các số m, n, k bằng 1.
Chứng minh rằng m, n là số chính phương.
Câu 4. (4 điểm)
Cho S là tập hợp các số nguyên dương nhỏ hơn 1000.
1) Tính số phần tử của tập hợp S là bội của 3.
2) Tính số phần tử của tập hợp S không là bội của 2 và không là bội của 3.

Câu 5 (4, 5 điểm)
Cho tứ giác HIJK có
·
·
0
90IHK JKH= =
, 0<IH – JK <IJ<IH + JK.
Gọi (I) là đường tròn tâm I và tiếp xúc với đường thẳng HK tại H. Gọi (J) là đường tròn tâm J và tiếp xúc với
đường thẳng HK tại K. Đường tròn (I) cắt đường tròn (J) tại M và N, với hai điểm M và H nằm khác phía đối
với đường thẳng IJ. Gọi d là đường thẳng đi qua điểm M và song song với đường thẳng HK; đường thẳng d
cắt đường tròn (I) tại A (A
≠
M); đường thẳng d cắt đường tròn (J) tại điểm B, với (B
≠
M). Gọi C là giao
điểm của hai đường thẳng MN và HK.
1) Chứng minh HK là đường trung bình tam giác ABC.
2) Chứng minh rằng DH = DK.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NAM
ĐỀ THI CHÍNH THỨC
KỲ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 9 TRUNG HỌC CƠ SỞ NĂM HỌC 2011-2012
Môn thi: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian giao đề
Bài 1. (4,0 điểm) Cho biểu thức
2 2
2 2
2 2
2 2

x x x x x x
A
x x x x x x
− + + +
= −
+ + − +
.
1. Tìm điều kiện của x để biểu thức A xác định.
2. Rút gọn biểu thức A.
3. Tìm x để
2 3A ≤
.
Bài 2. (4,5 điểm)
1. Cho ba số thực a, b, c sao cho phương trình ax
2
+bx+c=0 có 2 nghiệm thuộc đoạn [0;1]. Tìm giá trị lớn nhất
của biểu thức
( )(2 )
( )
a b a b
P
a a b c
− −
=
− +
.
2. Tìm tất cả các nghiệm nguyên của phương trình
2 2
(2 2) 7( 2 1)x y x y y− − = − − −
.

Bài 3. (4,0 điểm)
1. Tìm giá trị nhỏ nhất của biểu thức Q =
2 2
16 8 1 16 24 9x x x x− + + − +
.
2. Giải hệ phương trình
2 2
2 2
8
16
5
12 3 5
2
xy
x y
x y
x x y x x

+ + =

+



+ + + = + +


Bài 4. (5,5 điểm) Cho đường tròn (O; R) đường kính AB, lấy điểm I thuộc đoạn AO sao cho AO = 3.IO. Qua I vẽ dây
cung CD vuông góc với AB, trên đoạn CD lấy điểm K tuỳ ý. Tia AK cắt đường tròn (O) tại điểm thứ hai là M.
1. Chứng minh tứ giác IKMB nội tiếp.

2. Chứng minh rằng tâm F của đường tròn ngoại tiếp tam giác MKC nằm trên một đường thẳng cố định.
3. Khi K di động trên đoạn CD, tính độ dài nhỏ nhất của đoạn DF.
Bài 5. (2,0 điểm) Cho tam giác ABC không cân, nội tiếp đường tròn (O). Đường phân giác trong AD và đường trung
tuyến AM của tam giác ABC cắt đường tròn (O) theo thứ tự tại P và Q ( P, Q khác A). Chứng minh: DP > MQ.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 9 TRUNG HỌC CƠ SỞ NĂM HỌC 2011-2012
Môn thi: TOÁN
ĐÁP ÁN-BIỂU ĐIỂM
(Đáp án biểu điểm này gồm 3 trang)
Câu Nội dung
Câu 1.1
(1,5 đ)
A xác định
2
2 2
2 0
2 0; 2 0
x x
x x x x x x

+ ≥

⇔

+ + ≠ − + ≠


2

2 0 2; 0x x x x+ ≥ ⇔ ≤ − ≥
2 2
2 0; 2 0 0x x x x x x x+ + ≠ − + ≠ ⇔ ≠
Vậy A xác định
2x
⇔ ≤ −
và
0x
>
Câu 1.2
(1,5 đ)
2 2 2 2
2 2
( 2 ) ( 2 )
( 2 )( 2 )
x x x x x x
A
x x x x x x
− + − + +
=
− + + +
2
2
4 2
2 2
2
x x x
A x x
x
− +

= = +
−
Câu 1.3
(1,0 đ)
2 2
2 3 2 2 2 3 2 3 0A x x x x≤ ⇔ + ≤ ⇔ + − ≤
3 1x
⇔ − ≤ ≤
. Kết hợp với ĐK xác định của A thì
2 3 0 1A x≤ ⇔ < ≤
Câu 2.1
(2,5 đ)
Gọi 2 nghiệm của pt là
1 2
,x x
. Theo Viét ta có :
1 2
1 2
b
x x
a
c
x x
a

+ = −





=


2 2
1 2 1 2 1 2 1 2
1 2 1 2 1 2 1 2
(1 )(2 )
(1 )(2 ) : (1 ) 2
1 1
x x x x x x x xb b b c
P
a a a a x x x x x x x x
+ + + + + + +
= − − − + = = +
+ + + + + +
Không mất tính tổng quát giả sử
1 2
x x≤

khi đó từ giả thiết
[ ]
2 2
1 2 1 1 2 2 1 2 1 2
; 0;1 1; 1 0x x x x x x x x x x∈ ⇒ ≤ ≤ ≤ + + + >
Dẫn tới
2 2
1 2 1 2 1 2 1 2
1 2 1 2 1 2 1 2
1
1

1 1
x x x x x x x x
x x x x x x x x
+ + + + + +
≤ =
+ + + + + +
suy ra
3P
≤
P=3 khi
1 2
1x x= =
suy ra
2
b
a c= = −
. Vậy MaxP=3
Câu 2.2
(2,0 đ)

2 2
(2 2) 7( 2 1)x y x y y− − = − − −
(1)

2 2
2(2 2) 7(2 2) 7(2 3 ) 0x y x y y y⇔ − − − − − + + =
(2)
Đặt
2 2t x y= − −
ta có pt:

2 2
7 7(2 3 ) 0t t y y− + + =


2 2
16 56 49 7(16 24 9) 112t t y y⇔ − + + + + =

2 2
(4 7) 7(4 3) 112t y⇔ + + + =
(3)
Từ (3)
2 2
7(4 3) 112 (4 3) 16 4 4 3 4 7 4 1y y y y⇒ + ≤ ⇔ + ≤ ⇔ − ≤ + ≤ ⇔ − ≤ ≤
Vì y nguyên suy ra y chỉ có thể là -1 hoặc 0
Với y = -1 thay vào (1) được pt
2
(2 1) 7x x− =
không có nghiệm x nguyên
Với y = 0 thay vào (1) được pt
2
4( 1) 7( 1)x x− = −
, pt này có một nghiệm nguyên x = 1
Thử lại thấy (x ;y) = (1 ;0) là nghiệm nguyên duy nhất của pt đã cho.
ĐÁP ÁN CHÍNH THỨC
Cách khác : Xét điều kiện có nghiệm của pt bậc 2 theo ẩn x hoặc y
Câu 3.1
(2,0đ)
Q=
2 2 2 2
16 8 1 16 24 9 (4 1) (3 4 ) 4 1 3 4x x x x x x x x+ + + − + = + + − = + + −

4 1 3 4 4x x≥ + + − =
Q = 4
1 3
(4 1)(3 4 ) 0
4 4
x x x⇔ + − ≥ ⇔ − ≤ ≤
Vậy GTNN của Q là 4 khi
1 3
4 4
x− ≤ ≤
Câu 3.2
(2,0 đ)
Giải hệ
2 2
2 2
8
16 (1)
5
12 3 5 (2)
2
xy
x y
x y
x x y x x

+ + =

+




+ + + = + +


ĐK:
0x y+ ≥
(1)
⇔

+ + − + = +x y x y xy xy x y
2
( )(( ) 2 ) 8 16( )

⇔

+ + − − + − =x y x y xy x y
2
( )(( ) 16) 2 ( 4) 0
⇔ + − + + + =x y x y x y
2 2
( 4)( 4( )) 0

⇔

+ − =x y 4 0
(vì
x y 0+ >
nên
+ + + >x y x y
2 2

4( ) 0
)
Thay x+y=4 vào pt thứ 2 ta được :
2 2
12 5 3 5x x x+ + = + +
2 2
12 5 3 5x x x⇔ + − + = −
(*)
Nhận xét: VT>0
5
0
3
VP x⇒ > ⇒ >
,
(*)
2 2
12 4 3 6 5 3x x x⇔ + − = − + + −

( ) ( )
2 2
2 2 2 2
2 2
4 4 2 2
3 2 2 3 0
12 4 5 3 12 4 5 3
2
2 2
3 0 (**)
12 4 5 3
x x x x

x x
x x x x
x
x x
x x
 
− − + +
⇔ = − + ⇔ − − − =
 ÷
+ + + + + + + +
 
=


⇔
+ +

− − =

+ + + +


(**) vô nghiệm Vì
5
3
x >

2 0x⇒ + >
, mà
2 2

2 2
2 2
2 2
12 4 5 3
12 4 5 3
2 2 5
3 0,
3
12 4 5 3
x x
x x
x x
x x
x
x x
+ +
+ + > + + ⇒ <
+ + + +
+ +
⇒ − − < ∀ >
+ + + +
Vậy (*) có nghiệm x=2 suy ra hệ đã cho có một nghiệm duy nhất (x;y)=(2;2)
Câu 4

Câu 4.1 1. c/m tứ giác IKMB nội tiếp
(1,0 đ)
Ta có
·
0
90KMB =

( vì chắn nửa đường tròn (O)
Lại có
·
0
90KIB =
(gt) nên tứ giác IKMB nội tiếp (vì có 2 góc đối cùng vuông)
Câu 4.2
(2,5 đ)
2. c/m tâm F của (CKM) thuộc một đường cố định
Vẽ đường kính CE của (CKM) , ta có KE // AB ( vì cùng
⊥
CD)
·
·
MKE MAB⇒ =
(đ/vị)
Lại có
· ·
MKE MCE=
(cùng chắn cung
¼
ME
của (F) )

·
·
MAB MCB=
(cùng chắn cung
»
MB

của (O) )
Suy ra
·
·
MCE MCB= ⇒
C, E, B thẳng hàng
⇒
C, F, B thẳng hàng
Suy ra F thuộc đường thẳng CB cố định
Câu 4.3
(2,0 đ)
3. Tính độ dài ngắn nhất của DF
Kẻ DH
⊥
CB tại H
⇒
DH không đổi
Ta có DF
≥
DH nên DF ngắn nhất bằng DH
Ta có
2
2 2 2
2 2 4 2
9 3 3
R R R
CI CO IO R CD= − = − = ⇒ =
2
2
4 8 2 6

. .2
3 3 3
R R R
CB BI BA R CB= = = ⇒ =
Lại có DH.CB=BI.CD ( bằng nửa S
∆
CBD
)
.BI CD
DH
CB
⇒ =
DH
4 4 2
.
8 3
3 3
9
2 6
3
R R
R
R
= =
. Vậy DF ngắn nhất bằng
8 3
9
R
Câu 5
(2,0 đ)


Tam giác ABC không cân nên
M D P Q≠ ⇒ ≠
Lấy điểm I đối xứng với D qua M , gọi K là trung điểm PI.
Ta có
·
·
PAB PAC PM BC PID= ⇒ ⊥ ⇒ ∆
cân tại P
Mặt khác
·
¼
»
»
·
·
1 1
( )
2 2
MQP sd ABP sd AB sdCP CDP DIP= = + = =
Do đó tứ giác PMIQ nội tiếp .Từ
·
0
90PMI =
ta có
·
0
90PQI =
Vì thế PD=PI=PK+KI=MK+KQ
≥

MQ
Nếu PI=MQ thì MIQP là hình chữ nhật hay
PQ PM⊥
(điều này không xảy ra)
Vậy PD>MQ (đpcm)
B
A
C
D
M
O
I
P
Q
K
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NAM
ĐỀ THI CHÍNH THỨC
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
NĂM HỌC 2012-2013
Môn thi: TOÁN
Thời gian làm bài: 150 phút, không kể thời gian giao đề
Bài 1. (4,0 điểm) Cho biểu thức:
( )(1 ) ( )( 1) ( 1)(1 )
x y xy
P
x y y x y x x y
= − −
+ − + + + −
1. Rút gọn biểu thức P.

2. Tìm các giá trị x, y nguyên thỏa mãn P = 2.
Bài 2. (4,0 điểm)
1. Cho hai số thực a, b không âm thỏa mãn
18 4 2013a b+ ≥
. Chứng minh rằng phương trình sau luôn có
nghiệm:
2
18 4 671 9 0ax bx a+ + − =
.
2. Tìm tất cả các nghiệm nguyên x, y của phương trình
3 2 3
2 3 2x x x y
+ + + =
.
Bài 3. (4,5 điểm)
1. Cho p và 2p + 1 là hai số nguyên tố lớn hơn 3. Chứng minh rằng 4p + 1 là một hợp số.
2. Giải phương trình:
2 3 2
4 3 3 4 3 2 2 1
+ + = + + −
x x x x x
Bài 4. (6,0 điểm)
Cho góc xOy có số đo bằng 60
o
. Đường tròn có tâm K nằm trong góc xOy tiếp xúc với tia Ox tại M và tiếp xúc với
tia Oy tại N. Trên tia Ox lấy điểm P thỏa mãn OP = 3OM. Tiếp tuyến của đường tròn (K) qua P cắt tia Oy tại Q khác
O. Đường thẳng PK cắt đường thẳng MN ở E. Đường thẳng QK cắt đường thẳng MN ở F.
1. Chứng minh tam giác MPE đồng dạng với tam giác KPQ.
2. Chứng minh tứ giác PQEF nội tiếp được trong đường tròn.
3. Gọi D là trung điểm của đoạn PQ. Chứng minh tam giác DEF là một tam giác đều.

Bài 5. (2,0 điểm) Cho a, b, c là ba số thực dương thỏa mãn:
3a b c+ + =
. Chứng minh rằng:
2 2 2
1 1 1
3
1 1 1
a b c
b c a
+ + +
+ + ≥
+ + +
Đề thi HSG tỉnh lớp 9 TP Hà Nội năm học 2012-2013.

SỞ GIÁO VÀ ĐÀO TẠO
HÀ TĨNH
KỲ THI CHỌN HỌC SINH GIỎI TỈNH
LỚP 9 THCS NĂM HỌC 2012-2013
Bài 1: a) Tính giá trị biểu thức:
3
( ) 3( )( 1)M x y x y xy= − + − +
, biết

3 3 3 3
3 2 2 3 2 2 , 17 12 2 17 12 2x y= + − − = + − −
b) Giải phương trình:
2 2
2 5
1 1 3
x x

x x x x
− =
− + + +
Bài 2: a) Giải hệ phương trình:
2 2
3 3 2
3 4 (1)
12 6 +9 (2)
x y x
x x y x

+ + =


+ + =


b) Tìm các số tự nhiên a, b, c phân biệt sao cho biểu thức sau nhận giá trị nguyên
( 1)( 1)( 1)ab bc ca
P
abc
− − −
=
Bài 3: Tam giác ABC có chu vi bằng 1, các cạnh a, b, c thoả mãn đẳng thức:
3
1 1 1 2
a b c
a b c
+ + =
− − −

Chứng minh tam giác ABC đều.
Bài 4: Cho tam giác ABC vuông cân tại A, gọi D là trung điểm của cạnh BC. Lấy M bất
kỳ trên đoạn thẳng AD (M không trùng với A). Gọi N, P theo thứ tự là hình chiếu
vuông góc của M xuống các cạnh AB, AC và H là hình chiếu vuông góc của
N xuống đường thẳng PD.
a) Chứng minh AH vuông góc với BH
b) Đường thẳng qua B song song với AD cắt đường trung trực của AB tại I.
Chứng minh ba điểm H, N, I thẳng hàng.
Bài 5: Các số thực dương x, y, z thoả mãn điều kiện: x + y +z = 1.