Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
72
Chơng 6- ứng dụng matlab-simulink mô phỏng các
hệ thống điều khiển tự động
6.1- Khái niệm chung
Nh đã trình bày ở các chơng trớc đây, phơng pháp mô phỏng đợc ứng dụng vào
nhiều lĩnh vực khác nhau. Ngày nay ngời ta đã phát triển nhiều phần mềm chuyên dụng dùng
cho mô hình hoá và mô phỏng. Một trong những phần mềm đợc ứng dụng rộng rãi hiện nay
là MATLAB - SIMULINK đợc dùng để mô phỏng các hệ thống động học. Phần mềm này
cung cấp cho các kỹ s, các cán bộ kỹ thuật một công cụ tính toán mạnh, một phơng tiện mô
phỏng, phân tích và tổng hợp các hệ thống động học.
MATLAB (Matrix Laboratory) là một môi trờng tính toán trên ma trận rất mạnh.
Matlab đợc tích hợp một số Toolbox, đó là th viện của các hàm hỗ trợ cho Matlab giải các
ứng dụng riêng biệt nh: hệ thống điều khiển, xử lý tín hiệu, tối u hoá, nhận dạng, điều khiển
bền vững v.v
SIMULINK (trớc đây gọi là SIMULAB) là một môi trờng mô phỏng dựa trên nền
Matlab và các Toolbox hệ thống điều khiển
(Control System) và xử lý tín hiệu (Signal
Processing). Vì vậy Simulink đợc coi là phần mở rộng của Matlab đợc dùng để mô phỏng
hệ thống động học. Simulink cho phép lập trình ở dạng sơ đồ cấu trúc cho nên rất thuận tiện
trong việc mô phỏng và khảo sát các hệ thống điều khiển tự động.
6.2- Giới thiệu về Matlab- Simulink
6.2.1- Matlab
Matlab đợc phát triển bởi công ty MathWork Inc - là một chơng trình phân tích và
làm toán trên ma trận, thiết kế hệ thống điều khiển, nhận dạng hệ thống, đồ hoạ 2D, 3D.
Matlab là một môi trờng mở, cung cấp các thuật toán và khả năng lập trình cho phép ngời
sử dụng tạo ra các ứng dụng, các chơng trình riêng của mình.
Matlab có một th viện lớn gồm hơn 500 hàm toán học từ đại số tuyến tính, các hàm ma
trận đến phân tích biến đổi Fourier và các phơng pháp số phi tuyến. Matlab có một số
Toolbox đó là những th viện hàm chuyên dụng nhằm giải các bài toán trong các lĩnh vực

chuyên môn khác nhau.
Làm việc với Matlab rất đơn giản và thuận tiện. Có hai cách làm việc: làm việc với cửa
sổ lệnh và làm việc với các M-file. Khi làm việc với cửa sổ lệnh, sau dấu nhắc (
prompt) của
Matlab >> ngời sử dụng đa vào các công thức, các hàm, các lệnh để tính toán và Matlab
trả lời ngay sau mỗi lệnh. Cách làm việc này giống nh tính toán trên trang giấy, cho phép
ngời sử dụng thử các phép tính các thuật toán rất thuận tiện.
Làm việc với M-file: Matlab cho phép lập trình, chơng trình là một dãy lệnh thực hiện
một số nhiệm vụ tính toán nhất định. Chơng trình đợc ghi thành file có phần mở rộng là .m
với tên file (
filename) tự đặt đợc gọi là M.file. Để chạy chơng trình, sau dấu nhắc >> ta
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
73
gõ vào tên file không có phần mở rộng. Lúc này Matlab coi M-file nh command file hay
script file và chơng trình đợc thực hiện theo tuần tự các lệnh đã xác định. Bình thờng khi
chạy chơng trình các lệnh không hiển thị trên màn hình.
Matlab có các loại lệnh cơ bản sau:
+ Các lệnh chung và gỡ rối
+ Các lệnh làm việc với ma trận và vectơ
+ Các lệnh làm việc với các hàm và đa thức
+ Các lệnh đồ hoạ 2D và 3D
+ Các lệnh xử lý tín hiệu và phân tích hệ thống
Ngữ pháp lập trình của Matlab rất đơn giản và gần giống các ngôn ngữ bậc cao khác nh
C, Basic và Fortran. Sau đây là một số lệnh, hàm và cấu trúc thờng dùng trong lập trình.
+ Các phép toán quan hệ:
< nhỏ hơn <= nhỏ hơn hoặc bằng = = bằng
> lớn hơn >= lớn hơn hoặc bằng

= không bằng

+ Các phép toán logic: AND, OR và NOT
+ Các lệnh điều kiện và vòng lặp: for, while và if-else
Lệnh vòng lặp for có cú pháp nh sau:
For biến = biểu thức, lệnh, lệnh, , end
Các vòng for end có thể lồng vào nhau
Lệnh vòng lặp while có cú pháp nh sau:
While biểu thức, lệnh, lệnh, , end
Lệnh rẽ nhánh có điều kiện if else end. Có ba dạng cấu trúc rẽ nhánh và có cú pháp
nh sau:
If biểu thức, lệnh, lệnh, end
If biểu thức, lệnh, lệnh, else lệnh, lệnh, end
If biểu thức 1, lệnh, lệnh, elseif biểu thức 2, lệnh, lệnh, end
+ M file: Script file và Function file
Hai dạng của M.file là Script file và Function file.
Script file chứa chơng trình gồm một số lệnh để thực hiện nhiệm vụ tính toán đã định.
Khi chạy chơng trình chỉ cần gõ tên file (filename) không có đuôi mở rộng .m.
Function file là lệnh mở rộng của Matlab, tất cả các lệnh trong các Toolbox đều có dạng
function. Function có cú pháp nh sau:
Function [biến ra 1, biến ra 2,
] = filename (biến vào 1, biến vào 2 ]
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
74
Khác nhau cơ bản giữa Script và Function là Function chỉ dùng biến riêng của mình và
không tác động tới toàn bộ chơng trình. Dòng đầu tiên của Function file phải có chữ
Function
6.2.2- Simulink
Simulink đợc coi là phần mở rộng của Matlab. Simulink đợc dùng để mô phỏng các
hệ động học các hệ tuyến tính, phi tuyến, các mô hình trong thời gian liên tục hoặc gián đoạn.
Đặc điểm nổi bật của Simulink lập trình ở dạng sơ đồ cấu trúc, sử dụng các đối tợng đồ họa

(Graphic Programming). Loại lập trình hớng đối tợng này có u điểm là tính trực quan, dễ
viết và hình dung nhất là đối với những ngời lập trình không chuyên nghiệp. Simulink cung
cấp giao diện đồ họa để xây dựng mô hình ở dạng sơ đồ khối. Bằng thao tác nhấn và kéo
chuột ngời sử dụng có thể kéo các khối chuẩn trong th viện của Simulink ra vùng làm việc
của mình để xây dựng mô hình mô phỏng.
Ngời sử dụng có thể thay đổi hoặc tạo ra khối riêng của mình và bổ sung vào th viện
nh là một khối ứng dụng mới. Simulink có các th viện sau: th viện các khối nguồn tín hiệu
(Sources), th viện các khối xuất và hiển thị dữ liệu (Sink), th viện các phần tử tuyến tính
(Linear), th viện các phần tử phi tuyến (Nonlinearr), th viện các khối gián đoạn (Discrete),
th viện các khối nối (Connections), th viện các khối phụ (Extras).
Mô hình trong Simulink đợc xây dựng theo kiểu phân cấp điều đó cho phép ngời sử
dụng có thể xây dựng mô hình theo hớng từ dới lên trên hoặc từ trên xuống dới. Dùng
chức năng tạo mặt nạ (Mask) của Simulink ngời ta có thể xây dựng các hệ con (phân hệ)
bằng cách tạo hộp thoại và biểu tợng mới cho khối.
ứng dụng quan trọng của mặt nạ là tạo ra
hộp thoại để tiếp nhận thông số của các khối trong hệ con, ngoài ra mặt nạ còn làm cho mô
hình đơn giản, rõ ràng và bảo vệ nội dung của khối khỏi sự xâm nhập của ngời lạ. Khi thực
hiện mô phỏng bằng Simulink ngời sử dụng vừa có thể quan sát hệ thống ở mức tổng quan,
vừa có thể xem xét chi tiết hoạt động của từng khối bằng cách nháy đúp chuột vào khối đó.
Các khối Scope và khối hiển thị khác (lấy trong th viện Sinks) cho phép ngời sử dụng quan
sát kết quả trong khi đang chạy mô phỏng. Hơn nữa ngời sử dụng còn có thể trực tiếp thay
đổi thông số trong khi đang chạy mô phỏng để biết đợc ảnh hởng của các thông số đó đối
với kết quả của mô phỏng.
Simulink có một đặc tính quan trọng là khi ta xây dựng mô hình dạng sơ đồ khối thì
Simulink tự động tạo ra một M.file (function) cho mô hình đó. Hàm này đợc gọi là S-
function. Cũng giống nh các hàm khác của Matlab, hàm S-function là một file mở, ngời sử
dụng có thể truy nhập vào và soạn thảo. Lệnh để mở một S-function là sfun. Điều đó có nghĩa
là có thể soạn thảo chơng trình mô phỏng mà không cần thông qua giao diện đồ thị. Mặt
khác, Simulink cho phép chuyển đổi từ S-function sang sơ đồ khối và ngợc lại. Nh vậy rất
thuận tiện cho ngời sử dụng.

Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
75
6.3- ứng dụng Matlab - Simulink để phân tích và khảo sát hệ thống điều
khiển tự động trong miền thời gian và tần số
Trong phần này sẽ trình bày một số lệnh của Matlab dùng để phân tích các hệ điều khiển
kinh điển, các lệnh này cũng có trong Control System Toolbox của Matlab.
Cho hàm truyền của một hệ điều khiển tự động G(s) = B(s)/A(s), trong đó B(s) - biểu
thức tử số (numerator) và A(s) - biểu thức mẫu số (denominator). Chúng ta quan tâm đáp ứng
của hệ thống trong miền thời gian cũng nh trong miền tần số đối với các tín hiệu vào khác
nhau nh hàm xung, hàm bớc nhảy, hàm điều hòa v.v

a). Miền thời gian
Chất lợng của các hệ thống tự động điều khiển thờng đợc đánh giá dựa trên đáp ứng
thời gian ứng với các tín hiệu vào khác nhau. Vì vậy đáp ứng thời gian có vai trò quan trọng
trong việc phân tích và tổng hợp hệ thống.
Để tìm đáp ứng của hệ G(s) khi tín hiệu vào là hàm bậc thang đơn vị 1(t) Matlab dùng
lệnh step. Cú pháp nh sau:
>> y = step(num, den, t)
Trớc tiên phải xác định trục thời gian t là một vectơ. Giá trị đáp ứng ra cũng là một
vectơ có cùng kích thớc với vectơ t. Ví dụ vẽ đờng cong đáp ứng của hàm 1(t) trong quãng
thời gian từ t = 0 đến t = 10 sec, mỗi bớc tính là 0,1 sec của hệ thống có hàm truyền đạt sau
đây:
2
10
G(s)
s2s10
=
++


Các dòng lệnh sau đây sẽ vẽ đờng cong đáp ứng nói trên:
>>num = 10; den = [1 2 10];
>>t = [0:0.1:10]; y = step (num, den, t); plot(t,y) ;
Lệnh impulse sẽ cho ta đáp ứng ra khi tín hiệu đầu vào là xung. Cú pháp nh sau :
>>y = impulse (num, den, t);
Trong trờng hợp đầu vào là hàm bất kỳ thì dùng lệnh lsim. Cú pháp nh sau :
>>y = lsim (num, den, u, t);
Trong đó u là vectơ tín hiệu đầu vào. Ví dụ đầu vào là hàm dốc ramp, cú pháp nh sau :
>> ramp = t ; y = lsim (num, den, ramp, t) ;
Nếu hàm vào là hàm rand(m,n) sẽ sinh ra ma trận m
ìn số ngẫu nhiên phân bố đều trong
khoảng (0,1), cú pháp nh sau :
>>noise = rand(m,n) ; y = lsim (num, den, rand, t) ;
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
76
Đáp ứng đầu ra khi đầu vào là hàm 1(t), khi điều kiện đầu bằng không, đợc gọi là đặc
tính quá độ h(t) của hệ thống. Từ đặc tính quá độ có thể xác định đợc các chỉ tiêu chất lợng
của hệ thống sau :
- Độ quá điều chỉnh (Percent Overshoot)
max
hh
% 100%
h



=

- Thời gian cực đại t

max
(Peak time) là quãng thời gian để đờng quá độ đạt giá trị
cực đại h
max

- Thời gian tăng t
r
(Rise time) là quãng thời gian từ khi đờng quá độ đạt 10%h


đến 90%h


- Thời gian quá độ (Settling time) là quãng thời gian từ t = 0 đến khi đờng h(t) đi
vào vùng
5%h

.
Có thể lập chơng trình để tính các chỉ tiêu chất lợng của hệ thống dới dạng một M-
files.
Ví dụ 1 dới đây sẽ minh họa đáp ứng của hệ thống với hàm truyền
=
++
2
5
G(s)
s3s20

trong thời gian từ 0 đến 10 giây, thời gian lấy mẫu là 0,1s ứng với 3 trờng hợp: (1) tín hiệu
đầu vào là bớc nhảy, (2) tín hiệu đầu vào là xung hoặc (3) tín hiệu đầu vào là ngẫu nhiên.

Chơng trình viết dới dạng Scripts
% Dap ung cua he thong voi cac tin hieu dau vao khac nhau
% Ten chuong trinh: gtmh1.m
num=5; den=[1, 3, 20];
t=[1: 0.1: 10];
disp(Bam phim 1 neu tin hieu vao la xung);
disp(Bam phim 2 neu tin hieu vao la buoc nhay);
disp(Bam phim 3 neu tin hieu vao la tin hieu ngau nhien);
a=input(Ban chon dang tin hieu nao:);
switch a
case 1
y= impulse(num,den,t);
plot(t,y,m) ;
title(Dap ung he thong voi tin hieu xung) ;
case 2
y=step(num,den,t) ;
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
77
plot(t,y) ;
title(Dap ung he thong voi tin hieu buoc nhay) ;
case 3
noise=rand(101,1);
y=lsim(num,den,noise,t) ;
plot(t,y,g) ;
title(Dap ung he thong voi tin hieu ngau nhien);
end
xlabel(Time[sec]);
ylabel(y);
Chạy chơng trình

Từ cửa sổ lệnh, chúng ta gõ tên Script file là gtmh1, sau đó đa vào giá trị chọn của
dạng tín hiệu trong chỉ dẫn trên màn hình, ví dụ chọn dạng tín hiệu là bớc nhảy, chúng ta
bấm phím 2.
>> gtmh1
Bam phim 1 neu tin hieu vao la xung
Bam phim 2 neu tin hieu vao la buoc nhay
Bam phim 3 neu tin hieu vao la tin hieu ngau nhien
Ban chon dang tin hieu nao:2
>>
Đáp ứng của hệ thống đợc
hiển thị trên Figure hình 6.1.
b). Miền tần số
Các đáp ứng tần số cho ta
một cách nhìn trực quan về chất
lợng hệ thống do nó cho ta thấy
rõ bản chất vật lý và ảnh hởng
của các phần tử lên chất lợng hệ
thống. Vì vậy các đáp ứng tần số,
hay còn gọi là đặc tính tần số, cho
ta công cụ tốt để hiệu chỉnh hệ
thống.
Có thể dùng các lệnh sau
đây để tìm đáp ứng tần số của hệ thống: bode, nyquist và nichols. Cú pháp của lệnh bode nh
sau:
Hình 6.1- Đáp ứng thời gian của hệ ĐKTĐ
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
78
>> bode (num, den)
Lệnh trên sẽ vẽ đồ thị biên độ (đơn vị là dB) và pha (đơn vị là độ). Từ đờng đặc tính tần

số ta có thể xác định đợc các chỉ tiêu chất lợng trong miền tần số nh:
- Cộng hởng đỉnh M
p
, dB, là giá trị cực đại của đồ thì biên độ;
- Tần số cộng hởng
r
, rad/s, là tần số tại đó xuất hiện cộng hởng đỉnh;
- Tần số cắt
c
, rad/s, là tần số tại đó đờng đặc tính tần số biên độ loga cắt trục
thực.
- Băng thông
B
, rad/s, là giải thông của hệ thống từ tần số bằng không đến tần số
mà ở đó biên độ giảm đi 3 dB.
Các chỉ tiêu chất lợng trong miền thời gian và trong miền tần số có quan hệ chặt chẽ
với nhau. Thông thờng độ quá điều chỉnh
% lớn thì M
P
cũng lớn tơng ứng. Giá trị cộng
hởng đỉnh tối u là nằm trong khoảng 1,1
M
P
1,5. Thời gian quá độ t
s
lớn thì M
P
nhỏ vì
vậy hệ thống tác động chậm. Băng thông


B
rộng thì các tín hiệu tần số cao đợc đa tới hệ
thống nhiều hơn nên đáp ứng của hệ sẽ nhanh hơn và ngợc lại.
Ví dụ 2 sau đây sẽ minh họa đáp
ứng tần số của hệ thống điều khiển tự
động có hàm truyền G(s) đợc mô tả
trong ví dụ 1.
Chơng trình viết trên Scrips nh
sau:
% Dap ung tan so
% Ten chuong trinh: gtmh2
num=5; den=[1,3,20];
bode(num, den)
Chúng ta nhận đợc đặc tính biên
độ (thứ nguyên là dB) và pha (độ) trên màn hình đồ họa nh hình 6.2
6.4- ứng dụng Matlab - Simulink để phân tích và khảo sát hệ thống điều
khiển tự động trong không gian trạng thái
So với phơng pháp biểu diễn hệ thống điều khiển tự động bằng hàm truyền đạt Laplace,
phơng pháp biểu diễn bằng phơng trình không gian trạng thái có một số u điểm sau: hệ
phơng trình mô tả hệ thống là hệ phơng trình bậc nhất nên tơng ứng đơn giản trong tính
toán đồng thời các hệ số là các ma trận nên dùng MATLAB để giải rất thuận tiện. Phơng
trình không gian trạng thái đợc viết trực tiếp trong miền thời gian vì vậy rất tiện cho việc giải
bằng máy tính. Các hệ nhiều đầu vào nhiều đầu ra (MIMO) và các hệ phi tuyến không dừng
thờng đợc biểu diễn bằng không gian trạng thái.
Hình 6.2- Đáp ứng tần số của hệ ĐKTĐ
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
79
Hệ thống tuyến tính dừng (LTI-linear time invariant) đợc mô tả bởi ba mô hình cơ bản
là mô hình hàm truyền (TF-Transfer Function), mô hình điểm không - điểm cực - khuyếch đại

(ZPK-Zero-Pole-Gain) và mô hình không gian trạng thái (SS - State Space).
Sau đây là các ví dụ về các dạng mô hình nói trên
- Mô hình hàm truyền (TF)

+

+
+++
=
+++
nn1
12 n1
mm1
12 m1
p s p s p
G(s)
q
s
q
s
q

Ví dụ 3:
=
++
2
2s
G(s)
s3s20


Mô hình hàm truyền đợc biểu diễn trên Matlab nh sau:
>> num = [2 0]; % Tu so: s
>> den = [1 3 20]; % Mau so: s^2+3s+20
>> H = tf(num, den) % Ham truyen
Transfer function:
2 s

s^2 + 3 s + 20
>>
- Mô hình điểm không - điểm cực - khuyếch đại (ZPK)

=

12 n
12 m
(s z )(s z ) (s z )
G(s) K
(s
p
)(s
p
) (s
p
)

với K là hệ số khuyếch đại
z
1
z
n

là các điểm không (zeros) của G(s)
p
1
p
m
là các điểm cực (poles) của G(s)
Ví dụ 4: Xác định trên Matlab hàm truyền dạng ZPK của hàm truyền G(s) nh sau:
=
+
s
G(s) 2
(s 2)(s^ 2 2s 2)

Giải:
>> k = -2;
>> z = 0;
>> p = [2 1+i 1-i];
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
80
>> G = zpk(z,p,k)
Zero/pole/gain:

+
2s
(s 2)(s ^ 2 2s 2)

>>
- Mô hình không gian trạng thái:
=

+
=+
&
x(t) A(t) Bu(t)
y
(t) Cx(t) Du(t)

Trong đó x(t) là vectơ trạng thái kích thớc n
ì1 và các thành phần của nó đợc gọi là
các biến trạng thái. Trong trờng hợp chung, nếu hệ thống có bậc n, có p tín hiệu vào và m tín
hiệu ra thì các ma trận có kích thớc nh sau:
A = n
ì n, B = n ì p, C = m ì n, D = m ì p.
A là ma trận hệ thống, B là ma trận hằng số. Ma trận C liên hệ đầu ra hệ thống với các
biến trạng thái, ma trận D liên hệ trực tiếp đầu vào u(t) với đầu ra y(t) của hệ thống. Vectơ vào
u(t) có kích thớc p
ì p và vectơ ra y(t) có kích thớc m ì p.
Để xây dựng phơng trình trạng thái ngời ta phải chuyển phơng trình vi phân bậc n
biểu diễn ĐKTĐ thành n phơng trình vi phân bậc nhất đối với vectơ trạng thái. Do chọn biến
trạng thái là không đơn trị nên có nhiều dạng phơng trình trạng thái. Thông thờng phơng
trình trạng thái đợc viết dới dạng chuẩn điều khiển đợc - CCF (Canonical controllable
form) và dạng chuẩn quan sát đợc - COF (Canonical observable form).
Ví dụ 5: Phơng trình trạng thái đơn giản của một động cơ điện có dạng nh sau:
=+
=+
&
x(t) A(t) Bu(t)
y
(t) Cx(t) Du(t)
Với

[][]

=== =



01 0 y
A ; B ; C 1 0 ; D 0 ; x
52 3 dy

Xác lập hệ phơng trình trạng thái của hệ trên Matlab.
Giải: Lập M-file nh sau:
% Mo hinh khong gian trang thai
% Ten file: gtmh3
A = [2 3;-3 -1];
B = [0; 5]; C = [1 7]; D = 0; G = ss(A,B,C,D)
Kết quả hiển thị nh sau
>> gtmh3
a =
x1 x2
x1 2 3
x2 -3 -1
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
81
b =
u1
x1 0
x2 5
c =

x1 x2
y1 1 7
d =
u1
y1 0
Để viết phơng trình trạng thái cần xác định bốn ma trận [A,B,C,D], chúng ta có thể
dùng các lệnh sau đây của MATLAB để chuyển từ hàm truyền và hàm điểm không - điểm cực
- khuyếch đại sang dạng phơng trình trạng thái và ngợc lại.
>> [a, b, c, d] = tf2ss(num, den);
>> [a, b, c, d] = zp2ss(z, p, k);
>> [num, den] = ss2tf(a, b, c, d, ui);
>> [z, p, k] = ss2zp (a, b, c, d, ui);
Biến đầu vào của tf2ss là tử số và mẫu số của hàm truyền đạt cho dới dạng vectơ hàng
(num, den). Biến đầu vào của zp2ss là số điểm không - điểm cực và hệ số khuyếch đại cho
dới dạng vectơ cột (z, p, k). Các phơng trình trạng thái nhận đợc khi dùng các lệnh tf2ss,
zp2ss đợc viết dới dạng chuẩn điều khiển đợc - CCF.
Khi biết phơng trình trạng thái có thể dùng lệnh ss2tf để chuyển sang dạng hàm truyền
đạt và lệnh ss2zp để chuyển sang dạng hàm số điểm không - điểm cực và hệ số khuyếch đại.
Trong các lệnh trên tham số ui là số đầu vào cho hệ MIMO.
Ví dụ 6: Hãy tìm phơng trình trạng thái của hệ thống có hàm truyền sau:
++
=
+++
2
32
s5s2
G(s)
s 7s 20s 15

>> num = [1 5 2]; den = [1 7 20 15];

>> [a, b, c, d
] = tf2ss(num, den)
Kết quả nhận đợc các ma trận của phơng trình trạng thái:
a =
-7 -20 -15
1 0 0
0 1 0
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
82
b =
1
0
0
c =
1 5 2
d =
0
Ví dụ 7: Hãy tìm hàm truyền của hệ thống có phơng trình trạng thái sau:


=+




&
&
&
11

22
33
x010x10
x011x0u
x123x0

y = 1 0 0x
Ta có các ma trận
A = [0 1 0 ; 0 1 1 ; -1 -2 -3] ; B = [10 ; 0 ; 0] C = [1 0 0] ; D = [0] ;
[num, den] = ss2tf(A, B, C, D)
Kết quả nhận đợc
num =
0 10 30 20
den =
1 3 2 1
Vậy hàm truyền đạt của hệ thống có dạng:
+
+
=
+
++
2
32
10s 30s 20
G(s)
s3s2s1

6.5- ứng dụng Simulink để mô hình hóa, mô phỏng, phân tích và khảo sát
các hệ thống động học
SIMULINK là phần mở rộng của MATLAB dùng để mô hình hóa các hệ động học. Giao

diện đồ họa trên màn hình của SIMULINK cho phép thể hiện hệ thống dới dạng sơ đồ cấu
trúc rất quen thuộc. Trong quá trình mô phỏng ta có thể trích tín hiệu tại vị trí bất kỳ của sơ đồ
và hiển thị tín hiệu đó trên màn hình hoặc cất giữ vào bộ nhớ, điều đó rất thuận tiện trong việc
khảo sát hệ thống.
Dới đây là một số ví dụ về ứng dụng SIMULINK trong khảo sát đặc tính của các hệ
thống thờng gặp trong lý thuyết điều khiển tự động và hệ thống điện cơ.
Ví dụ 8:
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
83
Sơ đồ khối của hệ phi tuyến gồm khâu khuyếch đại bão hòa





Xây dựng mô hình trên Simulink


Đặc tính của hệ thống hiển thị trên
Scope có dạng nh hình 6.5
Ví dụ 9: Giải phơng trình vi phân
bậc 2 Van der Pol
x + (x
2
-1)x + x = 0
Xây dựng chơng trình trên
Simulink (xem hình 6.6)
Kết quả trên Scope cho chúng ta
đặc tính của x và x (hình 6.7)

1
s

1
s

u
e
y
x
Hình 6.3- Sơ đồ khối của hệ điều khiển tự động
Hình 6.4- Thực hiện mô hình trên Simulink
H
ình 6.5- Kết quả mô phỏn
g

Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
84

ứng dụng mô phỏng trong khảo
sát các hệ thống điện cơ
Trong các hệ thống truyền động
tự động thờng có yêu cầu về điều
chỉnh dòng điện và tốc độ. Việc tổng
hợp các mạch vòng điều chỉnh dòng
điện và tốc độ đợc thực hiện nhờ việc
áp dụng các tiêu chuẩn tối u mô dun
hoặc mô đun đối xứng. Trên cơ sở cấu
trúc các bộ điều chỉnh tổng hợp đợc,

chúng ta có thể tiến hành khảo sát các
đặc tính của hệ thống trên MATLAB -
SIMULINK. Các ví dụ dới đây sẽ
trình bày hệ thống truyền động điều
chỉnh dòng điện và tốc độ động cơ
điện một chiều kích từ độc lập.
Ví dụ 10: Vẽ đặc tính dòng điện
và tốc độ của động cơ một chiều kích từ độc lập. Các thông số định mức của động cơ đợc ghi
trong lý lịch của động cơ nh sau:
Công suất định mức: P
đm
= 1,5 kW; Dòng điện định mức: I
đm
= 8,7 A;
Điện áp định mức: U
đm
= 200 V; Tốc độ định mức: n
đm
= 1440 vòng/phút.
Hình 6.6- Sơ đồ Simulink giải phơng trình VanderPol
H
ình 6.
7
- Đặc tính x và x của PT VanderPol
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
85
H
ình 6.9- Mô hình Simulink của động cơ một chiều kích từ độc lập
Phơng trình cân bằng điện áp mạch phần ứng có dạng biến đổi Laplace nh sau:

U(p) = R

I(p)(1+pT

) + K
Phơng trình cân bằng mô
men điện từ và mô men tải
K
I(p) M
c
(p) = Jp(p)
Từ các thông số định mức có
thể tính toán các thông số cơ bản
khác:
= =
dm
dm
dm dm
1000P
UI

R

= 0.5(1-
đm
)U
đm
/I
đm
=

=
=

u
U
L
PI



==
dm dm u
dm
dm
9,55(U I R )
K
n

Chơng trình mô phỏng dòng điện và tốc độ động cơ đợc viết trên Simulink nh sau:


Đặc tính dòng điện và tốc độ động cơ một chiều nh sau:









Ví dụ 11: Mạch vòng điều chỉnh dòng điện và tốc độ
1
J
p
U
-E
I

u
u
1R
1
p
T+
K


M
c

K


Hình 6.8- Sơ đồ cấu trúc của động cơ điện một chiều
kích từ độc lập
H
ình 6.10- Kết quả mô phỏng động cơ một chiều kích từ độc lập
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
86

Sơ đồ cấu trúc tổng quát của hệ thống điều chỉnh dòng điện và tốc độ của động cơ điện
một chiều nh sau:








Các hàm truyền của các phần tử trong mạch đợc tính toán và tổng hợp nh sau:
Hàm truyền bộ biến đổi
==
+
+
bd
bd
bd
K
22
W
1 T s 0.005s 1

Hàm truyền bộ đo dòng điện
==
+
+
I
I
I

K
0.79
W
1Ts 0.001s1

Hàm truyền bộ điều chỉnh dòng
+
=+=
iI
RI pI
K
10.06s
WK
s 0.12s

Hàm truyền máy phát tốc
FT
0.9689
W
0.001s 1
=
+

Hàm truyền bộ điều chỉnh tốc độ
I
Rp
K
10.056s
WK
s0.019s



+
=+=
Mô men tải M
c
trong trờng hợp này đợc chọn bằng 0.
Chơng trình mô phỏng thực hiện trên Simulink nh sau:

bd
bd
K
1T
p
+
I
I
K
1T
p
+
1
J
p

-E
I




1R
1
p
T+
K


M
c

K


H
ình 6.11- Sơ đồ cấu trúc hệ điều khiển ĐCMC với 2 mạch vòng phản hồi


+
K
1T
p
R
I
R


U

đ


Gi¸o tr×nh M« h×nh ho¸
Bé m«n Tù ®éng ho¸ Khoa §iÖn
87
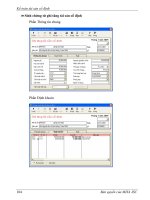
trong dã th«ng sè cña c¸c khèi nh− sau:



Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
88
Kết quả mô phỏng đợc hiển thị trên các scope nh sau:
- Đặc tính tốc độ:
- Đặc tính dòng điện:

Trên đây là ví dụ đơn giản về mô phỏng hệ truyền động động cơ một chiều. Bạn đọc có
thể phát triển mô phỏng các hệ thống điều khiển tự động khác phức tạp hơn.
Giáo trình Mô hình hoá
Bộ môn Tự động hoá Khoa Điện
89
Ti liệu tham khảo
1. Averill M. Law, W. David Kelton (1991). Simulation Modeling and Analysis.
McGraw-Hill, Inc.
2. Geoffrey Gordon. System Simulation. (1989). Prentice-Hall of India Private Limited.
3. Setwart V. Hoover, Ronald F. Perry. (1989) Simulation. A Problem-Solving
Approach. Addison-Wesley Publishing Company.
4. Barry L. Nelton. (1995). Stochastic Modeling McGraw-Hill, Inc.
5. Pastijn Hugo. (1997). Introduction Simulation. AIT. Bangkok.
6. Voratas Kachitrychianukul. (1998). Discret Event Simulation of Production System.
AIT. Bangkok.
7. Sheldon M. Ross. A Course in Simulation. Macnillan Publishing Company. New

York.
8. Worksims94. (1994). Simulation in Manufacturing System. AIT Bangkok.
9. James H. Taylor. Modeling and Simulation of Nonlinear Dynamic Systems. (2002).
JUV RSCCE02. Danang Vietnam.
10. Ouassima Alchrif. Mohsen Ghribi. (1994). Techniques de Simulation. Ecole de
technologie superieure. Quybec. Canada.
6. Landau I. Done. (1988). Identification et Commande des Systems. Hermes.
12. Bahram Shahian, Michael Hassul. (1993). Control System Design Using MATLAB.
Pentice-Hall.
13. Benjamin C. Kuo. (1995). Automatic Control Systems. Prentice-Hall.
14. Katsuhiko Ogata. (2001). Modern Control Engineering. Fourth Edition. Prentice-
Hall.
15. Nguyễn Công Hiền (2005). Mô hình hoá hệ thống và mô phỏng. ĐHBK HN.
16. Thân Ngọc Hoàn (2002). Mô phỏng hệ thống điện tử công suất và truyền động điện.
Nxb Xây dựng. Hà nội.
17. Tống Đình Quỳ (2002). Giáo trình xác suất thống kê. NXB Giáo dục.
18. Nguyễn Công Định. (2002). Phân tích và tổng hợp các hệ thống điều khiển máy tính.
NXB Khoa học và Kỹ thuật. Hà nội.