Bài giảng đồ họa : Các thuật toán vẽ đường part 1 potx
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (85.77 KB, 5 trang )
ĐỒ HỌA MÁY TÍNH
Dương Anh Đức, Lê Đình Duy Các thuật toán vẽ đường 1/22
C
C
a
a
ù
ù
c
c
t
t
h
h
u
u
a
a
ä
ä
t
t
t
t
o
o
a
a
ù
ù
n
n
v
v
e
e
õ
õ
đ
đ
ư
ư
ơ
ơ
ø
ø
n
n
g
g
D
D
a
a
ã
ã
n
n
n
n
h
h
a
a
ä
ä
p
p
• Giả sử tọa độ các điểm nguyên sau khi xấp xỉ đối
tượng thực lần lượt là
(
)
,
0
,
,
=
i
y
x
ii
. Đây là các điểm
nguyên sẽ được hiển thò trên màn hình.
• Bài toán đặt ra là nếu biết được
(
)
ii
y
x
,
là tọa độ
nguyên xác đònh ở bước thứ i, điểm nguyên tiếp theo
(
)
11
,
++ ii
y
x
sẽ được xác đònh như thế nào.
• Đối tượng hiển thò trên lưới nguyên được liền nét,
các điểm mà
(
)
11
,
++ ii
y
x
có thể chọn chỉ là một trong
tám điểm được đánh số từ 1 đến 8 trong hình sau
(điểm đen chính là
(
)
ii
y
x
,
).Hay nói cách khác :
(
)
(
)
1
,
1
,
11
±
±
=
++ iiii
y
x
y
x
.
• Dáng điệu của đường sẽ cho ta gợi ý khi chọn một
trong tám điểm trên. Cách chọn các điểm như thế
nào sẽ tùy thuộc vào từng thuật toán trên cơ sở xem
xét tới vấn đề tối ưu tốc độ.
1
23
876
5
4
ĐỒ HỌA MÁY TÍNH
Dương Anh Đức, Lê Đình Duy Các thuật toán vẽ đường 2/22
T
T
h
h
u
u
a
a
ä
ä
t
t
t
t
o
o
a
a
ù
ù
n
n
v
v
e
e
õ
õ
đ
đ
ư
ư
ơ
ơ
ø
ø
n
n
g
g
t
t
h
h
a
a
ú
ú
n
n
g
g
• Xét đoạn thẳng có hệ số góc
1
0
<
<
m
và
0
>
Dx
.
• Với các đoạn thẳng dạng này, nếu
(
)
ii
y
x
,
là điểm
đã xác đònh được ở bước thứ i (điểm màu đen) thì
điểm cần chọn
(
)
11
,
++ ii
y
x
ở bước thứ (i+1) sẽ là một
trong hai trường hợp như hình vẽ sau :
{ }
+∈
+=
+
+
1,
1
1
1
iii
ii
yyy
xx
• Vấn đề còn lại, là cách chọn một trong hai điểm trên
như thế nào để có thể tối ưu về mặt tốc độ.
(x
i
+1, y
i
+1)
1
2
(x
i
+1, y
i
)
x
i
y
i
ĐỒ HỌA MÁY TÍNH
Dương Anh Đức, Lê Đình Duy Các thuật toán vẽ đường 3/22
T
T
h
h
u
u
a
a
ä
ä
t
t
t
t
o
o
a
a
ù
ù
n
n
D
D
D
D
A
A
(
(
D
D
i
i
g
g
i
i
t
t
a
a
l
l
D
D
i
i
f
f
f
f
e
e
r
r
e
e
n
n
t
t
i
i
a
a
l
l
A
A
n
n
a
a
l
l
y
y
z
z
e
e
r
r
)
)
• Việc quyết đònh chọn
1+i
y
là
i
y
hay
1
+
i
y
, dựa vào
phương trình của đoạn thẳng
b
mx
y
+
=
. Nghóa là,
ta sẽ tính tọa độ của điểm
(
)
y
x
i
,
1
+
thuộc về đoạn
thẳng thực. Tiếp đó,
1+i
y
sẽ là giá trò sau khi làm
tròn giá trò tung độ y.
• Như vậy :
(
)
( )
yRoundy
b
x
m
y
i
i
=
++=
+1
1
• Nếu tính trực tiếp giá trò thực y ở mỗi bước từ
phương trình
b
mx
y
+
=
thì phải cần một phép toán
nhân và một phép toán cộng số thực. Để cải thiện
tốc độ, người ta tính giá trò thực của y ở mỗi bước
theo cách sau để khử phép tính nhân trên số thực :
• Nhận xét rằng :
(
)
b
x
m
b
mx
y
iisau
++=+=
+
1
1
b
mx
y
itrước
+
=
m
y
y
trướcsau
+
=
⇒
(x
i
, y
i
)
(x
i
+1, y)
(x
i
+1, Round(y))
ĐỒ HỌA MÁY TÍNH
Dương Anh Đức, Lê Đình Duy Các thuật toán vẽ đường 4/22
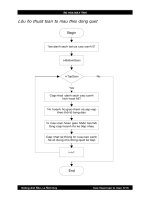
Lưu đồ thuật toán DDA
Begin
m=Dy/Dx;
x=x1;
y=y1;
putpixel(x, Round(y), c);
x<x2
Yes
No
x=x+1;
y=y+m;
putpixel(x, Round(y),c);
End
ĐỒ HỌA MÁY TÍNH
Dương Anh Đức, Lê Đình Duy Các thuật toán vẽ đường 5/22
• Ví dụ : Cho A(12, 20) và B(22, 27), ta có m= 0.7
i
i
x
x
i
i
y
y
i
i
y
y
0
0
1
1
2
2
2
2
0
0
2
2
0
0
1
1
1
1
3
3
2
2
1
1
2
2
0
0
.
.
7
7
2
2
1
1
4
4
2
2
1
1
2
2
1
1
.
.
4
4
3
3
1
1
5
5
2
2
2
2
2
2
2
2
.
.
1
1
4
4
1
1
6
6
5
5
1
1
7
7
6
6
1
1
8
8
7
7
1
1
9
9
8
8
2
2
0
0
9
9
2
2
1
1
1
1
0
0
2
2
2
2
2
2
7
7
• Cài đặt minh họa thuật toán DDA
#define Round(a) int(a+0.5)
int Color = GREEN;
void LineDDA (int x1, int y1, int x2, int y2)
{
int x = x1;
float y = y1;
float m = float(y2-y1)/(x2-x1);
putpixel(x, Round(y), Color);
for(int i=x1; i<x2; i++)
{
x++;
y +=m;
putpixel(x, Round(y), Color);
}
} // LineDDA