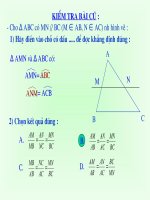KHAI NIEM TAM GIAC DONG DANG
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.2 MB, 25 trang )
SV : Phan Th Cng
Thế nào là hai tam giác đồng dạng với nhau?
Đ4
Đ4
Hãy nêu nhận xét
của em về các cặp
hình bên ?
SV : Phan Thế Cường
Trong thùc tÕ , ta th êng gÆp nh÷ng h×nh cã h×nh d¹ng
gièng nhau nh ng kÝch th íc cã thÓ kh¸c nhau. VÝ dô nh
c¸c cÆp h×nh sau:
Nh÷ng cÆp h×nh nh trªn gäi lµ nh÷ng cÆp h×nh ®ång d¹ng.
H×nh 1
H×nh 2
H×nh 3
SV : Phan Thế Cường
H×nh ®ång d¹ng lµ nh÷ng h×nh cã h×nh
d¹ng gièng nhau nh ng cã thÓ kh¸c nhau
vÒ kÝch th íc.
SV : Phan Th Cng
Nhìn vào hình vẽ hãy viết các cặp góc bằng
nhau.
Tính các tỉ số
?1
A
B
C
A
CB
4
5
6
2
3
2,5
a> Định nghĩa
Cho hai tam giác ABC và ABC
rồi so sánh các tỉ số đó.
CA
AC
BC
CB
AB
BA
;;
SV : Phan Th Cng
A
B
C
'.
;'
;'
CCBBAA ===
2
1
5
5,2''
2
1
6
3''
2
1
4
2''
==
==
==
CA
AC
BC
CB
AB
BA
Nhận thấy các tỉ số đó bằng nhau và đều bằng
.
2
1
ABC và ABC có :
A
B
C
4
5
6
2
2,5
3
Trả lời
SV : Phan Th Cng
.
;
;
;
CA
AC
BC
CB
AB
BA
CCBBAA
=
=
=
=
=
Hai tam giác đ ợc gọi là đồng dạng với nhau nếu:
. Các cặp góc t ơng ứng bằng nhau.
. Các cặp cạnh t ơng ứng tỉ lệ.
Tam giác ABC gọi là đồng dạng với tam giác ABC nếu:
SV : Phan Th Cng
Ta kí hiệu tam giác đồng dạng nh sau:
ABC ABC
Khi viết ABC ABC ta viết theo thứ tự cặp
đỉnh t ơng ứng.
Trong ta có ABC ABC với tỉ số đồng dạng là k = .
k
CA
AC
BC
CB
AB
BA
=
=
=
?
1
2
1
Tỉ số các cạnh t ơng ứng :
k gọi là tỉ số đồng dạng.
=> AB=k.AB ; BC = k.BC ; AC= k.AC
SV : Phan Th Cng
Em hãy chỉ ra các đỉnh t ơng ứng, các góc t ơng
ứng , các cạnh t ơng ứng khi ABC ABC .
A
C
A
B
C
B
SV : Phan Thế Cường
§Ønh A’ t ¬ng øng víi ®Ønh A
§Ønh B’ t ¬ng øng víi ®Ønh B
§Ønh C’ t ¬ng øng víi ®Ønh C
Gãc A’ t ¬ng øng víi gãc A
Gãc B’ t ¬ng øng víi gãc B.
Gãc C’ t ¬ng øng víi gãc C
C¹nh A’B’ t ¬ng øng víi c¹nh AB
C¹nh B’C’ t ¬ng øng víi c¹nh BC
C¹nh A’C’ t ¬ng øng víi c¹nh AC
A
C
A’
B’
B
C’
Tr¶ lêi
SV : Phan Th Cng
1> Nếu tam giác ABC = ABC thì
ABC có đồng dạng với ABC không?
Tỉ số đồng dạng là bao nhiêu?
CCBBAA
=
=
=
;
;
'';'';'' CBBCCAACBAAB ===
1=
=
=
=>
CB
BC
CA
AC
BA
AB
Vậy hai tam giác bằng nhau thì đồng dạng với nhau.
B
C
A
A
B C
Chứng Minh:
Từ ABC = ABC ta có:
Theo định nghĩa hai tam giác đồng dạng
thì ABC ABC. Tỷ số đồng dạng K=1
SV : Phan Thế Cường
TÝnh chÊt 1: Mçi tam gi¸c ®ång d¹ng víi chÝnh nã.
SV : Phan Thế Cường
VÝ dô: Cã hai b¹n An vµ B×nh lµm bµi nh sau:
An: ABC A’B’C’ theo tû sè
B×nh: A’B’C’ ABC theo ti sè K=2
Ai tr¶ lêi ®óng ? T¹i sao?
B’
C’
A’
8
10
12
2
1
=k
A
B
C
4
6
5
SV : Phan Thế Cường
======
′
=
′
=
′
=
;
2
1
10
5
''
;
2
1
12
6
''
;
2
1
8
4
''
ˆˆ
;
ˆˆ
;
ˆˆ
CA
AC
CB
BC
BA
AB
CCBBAA
======
===
;2
5
10''
;2
6
12''
;2
4
8''
ˆ
'
ˆ
;
ˆ
'
ˆ
;
ˆ
'
ˆ
CA
AC
BC
CB
AB
BA
CCBBAA
Tõ ®ã ta cã tÝnh chÊt 2: nÕu A’B’C’ ∽ ABC th× ABC
∽A’B’C’
VËy c¶ An vµ B×nh ®Òu tr¶ lêi ®óng.
2
1
=k
Tr¶ lêi
XÐt hai ABC vµ A’B’C’ cã:
Suy ra ABC A’B’C’ theo tØ sè lµ:
XÐt A’B’C’ vµ ABC cã:
Suy ra ABC A’B’C’ theo tØ sè k =2
SV : Phan Thế Cường
TÝnh chÊt 3 :
NÕu A’B’C’ A’’B’’C’’ vµ
A’’B’’C’’ ABC
th× A’B’C’ ABC
Em h·y chøng minh tÝnh chÊt
trªn.
SV : Phan Thế Cường
'
ˆˆ
''
ˆ
;'
ˆˆ
''
ˆ
;'
ˆˆ
''
ˆ
CCCBBBAAA ======
0
''''''''''''
2
≠=== k
CA
AC
BC
CB
AB
BA
21
''''"
''"
''
;21
''""
""
''
;21
''"''
"''
''
kk
CA
AC
CA
AC
AC
AC
kk
BC
CB
BC
CB
CB
CB
kk
AB
BA
AB
BA
BA
BA
×==××==××==×
"
ˆ
'
ˆ
;"
ˆ
'
ˆ
;"
ˆ
'
ˆ
CCBBAA ===
0
""
''
""
''
''"
''
1
≠=== k
AC
AC
CB
CB
BA
BA
(**)
(2)
(4)
CCBBAA
ˆ
''
ˆ
;
ˆ
''
ˆ
;
ˆ
''
ˆ
===
(*)
(1)
(3)
Chøng minh
Theo bµi ra ta cã :
A’B’C’ A’’B’’C’’
=>
A’’B’’C’’ ABC
=>
Tõ (1) vµ (2) ta cã :
;
CA
AC
BC
CB
AB
BA
′′
=
′′
=
′′
=>
Tõ (*) vµ (**) => A’B’C’ ABC (§PCM)
SV : Phan Th Cng
Trả lời
Xét AMN và ABC có:
chung.
Đồng vị
Đồng vị
Mặt khác theo hệ quả của định lí Talet hai AMN và ABC có 3
cặp cạnh t ơng ứng tỉ lệ:
Vậy AMN ABC
Cho tam giác ABC . Kẻ đ ờng thẳng a song song với cạnh BC
và cắt hai cạnh AB , AC theo thứ tự tại M và N . Hai tam
giác AMN và ABC có các góc và các cạnh t ơng ứng nh thế
nào?
?3
A
11
11
CN
BM
=
=
BC
MN
AC
AN
AB
AM
==
A
B C
M
N
1
1
2
2
a
SV : Phan Thế Cường
NÕu mét ® êng th¼ng c¾t hai c¹nh cña mét tam gi¸c vµ
song song víi c¹nh cßn l¹i th× nã t¹o thµnh mét tam
gi¸c míi ®ång d¹ng víi tam gi¸c ®· cho.
A
B C
M
N
a
SV : Phan Th Cng
Chứng minh.
GT
KL
ABC
MN // BC (MAB ;N AC )
AMN ABC
A
B C
M
N
a
Xét tam giác ABC và MN // BC (hình vẽ).
Hai tam giác AMN và ABC có:
AMN = ABC ; ANM = ACB (các cặp góc đồng vị)
BAC là góc chung.
Mặt khác theo hệ quả của định lí Talet, hai tam giác AMN và
ABC có ba cặp cạnh t ơng ứng tỉ lệ:
BC
MN
AC
AN
AB
AM
==
Vậy AMN ABC
SV : Phan Thế Cường
§Þnh lÝ còng ®óng cho tr êng hîp ® êng th¼ng a c¾t phÇn
kÐo dµi hai c¹nh cña tam gi¸c vµ song song víi c¹nh cßn
l¹i.
M N
a
A
B
C
M N
B
C
A
a
SV : Phan Thế Cường
ABC = A’B’C’ ABC A’B’C’
ABC = A’B’C’ → A’B’C’ = ABC
ABC A’B’C’ → A’B’C’ ABC
ABC = A’B’C’
A’B’C’ = A”B”C”
→ ABC = A’’ B’’C’’
ABC A’B’C’
A’B’C’ A”B”C”
→ ABC A’’ B’’C’’
'
ˆˆ
;'
ˆˆ
;'
ˆˆ
CCBBAA ===
'
ˆˆ
;'
ˆˆ
;'
ˆˆ
CCBBAA ===
1
''''''
===
CA
AC
CB
BC
BA
AB
0
''''''
≠=== k
CA
AC
CB
BC
BA
AB
SV : Phan Th Cng
Ví dụ . Cho tam giác ABC . hãy vẽ các tam giác đồng dạng với
tam giác ABC theo tỉ số k = 1/ 2
A
B
C
A
B C
B C
A A
C
B
A B
C
A
B C
A C
B
A
B C
A A
B C
B
C
Trả lời
SV : Phan Th Cng
Trong các mệnh đề sau mệnh đề nào đúng,mệnh đề nào sai:
a:Hai tam giác bằng nhau thì đồng dạng với nhau
b:Hai tam giác đồng dạng với nhau thì bằng nhau
c: Các tam giác đều thì đồng dạng với nhau
d:Các tam giác cân có một cặp góc bằng nhau
thì đồng dạng với nhau
e: Tam giác vuông ABC đồng dạng với tam giác
vuông ABC theo tỉ số k thì tỉ số diện tích của chúng là k.
f: Tam giác ABC đồng dạng với tam giác ABC theo
tỉ số k thì tỷ số chu vi của hai tam này bằng k
Phần kiểm tra trắc nghiệm
SV : Phan Th Cng
M
N
P
H K
A
B
C
A
B
C
6
10
5
4
3
8
Điền câu trả lời vào phiếu học tập.
Em hãy cho biết đáp án nào đúng ?
KM = KP
MH = HN
Quan hệ Tỉ số Đáp án
1
MHK MNP
ABC ABC
K=1/2
K= -2
2
MNP MHK
ABC ABC
K=2
K=1/2
3
MHK NMP
K= ẵ
SV : Phan Th Cng
Qua bài học hôm
nay em cần phải
ghi nhớ những
kiến thức gì?
Cần ghi nhớ :
1.Định nghĩa tam giác đồng dạng.
2.Cách xác định tỉ số đồng dạng.
3.Các tính chất.
4.Định lí về tam giác đồng dạng.
SV : Phan Thế Cường
VÒ nhµ
ph¶i lµm
nh÷ng bµi
tËp nµo?
Bµi tËp vÒ nhµ
1> Bµi tËp 23;24;25 SGK
trang 71,72
2> Bµi 25;26 trang71
s¸ch bµi tËp.