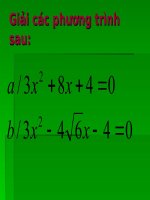luyen tap cong thuc nghiem thu gon
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (1.45 MB, 8 trang )
NhiÖt liÖt chµo mõng c¸c thÇy, c« gi¸o vÒ
dù giê líp 9A
To¸n 9
GIÁO VIÊN: PHẠM NGỌC HIẾU
TRƯỜNG THCS AN BỒI
Kiểm tra bài cũ
Câu 1: Viết công thức nghiệm thu gọn của phương trình bậc hai một ẩn?
Câu 2: Điền vào chỗ (…) để được các khẳng định đúng?
Phương trình:
a x
2
+ bx + c = 0 ( a ≠ 0 )
Và b = 2 b
/
, ∆
/
= b
/ 2
– ac.
a , Phương trình vô nghiệm ….
b , Phương trình có nghiệm kép ….
c , Phương trình có hai nghiệm phân biệt ….
d , Phương trình có nghiệm ….
e , Nếu ac < 0 thì …
Câu 3: Nêu các bước giải phương trình bậc hai một ẩn bằng công thức nghiệm thu gọn?
∆
/
< 0
∆
/
= 0
∆
/
> 0
0
′
∆ ≥
Phương trình có hai nghiệm phân biệt.
Tiết 56: LUYỆN TẬP: CÔNG THỨC NGHIỆM THU GỌN
I. Lý thuyết
II. Bài tập
Dạng 1: Giải phương trình:
Bài 1: Giải các phương trình sau:
2
a, x 2 3 5 0
2
, 3 6 3 (2 3 4)
2
, 4 6 24 0
x
b x x
c x x
− + =
+ = − −
− + =
Giải
2
, 2 3 5 0
( 1; 3; 5)
2
3 5 2 0
a x x
a b c
b ac
− + =
′
= = − =
′ ′
∆ = − = − = − <
Vậy phương trình vô nghiệm.
2
, 3 6 3 (2 3 4)b x x
+ = − −
2
(2 3 4) 6 3 3 0x x⇔ + − − + =
2
2( 3 2) 6 3 3 0x x⇔ + − − + =
( 1; 3 2; 6 3 3)a b c
′
= = − = − +
2
2
3 4 3 4 6 3 3
4 2 3 ( 3 1) 0
b ac
>
′ ′
∆ = − = − + + −
= + = +
Phương trình có 2 nghiệm phân biệt:
1
2
3 2 3 1
3
1
3 2 3 1
1 2 3
1
b
x
a
b
x
a
′ ′
− + ∆ − + + +
= = =
′ ′
− + ∆ − + − −
= = = −
2
, 4 6 24 0c x x
− + =
( 1; 2 6; 24)a b c
′
= = − =
2 2
( 2 6) 24 24 24 0b ac
′ ′
∆ = − = − − = − =
Phương trình có nghiệm kép:
1 2
2 6
b
x x
a
′
−
= = =
Tiết 56: LUYỆN TẬP: CÔNG THỨC NGHIỆM THU GỌN
I. Lý thuyết
II. Bài tập
Dạng 1: Giải phương trình:
Dạng 2: Tìm giá trị của tham số để phương
trình bậc hai có nghiệm, vô nghiệm.
Bài 2: Cho phương trình:
x
2
– 2(m – 1)x +m
2
= 0 ( với m là tham số)
1, Tính ∆
/
?
Giải:
1. Tính ∆
/
x
2
– 2(m – 1)x + m
2
= 0
2
( 1; 1 ; )a b m c m
′
= = − =
2 2 2
2 1 1 2b ac m m m m
′ ′
∆ = − = − + − = −
2, Tìm giá trị của m để :
a. Phương trình có nghiệm ?
2.Tìm m để :
a. Phương trình có nghiệm khi và chỉ khi
0 1 2 0 0,5m m
′
∆ ≥ ⇔ − ≥ ⇔ ≤
b. Phương trình có 2 nghiệm phân biệt ?
b.Phương trình có 2 nghiệm phân biệt khi và
chỉ khi ∆
/
> 0 1 – 2m > 0
m < 0,5
Vậy m < 0,5 thì phương trình có hai nghiệm
phân biệt .
c. Phương trình vô nghiệm ?
c. Phương trình vô nghiệm khi và chỉ khi
∆
/
< 0 1 – 2m < 0 m > 0,5
Vậy m > 0,5 thì phương trình vô nghiệm.
d.Phương trình có nghiệm kép và tìm
nghiệm kép đó ?
d. Phương trình có nghiệm kép khi và chỉ khi
∆
/
= 0 1 – 2m = 0
m = 0,5
Vậy m = 0,5 thì phương trình có nghiệm kép.
Với m = 0,5 thì phương trình có nghiệm kép
1 2
1 0,5 1
0,5
1 1
b m
x x
a
′
− − −
= = = = = −
Vậy với m = 0,5 thì phương trình có nghiệm
kép :
1 2
0,5x x= = −
Tiết 56: LUYỆN TẬP: CÔNG THỨC NGHIỆM THU GỌN
I. Lý thuyết
II. Bài tập
Dạng 1: Giải phương trình:
Dạng 2: Tìm giá trị của tham số để phương
trình bậc hai có nghiệm, vô nghiệm.
Bài 2: Cho phương trình:
x
2
– 2(m – 1)x +m
2
= 0 ( với m là tham số)
1, Tính ∆
/
?
Giải:
1. Tính ∆
/
x
2
– 2(m – 1)x +m
2
= 0
2
( 1; 1 ; )a b m c m
′
= = − =
2 2 2
2 1 1 2b ac m m m m
′ ′
∆ = − = − + − = −
2, Tìm giá trị của m để :
a. Phương trình có nghiệm ?
2.Tìm m để :
a. Phương trình có nghiệm khi và chỉ khi
0 1 2 0 0,5m m
′
∆ ≥ ⇔ − ≥ ⇔ ≤
b. Phương trình có 2 nghiệm phân biệt ?
b.Phương trình có 2 nghiệm phân biệt khi và
chỉ khi ∆
/
> 0 m < 0,5
Vậy m < 0,5 thì phương trình có hai nghiệm
phân biệt .
c. Phương trình vô nghiệm ?
c. Phương trình vô nghiệm khi và chỉ khi
∆
/
< 0 m > 0,5
Vậy m > 0,5 thì phương trình vô nghiệm.
d.Phương trình có nghiệm kép và tìm
nghiệm kép đó ?
d. Phương trình có nghiệm kép khi và chỉ khi
∆
/
= 0 m = 0,5
Vậy m = 0,5 thì phương trình có nghiệm kép.
Với m = 0,5 thì phương trình có nghiệm kép
1 2
1 0,5 1
0,5
1 1
b m
x x
a
′
− − −
= = = = = −
Vậy với m = 0,5 thì phương trình có nghiệm
kép :
1 2
0,5x x= = −
Cách 2:
0 m 0,5
′
∆ ≥ ⇔ ≤
Vì
Nên
Tiết 56: LUYỆN TẬP: CÔNG THỨC NGHIỆM THU GỌN
I. Lý thuyết
II. Bài tập
Dạng 1: Giải phương trình:
Dạng 2: Tìm giá trị của tham số để phương
trình bậc hai có nghiệm, vô nghiệm.
Dạng 3 : Chứng minh phương trình có
nghiệm hoặc vô nghiệm.
Bài 3 :
a.Không giải phương trình hãy giải thích tại
sao phương trình :
2008x
2
– 2009x -2010 = 0 luôn có hai nghiệm
phân biệt ?
Bài 3 :
a. ta có : a = 2008 > 0
c = - 2010 < 0
nên ac < 0 do đó phương trình có hai nghiệm
phân biệt.
b. Chứng minh rằng phương trình sau luôn
có hai nghiệm phân biệt với mọi giá trị của
m ?
x
2
– 2 (m + 3 )x + 2m + 4 = 0
c.Chứng minh rằng phương trình sau luôn
vô nghiệm với mọi giá trị của m ?
x
2
-2(m-2)x+2m
2
- 2m + 9 = 0
b.Ta có :
∆
/
= m
2
+ 6 m + 9 - 2m - 4
= (m
2
+ 4 m +4) + 1
= (m + 2)
2
+1 > 0với mọi giá trị của m vì :
2
( 2) 0m m+ ≥ ∀
Vậy phương trình luôn có hai nghiệm phân
biệt với mọi giá trị của m.
c.Ta có:
∆/ =m
2
- 4m + 4 - 2m
2
+2m - 9
= - m
2
- 2m – 5
=-( m
2
+ 2 m + 1) – 4
= - (m + 1)
2
- 4
vì :
2 2
( 1) 0 ( 1) 4 0m m m m− + ≤ ∀ ⇒ − + − < ∀
Hay ∆
/
< 0 với mọi giá trị của m
Vậy phương trình luôn vô nghiệm với mọi giá
trị của m.
Củng cố :
? Nhắc lại các dạng bài tập đã làm và cách làm các dạng bài tập đó ?
Hướng dẫn học ở nhà :
Làm các bài tập còn lại trong sách giáo khoa và làm bài 32, 33 , 34 sbt
Xin chân thành cảm ơn các thầy cô giáo và các em
học sinh !