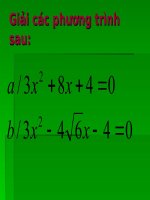I. Kiểm tra bài cũ
Xác định a, b, c rồi dùng công thức nghiệm thu
gọn giải phơng trình
0165
2
=+
xx
Đáp án: a = 5, b=-3, c = 1
2 ,41.5)3(
,2'
===
Phơng trình có 2 nghiệm phân biệt là:
5
1
5
23
;1
5
23
21
=

==
+
=
xx

II. LuyÖn tËp:
1. D¹ng 1: Gi¶i ph¬ng tr×nh.
Bµi 20 SGK/49

2
25 16 0x
− =
2
2 3 0x
+ =
a)
b)

§¸p ¸n:
2
2
) 25 16 0
16

25
16 4

25 5
a x
x
x
− =
⇔ =
⇔ =± =±
VËy ph¬ng tr×nh cã nghiÖm lµ:
4
5
x
=±


§¸p ¸n:
2
2 2
) 2 3 0
2 0 x 2 3 0 x
b x
x x
+ =
≥ ∀ ⇒ + ∀
⇒
f
V×
Ph¬ng tr×nh v« nghiÖm
Víi ph¬ng tr×nh . Em cã c¸ch gi¶i nµo kh¸c?
2
25 16 0x
− =

C¸ch 2:
2
) 25 16 0a x
− =






−=

=
⇔



=+
=−
⇔
=+−⇔
5
4
5
4
045
045
0)45)(45(
x
x
x
x
xx
VËy ph¬ng tr×nh cã nghiÖm lµ:
4
5
x
=±

VËy ph¬ng tr×nh cã nghiÖm lµ:
4
5

x
=±
C¸ch 3:
2
) 25 16 0a x
− =
20'0400)16.(250'
2
=∆⇒>=−−=∆
a = 25; b’ = 0; c = -16
5
4
25
200
5
4
25
200
2
1
−=
−
=
=
+
=
x
x

Mét HS gi¶i ph¬ng tr×nh nh sau:

5
4
25
16
25
16
1625
01625
2
2
2
==⇔
=⇔
=⇔
=−
x
x
x
x
VËy ph¬ng tr×nh cã nghiÖm lµ:
5
4
=
x
2
25 16 0x
− =
Theo em b¹n HS ®ã gi¶i ®óng hay sai? V× sao?

VËy ph¬ng tr×nh cã nghiÖm

lµ:
4
5
x
=±
C¸ch 3:
2
) 25 16 0a x
− =
2
' 0 25.( 16)
400 0 ' 20
∆ = − −
= > ⇒ ∆ =
a = 25; b’ = 0; c = -16
5
4
25
200
5
4
25
200
2
1
−=
−
=
=
+

=
x
x
C¸ch 1:
2
2
) 25 16 0
16

25
16 4

25 5
a x
x
x
− =
⇔ =
⇔ = ± =±
VËy ph¬ng tr×nh cã nghiÖm
lµ:
4
5
x
=±
So s¸nh c¸ch 1 víi c¸ch 3. Em cã nhËn xÐt g×?

Bài 21( SGK/ 49)
Giải vài phơng trình của An Khô- va- ri- zmi


19
12
7
12
1
)
28812)
2
2
=+
+=
xxb
xxa
* Với phơng trình bậc hai khuyết, nhìn chung không nên
giải bằng công thức nghiệm mà nên dùng bằng cách giải
riêng.
An Khô- va- ri- zmi là nhà toán học nổi tiếng ngời Trung á. Ông đ
ợc biết đến nh là cha đẻ của môn đại số. (Để biết rõ hơn về ông các
em về đọc mục có thể em cha biết Toán 7, tập 2, tr.26)


§¸p ¸n
2
2
,
,
,
) 12 288
12 288 0
1; 6; 288

36 288 324 0
18
a x x
x x
a b c
= +
⇔ − − =
= =− = −
∆ = + =
⇒ ∆ =
f
Ph¬ng tr×nh cã 2 nghiÖm ph©n biÖt:
1
2
6 18 24
6 18 12
x
x
= + =
= − = −

2
1 7
) 19
12 12
b x x
+ =
Nêu cách giải phơng trình phần
Hớng dẫn:
2

2
2
1 7
) 19
12 12
7 19.12
7 228 0
b x x
x x
x x
+ =
+ =
+ =
acbacb
==
22
'';4
Trở lại công thức nghiệm và công thức nghiệm thu gọn. Ta
Trở lại công thức nghiệm và công thức nghiệm thu gọn. Ta
đã biết:
đã biết:
N
N
ế
ế
u
u


t

t
í
í
c
c
h
h


a
a
c
c


<
<


0
0


t
t
h
h
ì
ì





























d
d



ơ
ơ
n
n
g
g


h
h
a
a
y
y


â
â
m
m
?
?


V
V
ì
ì



s
s
a
a
o
o
?
?

2. Dạng 2: Không giải phơng trình, xét số nghiệm của
nó.
Bài 22 SGK/49. Không giải phơng trình, hãy cho biết mỗi
phơng trình sau có bao nhiêu nghiệm:
018907
5
19
b) ;02005415 )
22
=+=+
xxxxa
Đ.A:
Đ.A:
a)
a)
Vì a.c = 15.(-2005) < 0 nên phơng trình có hai nghiệm
Vì a.c = 15.(-2005) < 0 nên phơng trình có hai nghiệm
phân biệt.
phân biệt.
b) Vì a.c = (-19/5).1890 < 0 nên phơng trình có hai

b) Vì a.c = (-19/5).1890 < 0 nên phơng trình có hai
nghiệm phân biệt.
nghiệm phân biệt.
Ghi nhớ:
Ghi nhớ:
N
N
ế
ế
u
u


p
p
h
h


ơ
ơ
n
n
g
g


t
t
r

r
ì
ì
n
n
h
h


b
b
ậ
ậ
c
c


h
h
a
a
i
i






















































c
c
ó
ó


a
a
c
c
<
<
0
0



t
t
h
h
ì
ì


n
n
ó
ó


c
c
ó
ó


h
h
a
a
i
i


n

n
g
g
h
h
i
i
ệ
ệ
m
m


t
t
r
r
á
á
i
i


d
d
ấ
ấ
u
u


Bài 24 SGK/50.
Cho phơng trình( ẩn x)
0)1(2
22
=+
mxmx
,

a) Tính
b) Với giá trị nào của m thì phơng trình có hai nghiệm
phân biệt? Có nghiệm kép? Vô nghiệm?
3. Dạng 3: Tìm điều kiện để phơng trình có nghiệm
3. Dạng 3: Tìm điều kiện để phơng trình có nghiệm
H.D:
H.D:
Hãy xác định hệ số a, b, c của phơng trình.
Hãy xác định hệ số a, b, c của phơng trình.
Đ.A:
Đ.A:
a = 1; b = -(m 1); c =
a = 1; b = -(m 1); c =
2
m
Hãy tính
Hãy tính
,


' 0
∆ =

' 0
∆ >
[ ]
2
2
2 2
) ' ( 1) 1.
2 1
1 2 .
a m m
m m m
m
∆ = − − −
= − + −
= −
Bµi 24 SGK/50
Bµi 24 SGK/50
.
.
b) Ph¬ng tr×nh cã hai nghiÖm ph©n biÖt khi nµo?
b) Ph¬ng tr×nh cã hai nghiÖm ph©n biÖt khi nµo?
Ph¬ng tr×nh cã nghiÖm kÐp khi nµo?
Ph¬ng tr×nh cã nghiÖm kÐp khi nµo?
Ph¬ng tr×nh v« nghiÖm khi nµo?
Ph¬ng tr×nh v« nghiÖm khi nµo?
' 0
∆ <

§¸p
¸n:

1
' 0 1 2 0 2 1
2
m m m
∆ > ⇔ − > ⇔ − > − ⇔ <
1
' 0 1 2 0 2 1
2
m m m
∆ < ⇔ − < ⇔ − < − ⇔ >
•
Ph¬ng tr×nh cã hai nghiÖm ph©n biÖt khi
Ph¬ng tr×nh cã hai nghiÖm ph©n biÖt khi
•
Ph¬ng tr×nh cã nghiÖm kÐp khi
Ph¬ng tr×nh cã nghiÖm kÐp khi
•
Ph¬ng tr×nh v« nghiÖm khi
Ph¬ng tr×nh v« nghiÖm khi
' 0∆ =
' 0∆ >
' 0
∆ <
1
' 0 1 2 0 2 1
2
m m m
∆ = ⇔ − = ⇔ − = − ⇔ =

Từ Bài 24 SGK/50 ta có bài toán sau:

Bài 1: Giải và biện luận phơng trình( ẩn x)
theo tham số m
0)1(2
22
=+
mxmx
Bài 2: Tìm m để phơng trình( ẩn x)
có hai nghiệm trái
dấu.
2
( 1) 2( 1) 3 0m x m x
+ =
Nếu thay đổi hệ số của phơng trình ta còn có thể đa ra
Nếu thay đổi hệ số của phơng trình ta còn có thể đa ra
đợc nhiều dài tập khác. Các em tiếp tục khai thác nhé!
đợc nhiều dài tập khác. Các em tiếp tục khai thác nhé!

Bài 23 SGK/50. Ra đa của một máy bay trực thăng theo
dõi chuyển động của một ô tô trong 10 phút, phát hiện
rằng vận tốc v của ô tô thay đổi phụ thuộc vào thời gian
bởi công thức:
,135303
2
+=
ttv
( t tính bằng phút, v tính bằng km/h).
( t tính bằng phút, v tính bằng km/h).
a) Tính vận tốc của ô tô khi t = 5 phút.
a) Tính vận tốc của ô tô khi t = 5 phút.
b) Tính giá trị của t khi vận tốc ô tô bằng 120 km/h

b) Tính giá trị của t khi vận tốc ô tô bằng 120 km/h
(làm tròn kết quả đến số thập phân thứ hai).
(làm tròn kết quả đến số thập phân thứ hai).
4. Dạng 4: Bài toán thực tế.
4. Dạng 4: Bài toán thực tế.
Nêu cách làm phần a) ?
Nêu cách làm phần a) ?
Nêu cách làm phần b) ?
Nêu cách làm phần b) ?
Rađa theo dõi trong bao nhiêu phút? Điều kiện của t là gì?
Rađa theo dõi trong bao nhiêu phút? Điều kiện của t là gì?

H.D: Đk:
Khi v = 120 (km/h), để tìm t ta giải phơng trình
0510135303120
22
=++=
tttt
Giải phơng trình trên xong ta cần đối chiếu giá trị
nghiệm vừa tìm với điều kiện của ẩn để trả lời.
100
<
t
Lu ý:
Lu ý:


- Phơng trình bậc hai một ẩn có rất nhiều ứng
- Phơng trình bậc hai một ẩn có rất nhiều ứng
dụng trong giải toán. Đặc biệt trong giải bài toán thực tế.

dụng trong giải toán. Đặc biệt trong giải bài toán thực tế.


- Khi g
- Khi g
iải bài toán thực tế. Giải xong, ta cần đối
iải bài toán thực tế. Giải xong, ta cần đối
chiếu giá trị nghiệm vừa tìm với điều kiện (nếu có) của
chiếu giá trị nghiệm vừa tìm với điều kiện (nếu có) của
ẩn để trả lời.
ẩn để trả lời.

III. Cñng cè:
Bµi 1: Ph¬ng tr×nh cã hai nghiÖm
tr¸i dÊu khi:
A. m = 1; B. m >1; C. m < 1; D. m = 2.
0)1(2
2
=−+−
mxx
§¸p ¸n:
§¸p ¸n:
C
C
Bµi 2: Ph¬ng tr×nh cã mét nghiÖm
x= -1. Khi ®ã gi¸ trÞ cña m lµ:
A. m = 1; B. m =2; C. m =-2; D. m = 0.
0
22
=−+

mxx
§¸p ¸n:
§¸p ¸n:
D
D

Híng dÉn häc ë nhµ:

§äc tríc bµi HÖ thøc Vi- et vµ øng dông

Làm bµi 20c,d; 21b; 23, (SGK/49,50)

Làm bµi 29; 31; 32 ; 33; 34 (sBT/42,43)