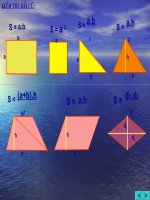
DIỆN TÍCH ĐA GIÁC
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (129.66 KB, 8 trang )
A
B
CD
Tuần 18:
Tiết 26:
Chương II: ĐA GIÁC . DIỆN TÍCH ĐA GIÁC
Bài 1: ĐA GIÁC. ĐA GIÁC ĐỀU
I/Mục tiêu:
- HS biết sử dụng phép tương tự để xây dựng khái niệm đa giác lồi,
đa giác đều, từ những khái niệm tương ứng về tứ giác.
- HS biết tính tổng số đo các góc của 1 đa giác.
- Vẽ được và nhận biết được 1 số đa giác lồi, 1 số đa giác đều.
- Biết vẽ các trục đối xứng và tâm đối xứng (nếu có) của một đa giác
đều.
- Kiên trì trong suy luận (tìm đoán và suy diễn), cẩn thận và chính xác
trong vẽ hình.
II/Phương pháp :
- Nêu vấn đề, gợi mở, khái quát.
- HS thảo luận hoạt động theo nhóm.
III/Chuẩn bị :
- GV: Thước êke, máy vi tính, máy chiếu, phấn màu, compa, bút long.
- Bài dạy điện tử, phần mềm Sketphpad, Violet.
- HS : SGK, thước êke, compa, thước đo góc.
IV/ Tiến trình dạy và học :
1.Ổn định lớp:
2.Kiểm tra bài cũ: ( 5 phút):
GV :hiển thị slide 2:
Bảng phụ
GV:Thầy có hai câu hỏi như sau:
Câu1: Điền từ thích hợp vào chỗ trống :
Tứ giác ABCD là hình gồm ………… AB,BC,CD,DA trong đó bất kỳ hai
đọan thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác lồi là tứ giác luôn nằn trong………… mặt phẳng có bờ là đường
thẳng chứa bất kỳ cạnh nào của tứ giác,
Câu 2: Trong các hình sau, hình nào là tứ giác lồi?
-Hình………… là đa giác.
-Hình………… là đa giác lồi.
GV: gọi một học sinh lên trả lời.
HS: trả lời.
GV: gọi học sinh nhận xét.
HS: nhận xét.
GV: nhận xét và ghi điểm.
1
Hình 1
Hình 2
E
F
H
G
H
ì
n
h
3
GV: Ở hình 3 không là tứ giác vì có hai đoạn thẳng cùng nằm trên một
đường thẳng.
3.Giới thiệu bài mới:
GV: chỉ hình 1,2: Những hình có nhiều cạnh như thế này và bất kì hai đoạn
thẳng nào cũng không cùng nằm trên một đường thẳng, người ta gọi những hình
như thế là đa giác. Ta sang :
Chương II: ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
Bài 1: ĐA GIÁC. ĐA GIÁC ĐỀU.
*Hoạt động 1: Khái niệm về đa giác lồi:(15 phút)
2
Hoạt động của giáo viên Hoạt động của học sinh Nội dung
Ta đi vào nghiên cứu phần
thứ nhất” Khái niệm đa giác
lồi”.
GV: Ta tìm hiểu định nghĩa
đa giác lồi. GV ghi bảng.
GVchỉ vào hình 1 slide 2:
Những hình có nhiều cạnh
và hai bất kì không cùng
nằm trên một đường thẳng
được gọi là đa giác. Tương
tự:
GV: (Hiển thị Slide 3):
Trong các hình trên, hình
nào là đa giác?.
GV: gọi học sinh nhân xét.
GV: Các hình 1, 2, 3, 4, 5, 6
là các đa giác.( Cho hiển
thị kết quả slide 4).
GV hiển thị slide 5:
GV: Tại sao ở hình 7 không
là đa giác ?.
GV: Nhận xét, hình 7
không là đa giác vì có hai
đoạn thẳng AE, ED cùng
nằm trên một đường thẳng.
(Hiển thị kiểm tra hình 7).
GV:Hiển thị Slide 6:Chia
các đa giác trên thành hai
nhóm hình: Nhóm 1: các
hình 1, 2, 3. Nhóm 2: các
hình 4, 5, 6.
GV: Sử dụng nhóm hình 1:
1,2,3 kẻ đường thẳng DE,
CD, AE khẳng định đa giác
nằm ở hai nửa mặt phẳng có
bờ là đường thẳng DE, CD,
AE.
GV: Sử dụng nhóm hình2:
4, 5, 6: Kẻ đường thẳng
chứa bất kì cạnh nào của đa
giác khẳng định: đa giác
luôn nằm trong một nửa
mặt phẳng có bờ là đường
thẳng chứa bất kì cạnh nào
của đa giác đó. Những đa
giác như vậy gọi là đa giác
lồi.
HS:Các hình 1, 2, 3, 4, 5, 6
là các đa giác.
Nhận xét.
Vì có hai đoạn thẳng AE và
ED cùng nằm trên đường
thẳng.
1.Khái niệm về đa giác :
3
Hình 1
Hình 2
Hình 3
Hình 4
Hình 5
Hình 6
B
E
D
A
C
B
Hình 7
C
B
A
E
B
C
A
D
E
C
B
A
*Hoạt động 2:Đa giác đều: (15 phút)
Hoạt động giáo viên Hoạt động học sinh Nội dung
GV: Từ các hình vẽ trên,
Em hãy cho biết: thế nào
là đa giác đều?.
GV: Kết luận, GV lặp lại.
GV: Gọi 2 học sinh khác
nhắc lại.( GV cho hiện ).
GV: (Đổi màu từng
hình): *Đa giác có 3 cạnh
bằng nhau và 3 góc bằng
nhau gọi là tam giác.(GV
hiển thị tên).
*Đa giác có bốn cạnh
bằng và bốn góc bằng
nhau gọi là tứ giác hay
còn gọi là hình vuông.
( Hiển thị tên).
*Đa giác có 5 cạnh bằng
nhau và 5 góc bằng nhau
gọi là ngũ giác đều. (
hiển thị tên ).
*Đa giác có 6 cạnh bằng
nhau và 6 góc bằng nhau
gọi là lục giác đều. (hiển
thị tên ).
GV: Thầy hướng dẫn các
em cách vẽ đa giác đều
ở hình trên: (GV vừa nói
vừa hiển thị.)
GV:Vẽ bảng:
*Đối với tam giác đều ta
làm như sau:
-Ta lấy hai điểm B và C
không trùng nhau và
không được lớn hơn bán
kính compa.
-Vẽ cung tròn tâm B bán
kính BC và vẽ cung tròn
tâm C bán kính BC. Hai
cung tròn này cắt nhau tại
một điểm ta đặt là A, nối
3 điểm A, B, C lại ta
được tam giác đều. ( vẽ kí
HS1: phát biểu
HS2: nhận xét.
Nhắc lại.
HS chú ý xem.
HS xem và vẽ
2.Đa giác dều:
a.Định nghĩa:
Đa giác đều là đa giác có tất cả
các cạnh bằng nhau và tất cả các
góc bằng nhau.
b.Cách vẽ:
*Tam giác đều:
4
hiệu bằng lên hình)
GV nói và hiển thị theo
lời nói:
*Đối với tứ giác đều ta vẽ
như sau:
-Vẽ đường tròn tâm O
bán kính tùy ý.
-Vẽ đường kính AC và
BD vuông góc với nhau
tại O, nối bốn điểm lại
với nhau ta được tứ giác
đều.
GV hiển thị slide 12:
GV: nói và hiển thị theo
lời nói:
*Đối với ngũ giác đều ta
vẽ như sau:
-Vẽ đường tròn tâm O
bán kính tùy ý.
-Vẽ bán kính OA.
-Vẽ bán kính OB sau cho
AÔB = 72
0
.
-Vẽ cung tròn tâm B bán
kính AB, cung tròn này
cắt đườn tròn tâm O tại
một điểm ta đặt là C và
chúng ta tiếp tục làm như
thế ta được 5 điểm nằm
trên đường tròn, nối các
điểm lại với nhau ta được
ngũ giác đều.
GV: Vừa nói vừa làm:
(GV vẽ bảng)
*Đối với lục giác đều ta
vẽ như sau:
-Vẽ đường tròn tâm O
bán kính tùy ý.
-Lấy điểm A nằm trên
đường tròn tâm O, vẽ
cung tròn tâm A bán kính
OA, cung tròn này cắt
đường tròn tại một điểm,
đặt là B.
-Vẽ cung tròn tâm B bán
kính OA, cung tròn này
cắt đường tròn tại một
điểm, ta đặt là C, tiếp tục
làm như thế ta được 6
điểm nằm trên đường
tròn, nối 6 điểm lại với
nhau ta được lục giác đều.
*Tứ giác đều ( hình vuông)
*Ngũ giác đều:
*Đối với lục giác đều:
5
O
A
B
C
DE
O
A
B
C
D
E
G
A
B
(vẽ kí hiệu bằng nhau.)
GV: Xác định trục đối
xứng của đa giác đều:
GV: Thời gian thảo luận
là 4 phút.
GV:( hứơng dẫn nhóm
không làm được).
GV: Thu bài và cho nhóm
nhận xét chéo.
GV: Hiển thị kết quả ở
các slide 13, 14, 15, 16.
GV: Em hãy so sánh số
cạnh và số trụ đối xứng
của đa giác đều?.
GV:Kết luận. vậy nếu đa
giác đều có bao nhiêu
cạnh thì có bấy nhiêu trụ
đối xứng.
GV: để hiểu rõ về mối
liện hệ giữa các cạnh,
đường chéo và các góc đa
giác, ta làm bài tập sau:
GV: hiển thị slide 17
HS: hợp tác nhóm
Nhóm 1: Gấp hình xác
định trục đối xứng của
tam giác đều.
Nhóm 2: gấp hình đối
xứng của tứ giác đều.
Nhóm 3 gấp hình đối
xứng của ngũ giác đều.
Nhóm 4: Gấp hình đối
xứng của lục giác đều.
( có hướng dẫn của GV)
HS: quan sát màn hình.
HS1: trả lờ.
HS 2: nhận xét
*Hoạt động 3: xây dựng công thức tính tổng các góc của đa giác.( 7 phút)
Hoạt động giáo viên Hoạt động học sinh Nội dung
Đa giác
n cạnh
Số cạnh
4
Số đường chéo xuất phát từ một
đỉnh 2
Số tam giác được tạo thành
4
Tổng số đo các góc của đa giác. 4.180
0
=
720
0
GV:Số cạnh của tứ giác là 4.
GV: Số đường chéo xuất phát
từ một đỉnh của tứ giác là mấy?
GV: Nhận xét và hiển thị. Số tam giác
được tạo thành là bao nhiêu?
GV: nhận xét và hiển thị. Tổng
số các góc của đa giác là bao
HS: quan sát.
HS: 1
HS: 2
HS: 2.180
0
= 360
0
6
nhiêu?
GV: Nhận xét và hiển thị.
GV:Số cạnh của ngũ giác là
bao nhiêu?
GV: nhận xét và hiển thị. Số
tam giác được tạo thành là bao
nhiêu?.
GV: Nhận xét và hiển thị. Tổng
số đo các góc của ngũ giác là
bao nhiêu?.
GV: Làm tương tự như vậy đối
với lục giác và đa giác n cạnh.
(Nếu HS không trả lời được đối
với đa giác n cạnh thì GV
hướng dẫn)
GV:Từ bảng trên ta rút ra được
Công thức tính tổng số đo các
Góc của đa giác n cạnh là:
(n -2 ).180
0.
GV: Ghi công thức lên bảng.
GV: hiển thị slide 18
GV: Áp dụng công thức trên các
em làm bài tập sau: Tính tổng
số đo các góc của hình 7 cạnh,
9- cạnh.
GV: kết luận và hiển thị kết quả.
GV: Phần học lý thuyết đến đây
là hết.
HS: 5
HS:3
HS:3.180
0
= 480
0
HS: trả lời
HS1,2: giải.
HS3,4: nhận xét.
*Công thức tính tổng số
đo các góc của đa giác
n cạnh:
(n – 2).180
0
với n
≥
3
Ví dụ:Tính tổng số đo
các góc của hình 7 cạnh
9-cạnh
Giải:
Với n = 7:
(7 – 2).180
0
= 900
0
Với n = 9:
( 9 – 2) . 180
0
= 1260
0
*Hoạt động 4: củng cố: (3 phút)
Hoạt động của giáo viên Hoạt động của học sinh Nội dung
GV:Em hãy nhắc lại định nghĩa
Đa giác lồi, đa giác đều.
Về nhà các em làm bài tập 1,2,
3,5 trang 115 SGK.
GV: hiện slide 19
GV: hướng dẫn bài tập 5/115
SGK:
-ngũ giác đều là hình có năm
cạnh ta dựa vào công thức
tính tổng các góc đa giác
n - cạnh ta sẽ tính được tổng
số đo các góc của nó.(GV
hiển thị thị cách tính.)
vậy để tính số đo của một góc
ta lấy tổng số đo các góc của
nó chia cho 5 (GV hiể thị cách
HS1,2: trả lời.
HS lắng nghe.
HS: quan sát và nghe.
7
tính)
tương tự các đa giác đều còn lại.
*GV: Nhận xét tiết học.
8