Bài Báo Cáo Số 1 Chương 1 Ứng Dụng Matlab Trong Mô Tả Toán Học Hệ Thống.pdf
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (290.99 KB, 10 trang )
BỘ GIÁO DỤC & ĐÀO TẠO
TRƯỜNG ĐẠI HỌC SƯ PHẠM KỸ THUẬT TP. HỒ CHÍ
MINH
KHOA ĐIỆN – ĐIỆN TỬ
BỘ MƠN TỰ ĐỘNG ĐIỀU KHIỂN
-----------------⸙∆⸙-----------------
BÀI BÁO CÁO SỐ 1
CHƯƠNG 1: ỨNG DỤNG MATLAB TRONG
MƠ TẢ TỐN HỌC HỆ THỐNG
GVHD: NGUYỄN PHONG LƯU
SVTH: NGUYỄN TẤN TÀI
MSSV: 19151282
Tp. Hồ Chí Minh, tháng 2 năm 2022
YÊU CẦU THỰC HIỆN
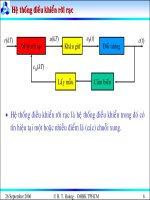
1.3.1 Hãy tìm hàm truyền của hệ thống có sơ đồ ở hình 1.1 và hình 1.2.
a. Tính tốn bằng lý thuyết.
b. Sử dụng các hàm trong matlab.
Các hàm truyền được định nghĩa như sau:
𝐺1 = 5; 𝐺3 = 𝐺5 = 𝑠; 𝐺6 = 𝑠 + 2; 𝐻1 = 1; 𝐺2 ¿ G4 =
1
3
1
; H 3=
; H 2= .
s+1
1+4 s
s
Hình 1.1 Sơ đồ khối 1
BÀI LÀM:
Hình 1.1:
a. Tính tốn bằng lý thuyết.
Khối G1 song song với khối G3: G1G3 = G1 + G3
Khối G2 và H1 là khối hồi tiếp âm:
G2H1 =
Khối G1G3 nối tiếp với khối G2H1:
G1G3G2H1 = (G1 + G3).
Khối G1G3G2H1 là khối hồi tiếp âm đơn vị.
Ta có hàm truyền của hệ thống là:
G(s) =
2
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
Thay các hàm đã được định nghĩa vào hàm truyền , ta được:
G1(s) =
b. Sử dụng các hàm trong matlab.
Nhận xét:Kết quả hàm truyền khi tính bằng lý thuyết giống với khi tính bằng
MATLAB.
Hình 1.2:
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
(1)
(2)
Hình 1.2 Sơ đồ khối 2
Các hàm truyền được định nghĩa như sau:
1
3
1
𝐺1 = 5; 𝐺3 = 𝐺5 = 𝑠; 𝐺6 = 𝑠 + 2; 𝐻1 = 1; 𝐺2 ¿ G 4 = s+1 ; H 3= 1+4 s ; H 2= s .
a. Tính tốn bằng lý thuyết.
Ta chuyển bộ tổng số (1) ra sau khối G4.
Gộp bộ tổng số (1) vừa chuyển với bộ tổng số (2).
Khối G3 nối tiếp với G4, khối G4 nối tiếp với H3:
G3G4 = G3.G4
G4H3 = G4.H3
Khối G3G4 song song với khối G6:
G3G4G6 = G3.G4 + G6
Khối hồi tiếp âm G5 và G4H3:
G4G5H3 =
Khối G2 nối tiếp với G3G4G6 nối tiếp với G4G5H3:
G2G3G4G5G6H3 = G2.(G3.G4 + G6).(
)
Khối hồi tiếp âm G2G3G4G5G6H3 và H2:
G2G3G4G5G6H3H2 =
Khối G1 nối tiếp với G2G3G4G5G6H3H2:
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
G1G2G3G4G5G6H3H2 =
Khối hồi tiếp âm G1G2G3G4G5G6H3H2 và khối H1, nên ta được hàm truyền của
hệ thống như sau:
G(s) =
Thay các hàm vào hàm truyền , ta được:
G2(s) =
b. Sử dụng các hàm trong matlab.
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
Nhận xét: Kết quả hàm truyền khi tính bằng lý thuyết giống với khi tính bằng
MATLAB khi chưa rút gọn. Khi rút gọn đơn gản biểu thức sẽ hạ số bậc ở tử
và mẫu của hàm truyền.
1.3.2 Biểu diễn các hàm truyền trên bằng hệ phương trình biến trạng thái.
a. Biến đổi hàm truyền trên về hệ phương trình biến trạng thái bằng lý thuyết.
b. Dùng các hàm trong matlab để thực hiện biến đổi trên.
BÀI LÀM:
Tính tốn bằng lý thuyết.
- Hình 1.1:
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
Ta có: G1(s) =
Chuyển về phương trình vi phân, ta được:
Ta có: hệ phương trình biến trạng thái là:
- Với hình 1.2:
Ta có:
Chuyển về phương trình vi phân, ta được:
Ta có: hệ phương trình biến trạng thái là:
Với:
,
,D=1
a. Sử dụng các hàm trong matlab.
Với hình 1.1:Dùng lệnh state space với cú pháp: pttt=ss(g)
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
Với hình 1.2:Dùng lệnh state space với cú pháp: pttt=ss(g)
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
Nhận xét: Kết quả hàm truyền khi tính bằng lý thuyết giống với khi tính bằng
MATLAB.
TÀI LIỆU THAM KHẢO
- “Lý thuyết Điều khiển tự động”, Nguyễn Thị Phương Hà, Huỳnh
Thái Hoàng, NXB ĐHQG TPHCM.
- “Bài giảng Điều khiển tự động”, Nguyễn Thế Hùng.
- “MATLAB for Control System Engineers” Rao V Dukkipati.
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG
BAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONGBAI.bao.cao.so.1.CHUONG.1.UNG.DUNG.MATLAB.TRONG.mo.ta.TOAN.hoc.he.THONG