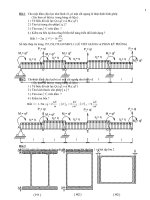
Hướng dẫn giải bài tập lớn sức bền vật liệu (tái bản) đinh trọng bằng
Bạn đang xem bản rút gọn của tài liệu. Xem và tải ngay bản đầy đủ của tài liệu tại đây (7.94 MB, 96 trang )
TRƯỜNG ĐẠI HỌC KIÊN TRÚC HÀ NỘI
ĐINH TRỌNG BẰNG
- HƯỚNG DẪN BIẢI BÀI TẬP LỨN
SUC BEN VAT LIEU
(Tai ban)
NHA XUAT BAN XAY DUNG
HA NOI - 2008
LOI NOI DAU
Dé phuc vu cho hoc vinh học tập môn Sức bén vat liéu, nhat la thie hién lam cac bat
tập lớn được thuận tiện, chúng tôi biên soạn tài liệu “Hướng ddan giải bài tập lớn
SUC BEN VẬT LIỆU”. Sách gơm 2 phần chính:
1. Phần bài giai mau các loại sơ đồ của 5 bài tập lớn:
+ Bai tap lớn số Ì: Về biểu đơ nội lực (cho thanh và khung phẳng) (4 sơ đồi).
+ Bài tập lớn số 2: Đặc trưng hình học của hình phẳng (2 sơ đồi).
+ Bài tập lớn số 3: Tính dâm thép (2 sơ đơ).
+ Bài tập lớn số 4: Tính đâm trên nên đàn hồi (1 xơ đồ).
+ Bài tập lớn số Š: Tính cột chịu nén (2 sơ dé).
2. Phan bai tép lớn để học sinh tự giải.
Ngồi ra cịn có phần phụ lục gồm các bang tra:
- Bảng tra đặc trưng hình học của thép định hình I, [, £;
- Bảng tra giá trị của các làm Crulốp: A,B.C,
ÐD.
Tời liệu này được biên soạn lần đâu nên không thể tránh khỏi những thiếu sót. Mong
các bạn đọc góp ý phê bình.
Tác giả
PHAN
ay NAA
BATT apP GIẢI MẪU
BA! TAP LON SO 1
VE BIEU PO NOI LUC
_ SƠ ĐỒ A; Vẽ các biểu đỏ nội lực cho đầm chịu lực như hình 1.Šä băng phương pháp gia tích. -
Sốliệu
a=2m;
k, = 0,5:
P,=I5kN;
Bài giải:
k, = 1,5:
P,=20kN;
q=8kN/m.
M, = 10 kNm;
|
M, = 20 kNm.
|
1) Xác định phán lực liên két va chia doan:
* Từ điều kiện cân bằng của dầm AB (hình I.Š5a) ta có:
mạ
= 3a Vụ =
=v.-T
Bal
= I
3.2
qa x1 5%
|
|
2aP
+M,—M,+P;a=0
4qa” _Sqa” +2P,a—-M, +M,
30
24 |
—P,a
cưng
4.8.2
3
2
2
_ 98.2
24
2,Y= Vụ — Vụ —P, --P) =
Kiém
——
|
+ 2.15.2
-—10+ 20—20.2
|
}=11kN
I qa_g
qa
24
8.2
=> V, =P, +P, +2 Ác TT = VẠ. =15+20+`-8.2~'“~11=30kN
2”
8
2
8
|
tra lại:
|
=3aV,+M,+—-
| 2m
ne:
|
qa
4
—
—--—
4
3
1
2°
qa
“_p,
3
a-—M,
+4aP,=
= 30.3.2+ 20+ 82 42 5212_ 15.2 -10- 20.4.2 =0
8
3
2
3
* Chia đoạn: Dựa vào tải trọng tác dụng trên dầm tachia dầm thành 4 đoạn: AC= (1);
A
CD = (2); DB = (3); BE = (4).
2) Thiết lập các biểu thức nội lực ở mỗi đoạn dầm:
pe
Doun | (hinh 1.1): Ding mat cat 1-1 e AC và xét
can bang phần trái dầm ta có:
qị=
a—-Z,
3 _:q=4(2-z4)
|
|
|
-= qz,-=4z
Qi
y = VyA SÁU
¬.
2
A
—
—
|
ye
|
|Va=fKN
|
|
Hình LJ
-
Po
M,
>
¬
4
fa"
|
Đá
SOT
MO
AS
at
M??=V,;
TT
TT
`
ng:
¬„
-SếL
c
“ấi
2
3
SZ,
x
di;
Zi
2
3
¬3
22;(2-2,)
=ÍlZ=-s*=
ở
hs
3
3
= 1 (227 -12z, + 33)
3
3
Qy)
= 227 -8z, +11
{1}
=> (l) 4 -
iM.
|
Với (0 <7,
(0 _ ft py 2
12 +33)
33
= — (274 =l27,
cơ]
< 2m)
St
ee ee
ete
Men
Ae
am a
|
9
có 6 babề 16,
lõm
Q,
Qy
—2 —-=4>0
?
quay lên trên vì:
|
dzˆ
MỸ” có bề lõm quay lên trên vì:
Tai z, = O thi QV (0) = 1IkN:
?n4(D
5 ”— =q(Z)<0
.
Qi (2) = 3KN = Qin
Mt"(0=0
) ;
.
:
dZ~
trong doan AC vi q,(z) = 0
M\"(2) = = kNm
Đoạn 2 (hình 7.2): Dùng mặt cắt 2-2 € CD và xét cân bằng phần trái dầm ta có:
q>
Z,—-2
I=
Sy
(2)
—
=V,
q
1
2
—
=4
“a
„—
Z›—2
2)
q›;(Z; -a)
—-P,| -2-qa 4222
0°"
A2
2
= 1-15-52 429)
.
MØ =v,;,_%8
x
A”
2
2
(
4
„—2)ˆ
¬—-..
2
|
=llz, -s[ 2, -)-
3)
1(
=2, ~2)? ~12
2,-2
2
.
)
2
4 A2(Z2 =a)”
6
|
I3(z, — 2) +502; ~2)° = | 5 Re, ~2)° — 36z, + 106]
P,= 15kN
2
(2)
M
Hình L2
Ĩ;
‡
|
q,
\ D
ị
l
+
Im
Z,
°
2
x
(2)
y
q/2
|MỆT
= a 2 (2, 2
ì
[
3
= 362, + 108]
r
|
ae
Q2) = -12RN = Q,,,. trong doan CD ; Q\’'(3) = -10KN
| MẸ}'2)==—
34
kìm ;
_
ˆ
M
Đoạn 3 (hình Ƒ.3)- Dùng mặt cắt 3-3 € DB. Và xét cần bằng phản phải đầm ta có:
QỆ”=P; —Vạẹ =20— 30 =—I0kN
MẸ” =M; +V;(z,~2)— P›z,= 20+ 30 (z, — 2) — 20,
=
8
x
|
10z, - 40
da
P;=20 kN
M,=20kNm
LZ
O;
†
|
m3
y
]
E
O,
|
|
.
{
| Va=30kN
2m
0|
4
|
sự,
y
Hinh L3
(3)
|
P;= 20kN
|
"5
24
=
“44
M, 4
|
Hình 1.4
Qÿ” =—I0kN
Với (2
Me = 10z, —40
Qy(2)= QY(5) = -10;
MẸ?(2) =~20 ; M?(5) =I0
Đoạn 4 (hình 1.4): Dùng mặt cắt 4-4 6 BE và xét cân bằng phần phải dầm ta có:
Q1 = 20kN
x
TS
đ)Z“2y —
4MZ
Với (Ú
Mf?(0y=0;. M2) = -40kNm
3) Vẽ biểu đồ:
Dựa
vào các biếu thức của Q,. M, trong cac doan (1), (2), (3), (4) ta sẽ được các biều
@))
(hình I.5b, c).
Chú ý: Ở đây ngoại lực vng góc với trục dầm — N, = OVz.
a)
ye TSK
2
|
>
|
`.„
⁄
-
2
i
k,a=3m
mM
|
|
“M;=30kN
8
|
2
.
Sn
?
/
`
k;a=Ím
J
\
|
ane >
-
M1,=13&kNm
.
|2
Ƒ
- Ps=20kM
sous
F 17 TOKN
3
3
|
|
2
b)
| |
+
Tt
ae eR
NMA AER, SR
CARR - “93
VheoyssigEsivtas.>
<“h
ni
TM
ey
3
TTT
11,3
10
Hình 1.5
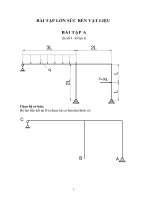
SO DO B: Hay vé cic biéu dé ndi lực cho khung phang, chiu luc như hình
I.I0a bang
phuong phap giai tich.
Số liệu:
a= 3m:
P,=
IOkN;
k,=1,5;
2
KT:
P›= I2kN;
M, = 15 kNm
|
q= 6km :
;
M, = 10 kNm.
Bài giải:
1) Xác dinh phan luc va chia doan:
Ở đây A là ngàm, E là đầu tự do nên tá không cần xác dịnh phan lực Á.
_- Ta chia khung thành 4 đoạn I, 2, 3, 4 như hình ve.
2) Thiết lập các biểu thức nội lục ở môi đoạn khung:
Doan I (hinh 1.6): Dang mat cat 1-1 € AE và xét cân
bằng phần dướ: khung ta có:
Qh
IN,
|
48,
3
q
3°!
=0
|
18
1)
đ2425213
— |
L
M, =>
2
|
5,
4,
Hinh 1.6
2)732
=—-Z,
4
2; “t=~=2i
3
9
Voi (0
}P;=12kN
Đoạn 2 (hình 1.7): Ding mat cat 2-2 cOD và xét cân
bằng phần phải khung ta có:
N,
=—-—
]
3g=-——:
7a d2
N;
|
\
|
8.3=-I2kN
é
0,
,
KN
MU
[to
0,1
3m
E
2
Hinh 1.7
_Với(0
Đoạn 3 (hình !.8): Dùng mặt cắt 3-3 € BC và xét cân
. bằng phần khung phía trên ta có:
(N,=-P, =-l2kN.
Sa
8.3
8.3
= P, -— = 10-— =-2kN
HT
2
|
M,=15kNm
|
Py=tOKN
‘day
¢ \/
:
0;
=_—
|
3
N
—k
- 1) = 223-31
15=10z, -10-24+ 12(z,
/
3m
3
|
_ Hình L8
(=
kN
f 40 978m
| 2m
M. TQ,
Ệ
P„=12kN
M;=[l0kNm
Voi
(0 <2, <3).
E
1
M,(0)
(ht„h
-31kKNm
Poun
‹Í
i
Dùng
miất cắt 4-4
; M3)
= - 25 kNm.
8),
|
© =10KN
Mor Skin
P2=12kN
M;= 10KNtri
|
_„=8).
kN
#
————_——
=P,
[N
(4)
c AB
:
=
và xét can
baneot phan
trên
townt
la CÓ:
_ sey
ii
= -12 KIN
|
Q,=P,- = 3 -qz, =-2-8z,
—
M,
= M,
.
`
—M,;,
—ĐŒ,
—P, 242,
_
+3)—
+2)+ 74
2
2
~
247?
+2z, —25
~
- Với (
Q,(0)=-2kN; —
N,
|
Q/(1,5)=-14kN;
M,(0)=25kNm;
M,(1,5)=-
Hinh 1.9
13 kNm.
3) Về biểu đồ: Dựa vào các hệ thức (1) + (4) ta vẽ được các biểu đồ như hình
1.10.
P,=12kN
q
M.=15kNm.
P;=10kĐN
M,
kạa= 2m
E
c5
HGi)
k;a= 4,5m
8)
b)
d)
Hinh 1.10
4) Kiem tra sucan bằng cua cde Hút:
- Tách cúc nút € và D ra thỏi khu nơ bảng các mặt cát sát nút và đặt các — sai hức, nội
[.]]).
ia
luc tac dung vao cac rut
eet
C va D déu can bang.
2N1a
46kNm
M,=10kNm
7 Z}
"
12kKN
ẹẹ
P,=10kN
rom
ten
|
|
M,=15kNm r
|
jW
0 YY
|
`ơ
2ttNm
12kN
12kNm
Hinh 1.12
YHỡnh 1.11
Y=12-12=0
Z=10+2-12=0
me =15-46+31=0
_
|
â
Y=l2-l12=0
Z=l2-12=0.
im, = -10-12+22=0
S C: Vẽ các biểu đồ nội lực cho thanh chịu lực như hình I.13a bằng phương
pháp vẽ theo các điểm đặc biệt.
| = a=3m;
'
So lieu:
Bai giai:
q =8 kNĐ/m;
M, =20kNm;
P,=8kN;
P,=l10kN;
|
2
ky =F
¬:
|
M,= 14kNm.
I) Xac dinh phan luc va chia dean:
Tir diéu kién can bang của toàn thanh
Ym,
|
l.¡3a):
-q-3-10—-M, +4q-4+ P, .2+M; —0.V, =0
= P,.12+
=5 (10.12 + ~-8-30- 20+ 16-8 +8-2 +14) = 42kN
=
> m, = V_.9 + Py. 345
=> VẸ =g
2 q-3-4.q —P,
Chia 4 doan: AB, BC, CD, DE.
| (AB):
84+8.7- 14) = 20KN
1
>» Y = Vụ +Vẹ —P,
2) Vẽ biểu đồ:
-q:3-1—-M, —4q-5-P,-7+M, =0
(-10.3-—-8.3+ 20+ 20
Kiểm tra lai:
Doan
AE ta có (hình
|
0
= 42+20-10--8.3-48-8
=0
"
gy
P8:
i
?
:
ay
“
a
Pa 7
.
V
a?
rạng
ff
Ov: fa thay ———z—=---—=~ Ng 0= Hê
a
GZ
dz
|
|
|
|
quay
Q@'””
pete? xuống 8 dướirae
y
Cone).
yy
¬
‘ys
ge re
om
bai A(z
Xét
a
—
ˆ
ope
duong
cua
lõm
|
cong
^
I.
|
a
Tại z= 3m => Qig =—P, ~s.gri3= =10= 28:3 <=22 KN
diễn
:
_|
|
in
tn
có cực trị (vì qg(0) = 0) và Oya = —P,op = -LOKN
=0)> Qy-
-
oe
biéu
(a)
SỐ
|
(b)
on
Parl
dˆMP”
s
——
Xét MẸ “
¬
`
si.
"(1)
⁄
=q(z) <0 = Bề lõm của5 đường
cong biểu
diễn MỸ''hướng
lên^ trên,
dz~
Mặt khác trong đoan này QV
=
|
”
khơng cát đường chuẩn nên
`
a
3
`
F
ˆ
|
=>
M° ' khong có cực trị.
Ỉ
A
4
.
:
Tại z =0 > Mƒ”(0)=0.
P,=BkN
||
3
P+=10kN
A
=
M,=20kNm
@
B
⁄
|
Lị
@
C
Vg=42k
a=
thtt!
6
|.
3m
{
kạa = 4m Ì |
a=3m
C
D
E
Ì
kạa=4m
Ve=20kN
|
i
|
|
T
-
aa (ais)
>
NL.
7
38
2Z
“Z5
Vt
Z>
@
“22
ay
M,=14kNm
|
|
20
c)
|
Hinh 1.13
|
s.
Tại 2z = 3 =>
1
`
MU’ (3) =-PpP 3-
.
Đoạn 2- g2) = q = const > QY
*
Xét
,
(
.
¬
‘
= const;
Q (từ trái qua phải): Tại B có lực tập trung Vụ= 42kN, hướng đi lên. Vậy
- điểm b đặt bc (về phía trên) có bc= 42. Từ c kẻ cả // đường chuẩn ta được
từ
Q.0)
Xét MÍ?)(từ trái qua phải): Tại B có mơmen tập trung M¡ = 20 kNm quay thuận chiều
kim đồng hồ = ở đây biểu đồ M„ có bước nhảy đi xuống= MỊ. vậy từ Dị
dat b,c,= 20
về phía dưới được diém c,.
Tìm điểm d,: Dùng mặt cắt tại C và sét phân
trái ta CÓ:
Mỹ =423+20~10.6= 2 -8:3:4
= 38 kNm `
Nối c¡ và đ, ta được (M{?)).
Doan
4: q(z)=0>
Q\” = const;
Mé* = bac 1.
Vẽ
Q\”:
Tu e - (trén duong chuẩn) dat doan
đường chuẩn.
Vẽ MỸ”: Tại E có đặt M;=
eg= V, = 20 về phía dưới. Kẻ
gh //
= 14 về phía dưới. (Vì xét từ
oF
14 kNm => đặt đoạn e,b,
phải qua trái M; quay ngược chiều kim đồng hồ => bước nhảy đi xuống). Tìm điểm h;:
Dùng mặt cắt tại D và xét phần phải —>
MP =M;, + V,.2 = 14+ 20.2 = 54kNm
Nối g¡ và h, ta được MÍ?”.
Doun 3: 4(Z)=q =const
> Q\ =
bac 1.
Mỹ”= bậc 2
Vẽ Q8 ': Tại C không có lực tập trung —> Qi? = 20kN (ứng với điểm đầu đoạn là d).
Tại D.có lực P,= 8kN đi xuống nên để tìm điểm cuối đoạn của đường biểu diễn đồ thi
thì từ h dat hh' = P,= 8kN vé phía trên nối dh' ta được QẺ`.’ Ta thay QU ' cắt đường
chuẩn tại O'. Ta có AO@d'd~AO@'h'h:
"1`"...
Vẽ MỸ”:
dM:`
¬
zˆ
`..
=q(0) > bể lõm dường cong quay về phía trên.
|
Tại C và D khơng có mơmen tập trung nên điểm đầu và cuối của M¿
là d,h¡.
ở đoạn này vân
|
13
m-
.
3}
Tại G thì Q!'”Y =0
=> MV_
(3)
+
a
`
~
ce
Le
xá
có cực trị. Dùng
mặt cất tạient Gft vàON xét
phần phảiae thanh ta có:⁄,
>
- >
My =M, +V,..35--P,.1.5—q. “2- = 1442035-815~-8.
Lo
“j
_
=
63KN;
Hy
nw
Dat 0, 1, = 63. Noi dji,;h,
thanh dudng cong c6 bé 16m hướn g vé trén va tiép tuyén tai
I¡ song song với đường chuẩn => MỊ”.
`
-
Lểm
`
a
3
|
|
Số liệu:
a=Im:
k, = 1;
P.=l0kN;
k
P;=20kN;
=2;
q=
M,=20kNm;
Bài giải:
1) Xác định phản lực và chia đoan:
—
t‹2
SO DO D: Vẽ các biểu đồ nội lực cho thanh cong phẳng chịu lực như hình I.lóa.
I0 kN/m;
M,=45kNm.
Từ điều kiện cân bằng của thanh AB (hình I.lóa) ta có:
#Pz=qI-H¿=0=H,=l0N -
Xmạ = Vụ.2 = g.1.0,5 ~ Mỹ + Ms — Pị.l — q.2.3 ~ P.4 =0
=>
V, =~
(10.0,5 + 20-45+
10+
10.6 + 20.
= 4)
65kKN.
2 mg = Vq.
—2
Hy.1 +q.1.0,5- M, +M,+P, .1 - q.2.1 — P,.2=0
)
Ì
V,z = 5 (10 — 10.0,5 + 20 - 45 — 10 + 10.2 + 20.2) = IS kN
>
Kiểm tra lai: ©
|
|
SY =-V,- P+ V,- q.2.- P,=-15- 10 + 65 - 10.2- 20 =0
Chia thanh ra 4 doan: AC, CD, BD, BE.
2) Thiết lập các biểu thức nói lực ở các đoạn
- Đoạn
I(hinh
1.14): Dùng
bảng phần dưới ta có:
mặt cát
I-|
€
thanh:
(l) và xét cân
|
_
|
(1)
_
|
(1)
Qi”
=H,
—q.Z,
1
= I0(I -Z,)
Với
(O
Zz, =O=> Nf) =15:
—
() oye.
z;=1>N
=15;
l4
7
H,=10KN
——
Qÿ'=10; Mt? =0
(Ù)
Q\?=0; qe Mi) ng) =5
-
kN
q=10-m0
2) mm.—=L
-
2
M,’ =H,.z, -q.27
= 52z,(2-z,)
?/2|
:
M,
ah”
vy
_ cm.
==
3
N\) = Vy =15kN
,
>
AU
V,=15KN
-
|
|
Hình 1.14
|
`
bang phan duct ta co:
N,
(1)
_\
vo
-
x
¬>
_
|
c
ụ
GUỚNN
2
M,=20kNm
= V, cosg, +H, sing, —q.!.sing,
Ny
Lo
_
€ (2) va xét can
Đốn 2 (hình 1.15}. Gung mat cat 2-2
|
\
2
đua
iN
WN
h
a
y
[Scose, + 10sing, —10sing, = I5cos0
Q\”
=-V, sing, +H, cos@, —q.1.cos@,
=—l5sm0
+10cos@, —10cos@,
MỸ" =V„(1—lcos@,)—H„(I+Ì
a
im
=~-I]5sing,
sing, )
+ q.1(0/5+1.sinp,)—M,~
“Ƒ
|
__—
He 106
Vạ=15kN
Hìnhl13
__ =l5(I—cos@,}— 10(1 + sin @,) + 10(0,5+ sing, )— 20 = -15cos@, — 10
a)
M,=20kNm
k,a=1m
b)
Hinh
1.16
15
eh
RE
NEE
IRE Be
-
HN
eae
-
A
LA
Es A
A
Re
Oe
HH su
ni...
eee
SH
hư
on
hú
TY
EN
ER EE
€)
4)
Hinh 1.16 (tiép theo)
NỈ}? =l5cos0,
=> (2)
Qy’
My
=—l5sino,
_—
Với
(0 <@,< 909)
= -(l5coso, + 10)
9, =0°>N,=15;Q,=0;M, =-25
9,
= 30°
>
N,
= 13;
Q,=-7,5;M,=-23
9, =45°
> N, = 10,6;
Q, =- 10,6;
M, =- 206
Y, = 80° >N, =7,5;Q,=- 13; M, =- 17,5
ø¡.=90”—=N,=0; ;Q/¿=-15;M,=- 10
Đoạn 3 (hình 1. 17): Dùng mat cat 3-3 € (3) và
xét cân bằng phần phải ta có:
Ni) =-V,.cos@, +P,.cos@, + d. 2 cos,
7
`
MI
z
2Q,
(3)
qzi0
3 1°
= (-65 + 20 + 10.2) cose~,= — 25coso,
Qý”=-V g.Sin0› +P, sin@, +q.2sing,
= (-65 + 20 + 10.2) sine, = -25sin
g,
ÌV;=§5kN
Hinh
2m
1.17
|
.
|Pz=12kN
:
h4 tớ -< =M H` GÌ =I cos@s„}+tq.2 - [.cos0¿)+ P,(S—1.cos@; )
—==650 = sosy) + 20/2 ~ cos¿ + 203 — cos0x) = 254-2)
(3)
(3
=>(3)
^
;
TN
¬—
Nợ
=
rs
OY
oma
|
ry f
¬ $8
Với 0 <0; < 90”
:
= —Z5s51n —);
MỸ” = 354 25cosep,
|
Dy
—
|
Ni"
| Q\”
21,7
0
-12,5
60
-17,7
-17,7
52,7
(
-25
45
30,
56,7
47,5
35
-21/7
_-25
-12,5
0
60
90.
My
- Đoạn 4 (hình †.!8): Dùng mặt cắt 4-4 € (4) và xét cân bằng phần phải ta có:
N?”?=0
= (4)
Qy” =P, +q.z,
Mt
|
= ~(Pyz4 +q 4 = ~524(4 +24)
Với (0 < z¿ < 2m).
_
4) 1.
z¿=0>aN,
=0;
Z,=2>N‘"=0;
~
xn
Q)Qh=20
Q\” =40
q=ti0`M
w JÌ4
=10(2+2,)
.
yl)=0
9
;M_
Ẫ
|
| Pa 20KN
lo,
z
\
E
14
Z,
Hình 1.18
; My” =-60
3) Về các biểu đồ:
Dựa vào các hệ thức (l) + (4) ta vẽ được biểu đồ như hình vẽ.
4) Kiểm tra sự cán bằng của núi:
Ở đây ta chỉ cần kiểm tra sự cân bằng của nút B.
Tách nút B bằng các mặt cắt sát nút a-a; b-b. Đặt các
ngoại lực và nội lực vào nút (hình I.L9), ta có:
>Y =65 - 25 - 40 =0
~m,
:
|
=60-60=0
Suy ra nút B cân bằng.
¿o ¡2
“
| ý
⁄/
\
60
Ny,
Wy
|
Mà"
WLLLLLLLLLL LALLA
V_=65
DA
l2
Hình 1.19
}7
BÀI TẬP LỚN SỐ 2
ĐẶC TRƯNG HÌNH HỌC CỦA HÌNH PHẲNG ˆ
_ SƠ ĐỔ A: Cho hình phang như hình 2.1. Hãy xác định các mơimen
qn tính chính
trung tâm của hình phẳng.
Số liệu: b = l6cm:h = 24 cm.
|
Bài giải:
l1) Xác định hệ trục quán tính chính trung tâm:
+ Chia hình phẳng thành 3 hình:
- Hình (1) là hình chữ nhật. ˆ
- Hình (2) là nửa hình trịn.
- Hình (3) là hình tam giác khuyết.
Hệ trục qn tính chính trung tâm của các hình tương ứng như (hình 2.1) Ta có:
+
|
| Y =y¡ =y2 =y; là trục đối xứng.
F,=b,h,
= 16.24=384 cm’
bjh;
12. 4'
j=l
= 12.24
12
12
= 13824cm*
b
Jy = JY = nib; _ 24-16
12
e
2
3
= 8192 cm
12
|
2
2
F, =xnR> =-3,14.8- =100 cm
2
3) =
1
,
_đ
2
4Ê
lr-
8
|
4
_ TR
Hi nGC
On
4
2
ơ
|-
8
of
9.314-
|
3,14. 4
|
|
3148
= 1608 em”
Ì
|
5
b,h, =— -12.12 =72cm2.2
FF, =—
|
“23
ji 3 = "36
DU
|
Tủ) = Ji
|
2
123
1212"_ _ 576 cm”
=2 [h8
3\
°
J3
163
: =
—
uc
= 432 cm*
F=F,+F;-F,=
384 + 100 - 72=412
cm -
18
= 448 cm!
+ X4c dinh trong tam C cua hinh phang trong hé (O,x,y,): vi y, = y là trục đối xứng
của hình phẳng nên í 's( y)).
yi
vk
S,
=a
Se Sh +8
AL
_
*
=
}
3}
op
.
WỦ%
r ay
Kio
0+ (12 + 3,4)| 100 -(-8).72
ee
fo
é
⁄
¬
é
4:2
= 3,1 crn
“5b_= 8cm
Xo
3R
_
m4
-
h_
5=
4.
12cm
sa
5,1cm
— Xj
ho
2” 12cm
—Xa
4cm
2c
—
Ob/4 = 1 2cm
2cm
b = 16cm
Hinh 2.1
19
+ Lập hệ trục quấn
tính chính
trung tâm CS
thì tọa độ trọng tâm
O,,
O, , O
ca
cac
“Ẳy,=—5/1 em
mm
H
2) Tính các momen quan tinh chinh trung tâm J
FSI
aI FIO =
+ yy
`.
Ho
4
- ix:
>
[x, =0
“mNemes”
hình trong hệ trục này là:
Jy:
+ I + y3 Fy) <0 + y3 Py)
= 13824 + (— 5,1) .384 + 448 + (10,3)”.100 - (576 + (-13,1)°.72) = 21 937 em?
Jý =J) +S - J) = 8192 + 1608 - 432 = 9368 cm?
Dap so: J, = 21 937 cm"
J, = 9368 cn”
SƠ DO B: Cho mat cat nhu hinh 2.2. Hay tinh cac momen quan tinh chinh trung tam
của mặt cắt bằng giải tích và đồ thị.
_
:
So liéu: [| N°20a; L N2200x 125x 16.
Bai giai:
1) Xác định trọng tâm của mặt cắt:
|
Chia mat cat thanh 2 hinh: Hinh (1) 1a | N220a:
bảng số liệu ứng với các mặt cắt nay:
| N®20a : h, = 20 cm;
Zo = 2,28cm;
_LN®200x125x16 -
h,= 20cm;
hình (2) là L N°200x 125x 16.
bị =8 cm;
d¿=0,52cm;
J,,=1670cm*;
J,, = 139 cm’.
b,=12,5cm;
F,=25,2cm'
d,=1,6cm:
F›=498cm;
x,=2,99cm;
y, =6,71 cm;
Jxo = 2026cm";
J, =617cem*;
Jy = 367 cm’.
Tra
|
Trong đó: trọng tâm các hình va hệ trục qn tính trung tâm của mỗi hình như (hình 2.2).
Ta sẽ tìm vị trí trọng tâm C(x,.; y,.) của mặt cắt trong hé O,x,y,. Ta co:
Vic =
S
xI
_ Sy
F
Sy =
X,=—
_F
tổn va —
F, + F,
Sy t+ SYP
H + F;
= C (3,5cem ; - 2,18cm).
20
=
=
0+-|
h,
2
9.
.
_ ~(10—6,71) 49,8.
JF
= —
F, + F,
OF (x, +2,)F,
3
H+F;,
-
=
25,2 + 49,8
(2994228) 408
:
25,2 + 49,8
= —2,18cm
= 3,5cm
Lập hệ trục trung tam (Cxy). Toa dé cua O,, O, treng hệ (Cxy) là:
[x
= -3 53CM
-
Jia = = (2094 2,28) -35= 17 7em
Iv, = 2Z,)6cm
lu
6
N20
hy
\
v
{
“
|
4 \ :4
AAR
4
|
re
&
N
200 x 125 x 16
⁄
xem
d
Ha
\
7
le
Gy=17 31"
fan
-
|
Z,72,28
=f
U=max
Xị
NI
b,= 8
4
2.1000cm „_
LO TTTT
21
2
1 No
=
——T TI
NNo
ft
4 dụ
NY :
35
“i}
ly: =~(10=6,/1~2,lã}= —Íjl lcm
\
X,=2,99
b=
aad
x
3877]41728
Jy
12,5
Hinh 2.2
2) Tính các momen qn tính cua mat cat đối với hệ trục trung tâm:
Cxy: J, Jy Sy
|
«J =J(1+ 12 = (st +y;F,)+ (J + y3F,)
= 1670 + (+ 2,18) .25,2 + 2026 + (—l,11)°.49,8 = 3877cm"
oJ, = 300 432) =
|
—
4x3 F)+ (Q9 +x‡E;)
=139+(-3,5).25,2 + 617 + (1,77) .49,8 = 1221 cm!
1"... = Gần +xiyF)+09, +X2¥2F2)= JO), - 290
Tinh Joy:
(1)
|
|
Ta có: lở = Syn =
Suy ra: JY 32 =
Jno tJ.
|1.
5
cổ Sax Iya)? + 4S gay,
du —142)0ys =2)
¬————
e
2l
Dấu của (2) được xác định nhờ vòng tròn Mo
quán tính. Trung trường hợp này ta thay:
|
T2 <Ư (hinh 2.3) nên:
:
Is
x2y2
|
VÀ KJ x2NĨ
— —
u?3)
(Jy
——
{J
x?
~
J u2
)
(J
y2
_
J u2
)
a
No»
y
/⁄
)
:
A
—
bu
AN
⁄
VU
{
=
TT đụ
|
\
—
Nf
NV
TLIELLALLLE
cm?
--644
5
=
⁄
Cri
U9
\
~i,
.
xay.
Thay vao (1):
|
Hình 2.3
J,y = - 644 - 290 = — 934cm"
3) Xác định hé truc quan tinh chinh trung tam C,,, va tính các mơinen qn tính
chinh trung tam J,, J,:
a) Bang giai tich:
Ta có: tg2œ, =—
"
23,
dS, AS
|
|
=—
2.(-934)
= 0,703
3877-1221
=> 2a, =35°02' => a, =17°31'; a, =a, +90° =107°31
Juyạ, =
JI, +J,
= un
5
5
+ - J0, =1) +42,
mi + < (3877-1221) + 4.(-934)? = 4172.6 cm! =J,
Senin = (Jy +I.) — Imax = 3877 + 1221) — 4172,6 = 925,4 cm! = J,
b) Bang do thi:
- Lay hé truc OJ,J,,
- Chon ti lé xich: 2cm ~ I000cm”
- Lấy điểm E(3877, 0) ; F(1221, 0); cực D(1221, - 934)
- Vẽ vòng tròn tâm C ở giữa EF, bán kính R = CD.
= Vong tron Mo quan tinh.
- Từ đồ thị:
Jax =Jy =1000- =
~ 41726 cm”
Jnin = Jy = 1000 . s ~ 925,4 cm”
Đáp số: œ¿= 1731
Jạ= Fos = 4172 6cm'
J,Vv =
22
J min
= 925,4cm’.
BÀI TẠP LỒN SỐ 3
a’
TÍNH BĐA¬M TIẾP
SƠ ĐỒ A: Cho dầm thép; có mặt cãt ngang gồm22 2 thép cl hu phép lại, chịu lực như hình 3. La.
Hãy chọn số liệu thép nêu [ơ] = 16 kN/cm'.
Sô liệu:
a=
Im;
k,=2;
P,=20kN;
P,=40kN;
k=l;
qg=12kN/m:
= M,=30kNm;
M,=20kNm.
Bai giai:
1) Chon so bộ mặt cắt đầm theo tái trong:
+ Vẽ biểu đồ nội lực do tải trọng gây ra:-@);
©);@)
- Tir diéu kién cân băng của dầm AB ta suy ra:
V`=45kN;
Vp =SIKN
- Dua vào sơ đồ ngoại lực tác dụng ta vẽ được các biểu đồ nội lực€3
2
như hình 3.I.
- Từ biểu đồ = Q!„„„ ==5 kN,ML.... =76 kNm = 7600 kNcm.
+ Chọn sơ bộ mặt cắt dầm theo tải trọng:
W,
.
— 2W?
,
—
M
I
nay
—
7600
[Ø]
=- 475
cm?
16
=> W,” = 237,5cm’.
| Tra bảng thép, ta sơ bộ chon [ N°24: W£'
Ji) = 2900 cm
= 242 cm *
; SẼ = 139 cm: '; at) = 0,24 kN/m ; h = 24cm ;d = 0,56 cm; t= lcm.
2) Kiểm tra lai các điều kiện bên cho dâm khi có kể đến trọng lượng dâm:
q, == aq?
= 0,48 kN/m.
+ Vẽ biểu đồ nội lực cho dầm
có kể đến trọng lượng đầm:
Vụ =45,96 kN ; Vạ= 51,96 kN.
Các biểu
đồ 6) ; M
được vẽ như hình 3.2.
Từ biểu đồ — Q. . . ymax = 51 96kN;- Mu„„„ =77kNm= 7700 kNem
—————————————~.
23
+ Kiểm tra lại các điều kiện bền cho dầm:
au) Kiém tra cho phân tổ ở trạng that tig suat don:
- Tại mặt cắt E có M,.... = 7700 kNem
Oo
M
_
max
=
max
_
VN
7700 = 15,9kN/em? <
~~
fo]= 16kN/em?;
2.242
eet
= honed
b) Kiém tra cho phan té truot thuan tuy:
- Tại mặt cat Bcé Q,,,,, = 51,96 KN.
P,= 20kN
8)
Z
A
— |V,z45kN
F
7
tty
YY
a=†m
Ch+1 AL =30kNm
|
P„=40kN
|
q=12-_
|
-kạa= 2m
ON
M,=20kNm
:
yo
—
|
kạa= 1m
1,08m
|
“mm.
©
13
11
|
H>
I
sự
) yy
We
sử
N
39
ý
j
1
LT
LLL
xứ)
Hình 3.1
+
|
Va=B1kN|
33
it,..
_
a
l
P,= 20kN
|
LEP
A1
?
í
?
Y
f
i
?
ơ
F=40hẹN
t |
tHjI !t!?tt
M;=30kNm
7
í
Y
|
}
tt:
chy
a=m
dE
k,a= 2m
'
ô26,48 s"
í
yơ
tỡ
ti
LD
M;=20kNm
tet
et
|
y
V,=51.96KN|
45,96
TT
_
33,48
13,48
-
J
|
ơ
51,95
|
:
|
|
11,4
qt
â)
51,48/
NQ
7
Su
5172
69,72/
|
N
TT/
Hỡnh 3.2
Una
x
max
Qinaxd,
..
=JO
x .b.
=
51,96 .2.139
| .
2.2900
2 . 0,56
|
_
Tính [t| theo thuyết bền thế năng biến đổi hình dáng lớn nhất:
16
It] =|o]/V3 = Te
9.25 kN/cm” 2
¬
Suy ra: 1, „. = 2,2 kN/em? < [tt].
3
,
= 2,.2kN/cm"|
to
:
T
kạa= 1m
1,08m
-|V,=45,96kN
Z
sở
g =12-4=
\
L
tổở trạng thái ng
tra cho phán
C) Kiểm
suat plang dac bret:
cd: Q, = SL48 KN SM, = 7172 kNem.
- Tai mat cat
- Chon phan tố K tiếp giáp giữa lòng và để những thuộc lòng.
[2
G, _=yo,
12,2
+3.t,
Slo]|
Tinh ơ, ; tị:
Oo, k
t,
=
‘VY,k
J,
Soc
x.
Q, si
=— _
bự
y
X
Q..1S.
y
.
_¢
x
=
|
|
2
hs
51,48.
|
2\2
=—
J,d
—
|
2.139— 70°
2
.
2
a4
\2
2.2900.2.0,56
|
= 1,8 kN/cm’
_=ơ, =vø +3-t¿ =((3/6)2 +3.(18)2 = 13,9kN/em? <[o] = I6kN/em”.
= Điều kiện bền cho đầm thỏa mãn.
3) Kế luận- Chọn 2 [ N°24..
SƠ ĐỒ B: Từ điều kiện bền và điều kiện cứng cho dầm hãy xác định giá trị tải trọng
cho phép tác dụng trên dầm.
Số liệu:
a=Im;
kị=l;
kạ=2;
IN® 20a ;
P,=2qa;
P,=3qa;
M,=6qa;
M;= 2qa ;
_Jø]= l6 kN/cm';
1"
E = 2.10°kN/cm’.
Bai giai:
1) Tinh dac trung hinh hoc:
Tra bang J N°20a: h=
20 cm
|
;
_ = 2030 cm” ;
h
2) Xác định [q] theo điều kiện bên:
+ Vẽ các biểu đồ nội lực
x
2
äđ=0 52cm;
t=0,56 cm ;
W, = 203 cm’ ;
S. = 114 cm’.
,
(hình 3.3)
Q,ạ„„ = 6qa = 6q kN
M,.„„ = 10.q.a” = 10.q.1.10° =q .10° kNem.
+ Xác định sơ b6 [q],:
ơ
Max
-
Suy ra: [q]y = 3,25 kN/m.
26-
|
P,=2qa
G)
P;=3qa
ro
(2)
—.
⁄
VỊ
:
/
dÝNN,,
N 0202
BUNS
§
kạa= 2m
|
Va=fae
len
6qa
2
|
4ga || |
TTS
UT
|
2
@
|
/
`
|
AUTH
NT
|
SUH
Le
|
A
| 2
—
AT TT]
ý
pe
10qa/⁄| lý
VY
y
y
⁄
⁄
VY
⁄
y
⁄
a
Hình 3.3
+ Kiểm tra bền lại toàn dầm:
a) Kiểm tra phân tố trượt thuần túy:
Tmax
_
Q naxx
J,d —
_
6:3,25.1
14
_ 21
kN/cm'”
< [+]
2030.0,52
— lơ]
— 925
kN/cmFˆ
7
v3
b) Kiểm tra phân tố ở trạng thái ứng suất phẳng đặc biệt:
- Chọn mặt cắt kiểm tra là D có:
Q, = 4qa = 4.3,25.1 = 13 kN
M, = I0qa? = 10°.3,25 = 3250 kNem.
27